双向正交密加筋板的极限强度预报

邱继栋 杨 平

武汉理工大学交通学院，湖北武汉430063

双向正交密加筋板的极限强度预报

邱继栋 杨 平

武汉理工大学交通学院，湖北武汉430063

采用数值分析方法，对一系列单轴受压的双向正交密加筋板进行了有限元非线性计算。基于有限元数值计算结果和正交异性板理论，引入纵向加强筋的柔度λx、横向加强筋的柔度λy以及密加筋板的柔度β这3个参数变量，提出了关于这3个参数变量的双向正交密加筋板极限强度预报公式。对3种类型加强筋的双向正交密加筋板的极限强度分析结果表明，预报公式结果与有限元计算结果的绝对误差很小，能准确预报双向正交密加筋板的极限强度。

双向正交密加筋板；有限元非线性分析；极限强度公式

0 引 言

随着船舶的高速化和轻型化以及高强度材料的运用，在满足安全性和适用性要求的前提下，优化船舶结构是控制空船重量的重要因素，并且结构重量的控制也成为设计成败的关键之一。减小板的厚度对减轻船舶结构重量效果显著，但由此也会引起板的局部强度、稳定性、局部振动性态的下降以及焊接变形的增大。因此，一种新型的船体加筋板结构形式——双向正交密加筋板被应用于高速船舶结构中。

双向正交密加筋板就是在甲板、船底、舷侧结构中，在相邻的纵向强力构件和横向强力构件为周界的板上，沿着纵向和横向分别设若干正交加强筋的一种结构形式。双向正交密加筋板的纵向长度L为横向强力构件的间距，横向长度B为纵向强力构件的间距，双向正交密加筋板是在L×B的尺度范围内布置纵、横骨材。双向正交密加筋板结构可以综合处理船体重量以及强度、刚度、振动、工艺等诸种矛盾，较大幅度地减轻结构重量［1］。

Kumar等［2］选取了 6块密加筋板，对受到轴向和横向载荷的正交加筋板的极限强度分别进行了实验研究和有限元分析，但没有提出能够广泛应用的双向正交密加筋板极限强度的预报公式。Paik等［3］对于受到双轴向压力和横向压力并且具有大挠度的正交密加筋板，将其转化成正交异性板，通过求解发生大挠度的正交异性板的非线性微分方程，推导出了其极限强度公式。Mikami等［4］基于正交异性板的理论，对受到单轴向压力的正交加筋板，提出了预报其极限强度的方法，该方法考虑了加筋板发生整体屈曲和纵向筋发生屈曲对极限强度的影响。

在我国的相关研究中，张征波对内河高速船双向密加筋板船体结构进行了试验及计算分析，为制订相关规范条款提出了建议。杨平和刘彦峰［5］对密加筋板结构进行了稳定性分析，推导出了单向受压密加筋板结构整体失稳时临界载荷的实用计算公式。

目前，双向正交密加筋板结构已成功应用于排水型高速船，在船舶性能上和经济性上获得了很大的效益。因此，对双向正交密加筋板结构进行进一步的理论研究具有很大的现实意义。

本文将运用有限元分析软件ANSYS，对单轴受压双向正交密加筋板的极限强度进行系列有限元非线性数值计算与分析，并将引入纵向加强筋的柔度λx、横向加强筋的柔度λy以及密加筋板的柔度β这3个参数变量，并提出了关于这3个参数变量的双向正交密加筋板的极限强度预报公式。

1 有限元非线性计算

1.1 计算模型的几何要素

本文中双向正交密加筋板的加强筋类型分别选取为扁钢、角钢、角钢/扁钢组合3种形式。结合实船情况，密加筋板的纵向长度取为 L=1 800 mm，长宽比取为 L/B=0.8，1.0，1.2，1.5，1.8，2.0。对于相同长宽比的加筋板，其板厚分别取为3，4，5，6 mm。对于相同长宽比并且相同板厚的加筋板，加强筋数目分别取为3×3，3×4，4×4和4×5。纵向和横向加强筋的几何尺寸如表1所示，双向正交密加筋板的几何模型如图1所示。

1.2 有限元非线性计算模型

计算模型采用4节点、6自由度的SHELL181单元，假定材料弹性为理想塑性，并忽略材料的应力强化作用，以von Mises屈服准则作为材料的屈服准则。杨氏模量 E=2.0 6×105MPa，材料屈服极限 σy=315 MPa，泊松比 ν=0.3。计算中考虑双向正交密加筋板的初始变形，以其1阶屈曲模态作为初始变形形状［6］，板的变形幅值和加强筋的变形幅值分别取为wopl=0.1β2t和woc=0.001 5L。

表1 纵向和横向加强筋的几何尺寸Tab.1 Longitudinal and transverse stiffener sizes

图1 双向正交密加筋板几何模型Fig.1 A typical two-way orthogonal multi-stiffened plate and its geometric parameters

对于双向正交密加筋板，焊接残余压应力会降低极限强度，但因焊接残余拉应力对增强极限强度有贡献，两者对极限强度的影响大致相互抵消，因此本文不考虑焊接残余应力。偏于安全考虑，计算模型的边界条件取为简支。

图2所示为加强筋数目为ny×nx=3×4，扁钢加强筋双向正交密加筋板的有限元模型。

图2 双向正交密加筋板有限元模型Fig.2 Nonlinear finite element model of two-way orthogonal multi-stiffened plate

1.3 有限元非线性计算结果

图3～图5分别给出了加强筋为扁钢、角钢、角钢/扁钢组合的双向正交密加筋板极限强度与板厚的关系图。

图3表明，对于扁钢加强筋的双向正交密加筋板，当板厚和加强筋的数目一定时，极限强度随长宽比的增大而增大。

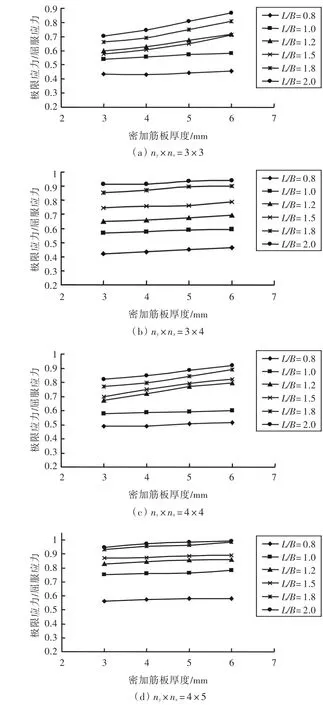
图3 扁钢加强筋密加筋板的极限强度(σu/σy)与板厚的关系图Fig.3 The ultimate strength versus thickness of multi-stiffened plate with flat bar

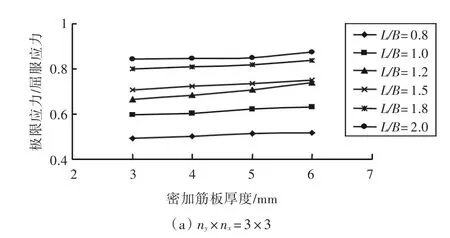
图4 角钢加强筋密加筋板的极限强度(σu/σr)与板厚的关系图Fig.4 The ultimate strengthversusthickness of multi-stiffened plate with angle bar

图4表明，对于角钢加强筋的双向正交密加筋板，当纵、横向加强筋数目及长宽比相同时，板厚对极限强度的影响变化不大。而当纵、横向加强筋数目不同时，长宽比对极限强度的影响变化较大。

图5 角钢/扁钢组合加强筋密加筋板的极限强度(σu/σr)与板厚的关系图Fig.5 The ultimate strengthversusthickness of multi-stiffened plate with flat bar and angle bar

图5表明，对于角钢/扁钢组合的双向正交密加筋板，当板厚一定时，长宽比对极限强度的影响逐渐变小。

图3～图5表明，对于不同加强筋形式的双向正交密加筋板，当加强筋数目一定时，其极限应力随着加筋板板厚的增加而增大。在实船设计中，若采用本文所取的3种加强筋形式的双向密加筋板，并且所取板厚一定，便可根据图3～图5选择合适的长宽比。

图6给出了加强筋分别为扁钢、角钢、角钢/扁钢组合的双向正交密加筋板关于不同长宽比的应力应变曲线。

图6 双向正交密加筋板关于不同长宽比的应力应变曲线Fig.6 Stresses versus axial strains with respect to length-width ratio

图6表明，在弹性屈曲阶段，双向正交密加筋板的等效弹性模量不同，并且不同长宽比所对应的极限应力不同，长宽比越大，对应的极限应力便越大。对于角钢/扁钢加强筋双向密加筋板，其纵向与横向加强筋的截面形式差异明显，在弹性屈曲阶段，与角钢和扁钢加强筋双向密加筋板的等效弹性模量的大小相比，角钢/扁钢加强筋形式的变化要明显些。

2 双向正交密加筋板的极限强度预报公式

通过对船体加筋板尺寸进行分析统计，文献［7］确定了船体加筋板的相关参数，并且这些参数是影响船体加筋板极限强度的重要参数。

基于正交异性板的理论，对于双向正交密加筋板，引入了3个参数变量［8-9］，即密加筋板的柔度β，纵向加强筋的柔度 λx和横向加强筋的柔度λy。在大量有限元非线性计算的基础上，对加强筋为扁钢、角钢、角钢/扁钢组合的双向正交密加筋板，分别拟合出了其相应的极限强度预报公式。

加筋板的柔度：

纵向加强筋的柔度：

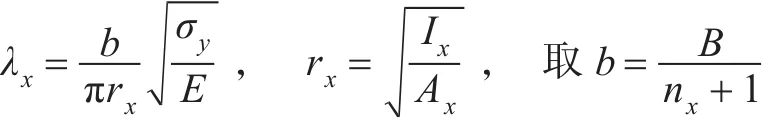
横向加强筋的柔度：

式中，L，B分别为双向正交密加筋板的纵向长度和横向长度；nx，ny分别为纵、横向加强筋的数目；Ax，Ay分别为纵、横向截面面积；Ix，Iy分别为纵、横向加强筋关于中性轴的截面惯性矩；rx，ry分别为纵、横向加强筋的惯性半径，在计算rx，ry时，带板宽度分别取为b，a。

本文提出双向正交密加筋板的极限强度预报公式的表达形式为：

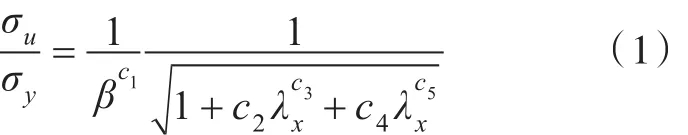
其中，表达式系数c1～c5依据非线性有限元计算数据确定。

依据非线性有限元计算的双向正交密加筋板极限强度的数据，采用麦夸特法（Marquardt）算法［10］进行非线性回归，得到不同加强筋形式的双向正交密加筋板极限强度预报公式。

对于本文所取的扁钢加强筋、角钢加强筋、角钢/扁钢组合加强筋的双向正交密加筋板，极限强度预报公式分别为：

3 双向正交密加筋板极限强度分析

3.1 扁钢双向正交密加筋板极限强度分析

图7给出了扁钢加强筋双向正交密加筋板极限强度的公式计算值与有限元计算值之间绝对误差的分布。

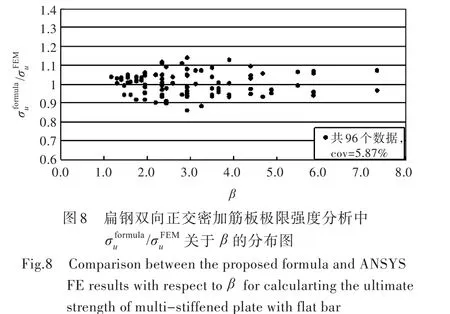
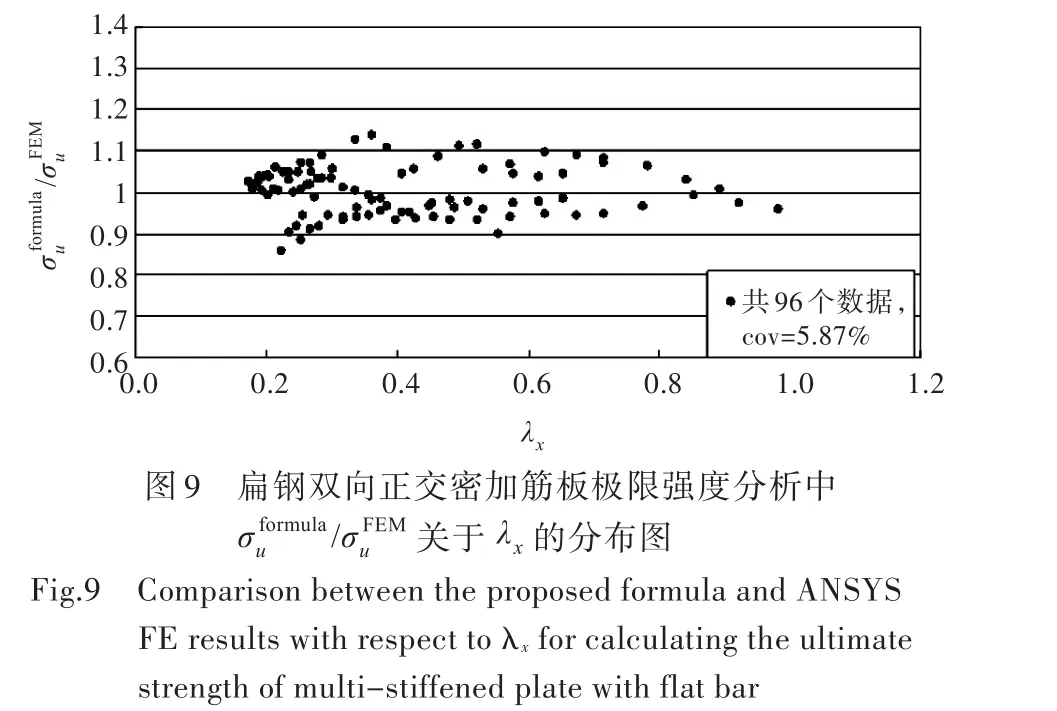
图7中横坐标为公式计算值与有限元计算值之间的绝对误差，纵坐标为绝对误差的概率分布。由图7可得出，有限元计算值与公式计算值之间的绝对误差基本小于10%，有69.7%的绝对误差在－5%～5%之间，公式值与有限元之间的标准差为4.19%，平均误差为0.06%，数据变异系数（cov）为5.87%。

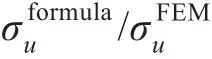
图7 对扁钢双向正交密加筋板极限强度分析中公式计算值与有限元计算值之间绝对误差的分布图Fig.7 Comparison of error bands between the proposed formula and ANSYS FE results for calculating the ultimate strength of multi-stiffened plate with flat bar

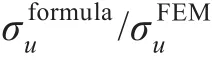
3.2 角钢双向正交密加筋板极限强度分析

图11给出了角钢加强筋双向正交密加筋板极限强度的公式计算值与有限元计算值之间绝对误差的分布。

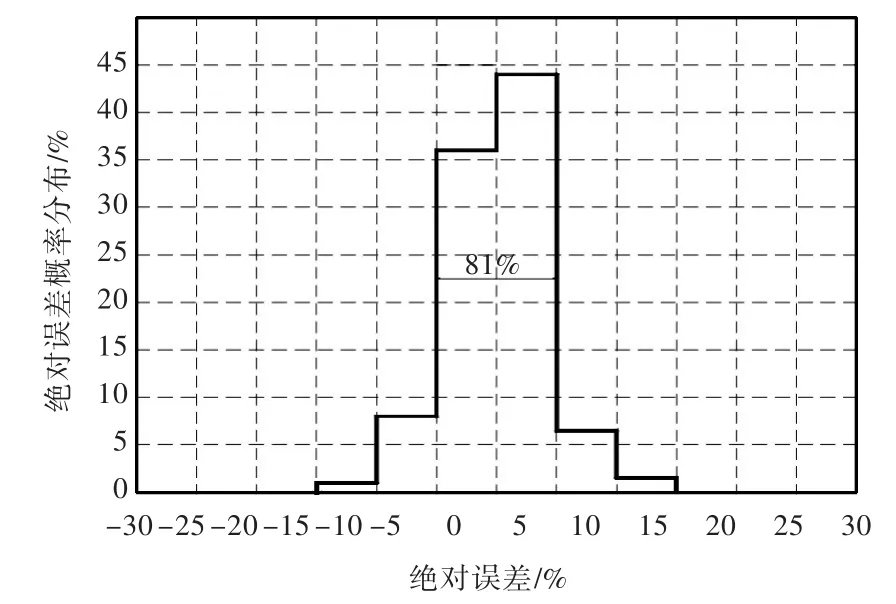
图11 角钢双向正交密加筋板极限强度分析中公式计算值与有限元计算值之间绝对误差分布图Fig.11 Comparison of error bands between the proposed formula and ANSYS FE results for calculating the ultimate strength of multi-stiffened plate with angle bar

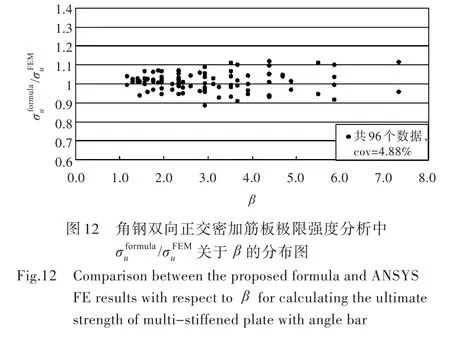
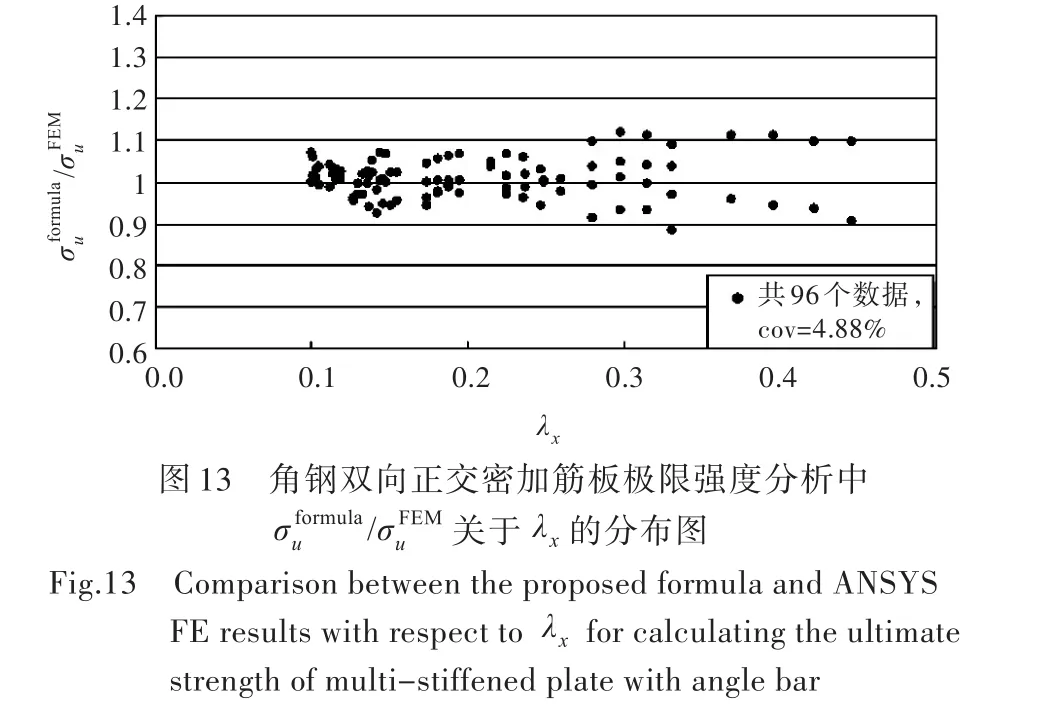
由图11可得出，有限元计算值与公式计算值之间的绝对误差均小于15%，有81%的误差在－5%～5%之间。通过计算得到，公式值与有限元之间的标准差为3.49%，平均误差为0.06%，数据变异系数（cov）为4.88%。

3.3 角钢/扁钢组合双向正交密加筋板极限强度分析

图15给出了公式计算值与有限元计算值之间绝对误差的分布。

图15 角钢/扁钢组合双向正交密加筋板极限强度分析中公式计算值与有限元计算值之间绝对误差分布图Fig.15 Comparison of error bands between the proposed formula and ANSYS FE results for calculating the ultimate strength of multi-stiffened plate with flat bar and angle bar

由图15可知，有限元计算值与公式计算值之间的绝对误差均小于10%，其中有91.7%的绝对误差在－5%～5%之间。通过计算可知，公式计算值与有限元之间的标准差为4.16%，平均误差为0.05%，数据变异系数（cov）为5.04%。

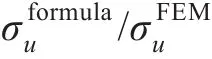
4 结 论

通过引入纵向加强筋的柔度λx、横向加强筋的柔度λy以及密加筋板板的柔度 β这3个参数变量，提出了关于这3个参数变量的双向正交密加筋板极限强度预报公式。

分别用有限元计算软件和所提出的预报公式分析了扁钢、角钢和角钢/扁钢组合这3种类型加强筋双向正交密加筋板的极限强度，预报公式结果与有限元计算结果之间的绝对误差很小，能准确预报双向正交密加筋板的极限强度。

［1］张征波.内河高速船的新型船体结构形式——双向加筋板船体结构［J］.船舶工程，2004，26（1）：22-25.

ZHANG Z B.A novel hull structure design for highspeed in land waterway craft-hull structure with stiffeners in two directions［J］.Ship Engineering，2004，26（1）：22-25.

［2］KUMAR M S，KUMAR C L，ALAGUSUNDARAMOORTHY P，et al.Ultimate strength of orthogonal stiffened plates subjected to axialand lateral loads［J］.Structural Engineering，2010，14（2）：197-206.

［3］PAIK J K，THAYAMBALLI A K，JU K B.Large deflection orthotropic plate approach to develop ultimate strength formulations for stiffened panels under combined biaxial compression/tension and lateral pressure［J］.Thin-Walled Structures，2001，39（3）：215-246.

［4］MIKAMI I，NIWA K.Ultimate compressive strength of orthogonally stiffened steel pates［J］.Journal of Structural Engineering，1996，122（6）：674-682.

［5］杨平，刘彦峰.密加筋板结构的稳定性分析［J］.船海工程，2006，35（6）：17-19.

YANG P，LIU Y F.Bulking analysis for the multi-stiffened plates［J］.Ship and Ocean Engineering，2006，35（6）：17-19.

［6］MANSOUR A，WIRSCHING P，LUCKETT M，et al.Assessment of reliability of existing ship structures［R/OL］.［2011-03-12］.http://dodreports.com/ada330933.

［7］ZHANG S M，KHAN I.Buckling and ultimate capability of plates and stiffened panels in axial compression［J］.Marine Structures，2009，22（4）：791-808.

［8］张晓丹，杨平.加筋板在轴向压力下的极限强度研究［J］.武汉理工大学学报（交通科学与工程版），2011，35（2）：305-308.

ZHANG X D，YANG P.Ultimate strength of stiffened plate under axial compression［J］.Journal of Wuhan University of Technology（Transportation Science and Engineering），2011，35（2）：305-308.

［9］PAIK J K.Empirical formulations for predicting the ultimate compressive strength of welded aluminum stiffened panels［J］.Thin-Walled Structures，2007，45（2）：171-184.

［10］张韵华，奚梅成，陈效群.数值计算方法与算法［M］.北京：科学出版社，2006.

Prediction on Ultimate Strength of the Two-Way Orthogonal Multi-Stiffened Plates

QIU Ji-dong YANG Ping

School of Transportation，Wuhan University of Technology，Wuhan 430063，China

Nonlinear FEM has been performed to a series of two-way orthogonal multi-stiffened plates subjected to axial compression load.Based on numerical results and orthotropic plate theory，we introduced three parameters，which were longitudinal column slenderness ratio λx，transverse column slenderness ratio λy，and plate slenderness ratio β ，to form a prediction formula to calculate the ultimate strength of two-way orthogonal multi-stiffened plates.Then the ultimate strength for three types of multi-stiffened plates was analyzed.The results show that the calculation data agree well with the results of finite element analysis，and the proposed prediction formula is able to accurately predict the ultimate of two-way orthogonal multi-stiffened plates.

two-way orthogonal multi-stiffened plates；nonlinear FEM analysis；ultimate strength formula

U661.43

A

1673－3185（2012）03－57－07

10 .3969/j.issn .1673－3185 .2012 .03 .011

2011－05－16

邱继栋（1983－），男，硕士研究生。研究方向：船舶与海洋工程结构物设计制造。E-mail：wuhanlgd_qjd＠163.com

杨 平（1955－），男，博士，教授，博士生导师。研究方向：船舶与海洋工程结构强度理论与计算方法、工程结构物的极限承载力。E-mail：pyangwhut＠163.com

杨 平。

［责任编辑：喻 菁］