I型金属夹层结构连接构件强度数值计算方法

王 虎 程远胜 刘 均

华中科技大学船舶与海洋工程学院，湖北武汉430074

I型金属夹层结构连接构件强度数值计算方法

王 虎 程远胜 刘 均

华中科技大学船舶与海洋工程学院，湖北武汉430074

激光焊接钢质夹层结构在国外已用于实船，其连接构件的强度特性是设计者关注的关键问题之一。应用有限元分析软件ANSYS，提出采用壳体连接技术和子模型法，对I型金属夹层结构的两种典型连接构件进行强度分析。通过与全部体单元模型计算结果进行对比，分析了多点约束、自由度耦合、约束方程和端面壳4种壳体连接方法和子模型法计算连接构件在面内、面外载荷作用下强度的计算精度。结果对比表明，在主模型网格划分合理的情况下，采用端面壳、壳—体多点约束的子模型法可取得较好的计算精度与操作简便性的平衡，同时，还可大大降低计算规模。

夹层结构；连接构件；子模型；壳体连接；船舶

0 引 言

夹层结构具有比强度高、抗冲击性能好、防腐、隔热、隔声和防辐射等优良性能，在船舶结构制造中有着广阔的应用前景［1-2］。有研究表明，I型金属夹层结构的应用可以使某船体结构的总质量至少降低34%，制造成本约降低50%［3］。连接构件形式的选取是夹层结构在船舶结构制造中应用的关键问题之一。连接构件形式不仅影响船体结构的组装工时，也在一定程度上影响夹层结构的强度和疲劳等力学性能。目前，关于I型夹层结构连接构件形式及其强度特性的研究尚不充分。

Pyszko［4］建立了一种典型连接构件的二维参数化有限元模型，分析了其在拉压载荷与弯曲载荷联合作用下极限承载能力随主要设计参数的变化规律，并得出最优设计方案。Niklas［5］建立了两种典型连接构件的参数化有限元模型，分析了其在拉压载荷作用下，最大von Mises应力与名义应力的比值随主要设计参数的变化规律，由此得出两种连接形式的最优设计方案，并进行了对比分析。以上两位学者均仅采用平面应变模型研究了面内载荷作用下连接构件的强度，而未充分考虑连接构件与夹层结构面板之间接触的影响。但在实际使用中，连接构件也需承受面外载荷。在面外载荷作用下，实际结构并不满足平面应变的假定，在有限元分析中需建立其三维模型。由于在连接构件焊接接头处存在应力集中，因此有限元模型需考虑到实际结构的局部细节。但如果整个计算模型全部采用体单元，计算规模又会非常庞大。

本文提出采用壳体连接的三维有限元模型，并应用子模型法，考虑连接构件与夹层结构面板之间接触的影响，分析连接构件在面内、面外载荷作用下的强度。通过与全部体单元模型计算结果进行对比，分析多种壳体连接方法和子模型法的计算精度。

1 I型夹层结构连接构件

目前，夹层板架结构常用夹层板格结构取代纵桁间的传统加筋板结构，同时保留纵桁与强横梁［6-7］，如图1所示。纵桁与强横梁可以作为夹层板格结构的刚性支持边界。实际制造时，I型夹层板格结构的宽度有限，有时不足以横跨纵桁和舷侧间距或相邻纵桁间距，此时，便需要用连接构件将夹层板格结构横向相连，如图2所示。

本文所研究的内嵌方框型和外接平板型连接构件如图3所示。I型夹层结构与连接构件的连接由传统焊接实现，I型金属夹层板格结构面板与腹板的连接由激光焊接实现。

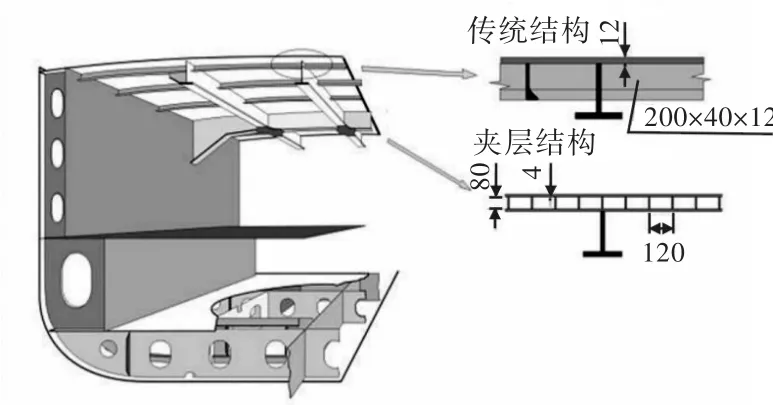
图1 夹层结构在船体结构中的应用示意图Fig.1 The application of sandwich panel in shipbuilding

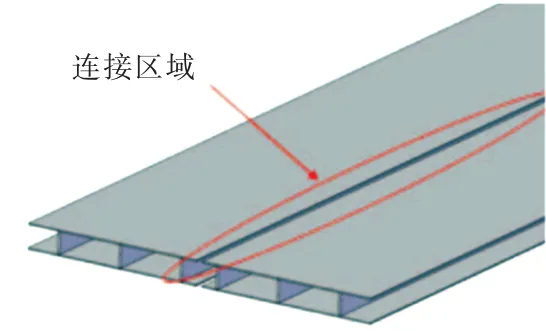
图2 I型夹层板格结构连接示意图Fig.2 Connection between sandwich panels

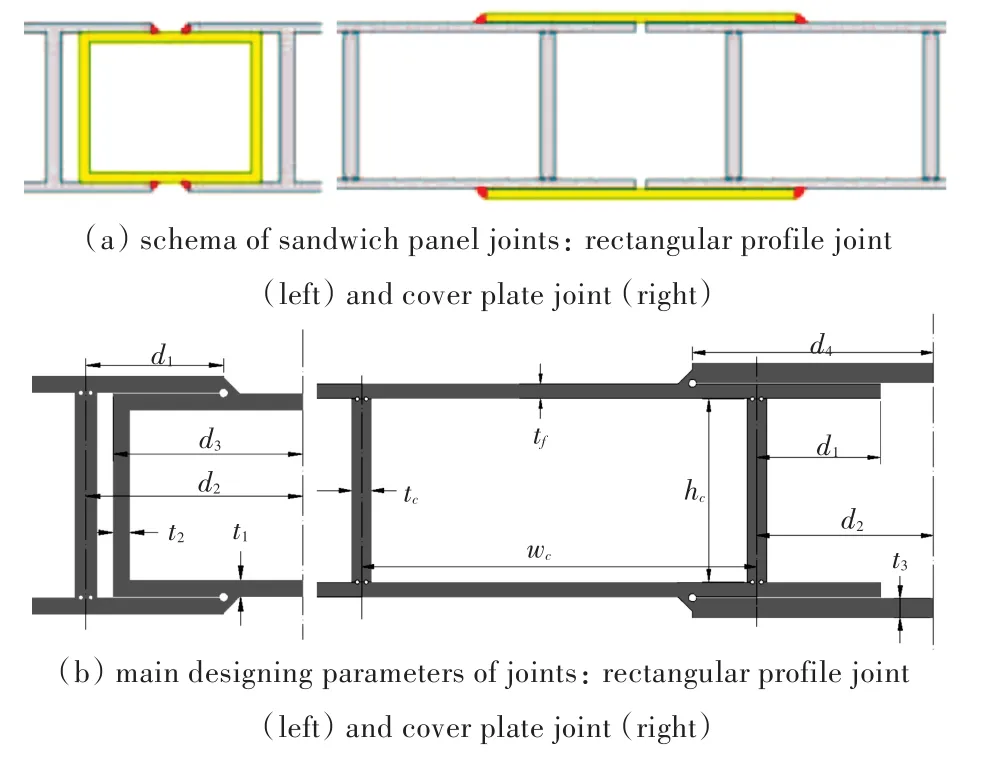
图3 连接构件及其主要设计参数Fig.3 Schema and main designing parameters of sandwich panel joints

2 分析方法

2.1 分析模型

本文取宽2.2 m、长1.5 m、中间含有内嵌方框型或外接平板型连接构件的夹层板格结构作为研究对象，将纵桁和强横梁作为其自由支持边界，分析其在面内均布载荷（取100 MPa）和面外均布载荷（取150 kPa）作用下的强度。

在面外载荷作用下，考虑到模型和载荷的对称性，取1/4整体结构作为分析对象，施加适当的对称边界约束。在面内载荷作用下，考虑到模型及载荷的对称性，以及远离连接构件的夹层结构部分对连接构件强度的影响甚小，采用仅含3根芯层腹板并仅取上层面板和芯层上半部分的结构作为分析对象，施加适当的对称边界约束。因为夹层板格与连接构件、面内载荷及边界条件沿长度方向没有变化，因而分析模型可简化为平面应变模型。但为了对比分析壳体连接模型的精度，尚需采用全部体单元建模，因此，面内载荷工况计算模型的长度取为10 mm（增加模型长度的系列对比计算可验证，该工况模型长度对计算结果的影响很小）。

2.1.1 全部体单元计算模型

在I型夹层结构与连接构件的普通焊接接头处，存在着应力集中。为了准确分析此处的应力分布，在建模时，需考虑此处结构的细节。普通焊接接头结构，以及实际夹层结构面板与腹板激光焊接接头均采用solid45体单元模拟，如图4所示。其他结构亦采用体单元模拟。这种全部采用体单元的计算模型的计算结果将作为后续各种简化模型精度对比分析的基准。整个结构全部采用体单元模拟时，其计算规模相当大，总单元数可达200万量级。

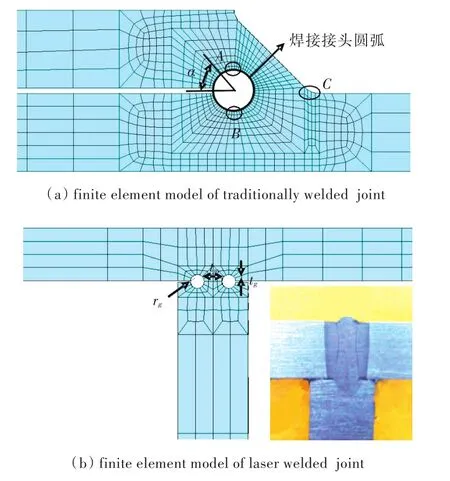
图4 全部体单元模型中普通焊接和激光焊接接头的有限元模型Fig.4 The finite element models of traditionally welded joint and laser welded joint in the model wholly meshed with brick element

2.1.2 壳体连接计算模型

上节中已说明普通焊接接头结构采用solid45体单元模拟。但当关注的是连接构件的强度问题时，鉴于激光焊接接头与普通焊接接头有一定的距离，其建模精细程度对普通焊接接头的应力状况影响相对较小，故可采用简化的壳单元模型模拟激光焊接接头（图5（a）所示）。对于普通焊接接头附近以外的夹层结构和连接构件，亦可采用shell63壳单元模拟。因壳单元节点与体单元节点的自由度数不同，故在普通焊接接头附近要进行壳体连接处理，如图5（b）所示。

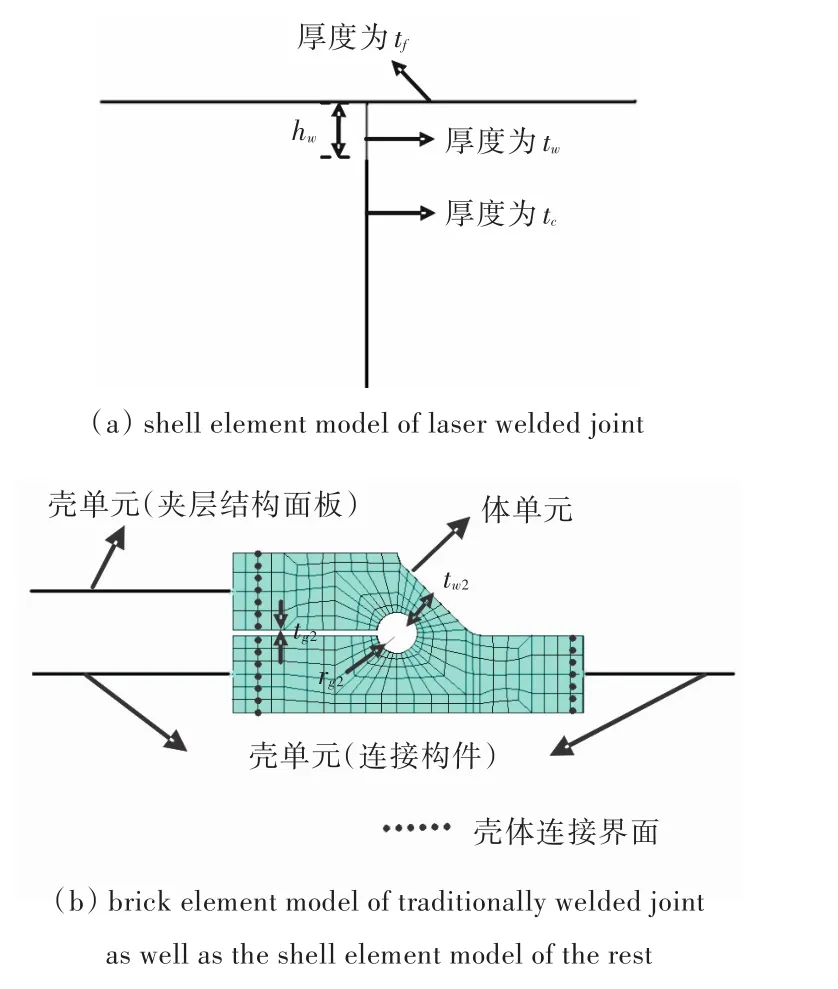
图5 壳体连接有限元模型Fig.5 The finite element model of shell-solid assembly

当用壳单元模拟I型夹层结构激光焊接接头时，面板厚度tf、腹板厚度tc、有效焊接连接宽度tw等参数均可根据实体模型确定（图5（a）），但hw的取值则需要由其他等效方法确定。本文采用如下方法确定hw的取值：分别用壳单元和体单元建立不含连接构件的I型夹层结构有限元模型，以全部体单元模型中，板格中点下层面板节点处沿受载方向的位移作为基准值，反推壳单元模型hw的取值，使壳单元模型对应点的位移值与基准值相同。在后续的面内与面外载荷工况计算中，hw均取1.0 mm。本文计算所用的夹层结构、连接构件及焊接接头的尺寸如表1所示。

2.2 子模型方法

2.2.1 子模型方法的原理及特点

再例如，有一篇文章，题目为“5 Ways to Just Enjoy retirement”。题目一目了然，看到这样的题目，听者心里便会放松许多，减少了许多盲目性。只要注意区分是哪五种享受退休生活的方式，并记下相关信息就行了。

子模型方法是一种用于在模型局部取得更准确结果的有限元分析技术［8］。在应用有限元进行大型结构的整体分析时，往往需要关注一些局部细节部位的应力分布。而如果对这些细节部位划分的网格较密，又会导致整体模型的计算规模过大，计算时间过长。此时，可以引入子模型方法。首先，建立局部细节部位网格较粗的整体模型，并予以分析计算；然后，再将整体模型中的局部细节部位切割出来，重新划分较密的网格作为子模型，并以整体模型在切割边界上的计算位移值作为子模型的边界条件再次分析计算，由此，便可得到更准确的局部细节部位的应力分布。

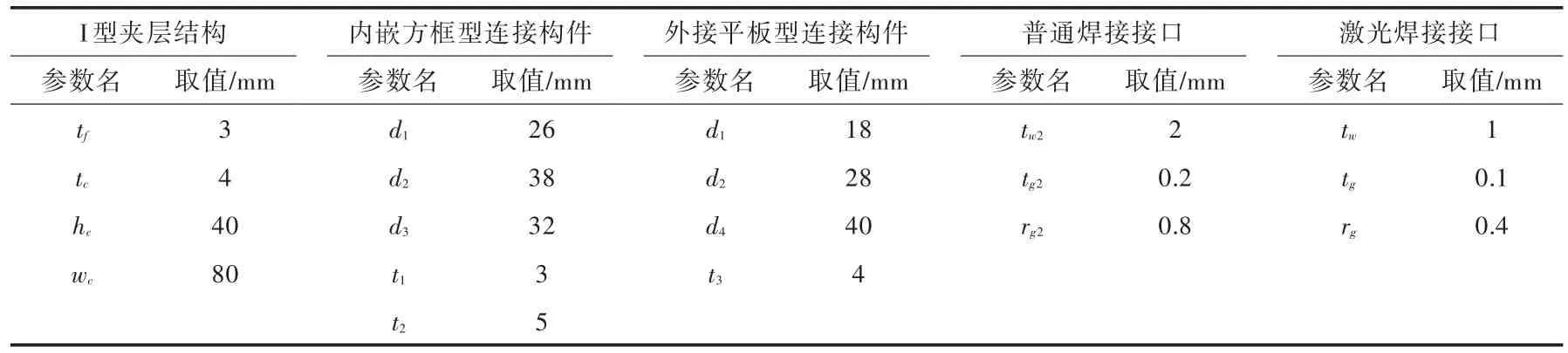
表1 主要设计参数及焊接接头尺寸取值表Tab.1 The values of main designing parameters and weld dimensions

子模型的特点在于，它减少甚至是取消了有限元实体模型中所需的传递区域，可以根据分析的需要，将所研究部位的网格划分得足够细，同时又不至于耗费过多的计算资源［9］。但同时也需注意，切割边界应远离应力集中、变形较大的区域，而且所切割的区域相对于研究的区域不能太小，否则，会影响计算的准确度［10］。

2.2.2 子模型方法的验证

分别针对内嵌方框型和外接平板型连接构件的全部体单元面内载荷分析有限元模型，逐步加密焊接接头处的网格。通过对比接头处的最大von Mises应力可见，1/4圆弧（图4（a））沿周向划分16个单元和32个单元的相对误差分别为3.20%和3.12%，因此认为网格已收敛，并将1/4圆弧沿周向划分16个单元的模型作为细网格完整模型。

为了验证子模型方法的正确性，先建立外接平板型连接构件的粗网格完整模型（1/4圆弧处周向单元数分别取 4，8，10，12，14），以此作为主模型进行分析计算，然后再用细网格的子模型（1/4圆弧处周向单元数为16，与细网格完整模型一致）通过切割边界计算局部应力，并与细网格完整模型的计算结果进行对比。在上述计算模型中，圆弧处径向单元数为周向单元数的一半。如图6所示，当主模型1/4圆弧处的单元数由4加密到14时，接头处最大von Mises应力的误差由3.9%减小到0.33%（图中，n为粗网格完整模型1/4圆弧处单元数；误差指子模型最大应力计算结果与细网格完整模型的误差）。对于内嵌方框型连接构件，也有类似的结果。可见，主模型的网格不能过粗，否则，也会引起较大的误差。

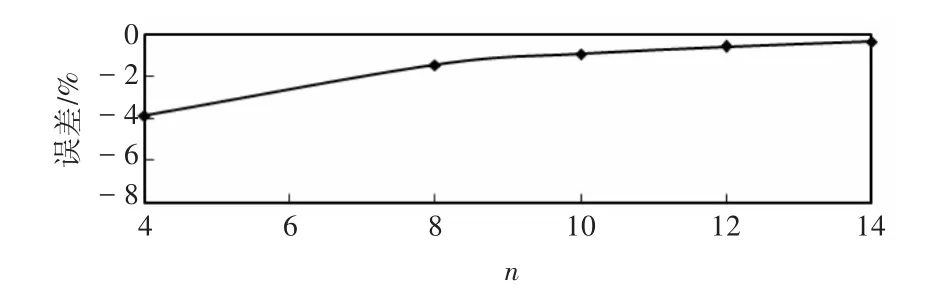
图6 不同网格下子模型局部最大应力计算误差Fig.6 Stress computational error of submodel under different mesh density

本文取1/4圆弧处周向单元数为8的粗网格完整模型（其接头处网格如图5（b）所示）作为主模型。对于内嵌方框型和外接平板型连接构件，其接头处的最大von Mises应力误差分别为1.63%和1.44%。粗网格完整模型接头处的单元数仅为细网格完整模型的1/5～1/6。

2.3 壳体连接方法

本文对比分析了4种壳体连接方法的计算精度，包括自由度耦合、端面壳（在连接界面壳单元厚度范围内创建端面壳单元，厚度可取壳单元厚度的ratio倍，然后合并端面壳单元节点、体单元节点和壳单元节点）、多点约束和约束方程（通过rbe3命令，将壳体连接界面上的壳单元节点定义为主点，体单元节点定义为从点，将主点的力和弯矩分布到从点上，从而定义壳单元节点和体单元节点之间的约束方程）。

2.3.1 面内载荷工况

以第3.2.2小节中细网格完整模型（1/4圆弧沿周向划分16个单元）的计算结果为基准，对比不同壳体连接做法连同子模型方法。在模型长度方向，对称剖面应力特征点 A，B，C（图 4（a））的von Mises应力和受载端部面板中面节点沿受载方向的位移精度如表2所示。

表2 面内载荷作用下不同壳体连接方法连同子模型方法的计算误差Tab.2 Calculation error of shell-solid assemblies together with submodel under in-plane load

表2的结果显示，自由度耦合方法的计算精度较差（在面外载荷工况不再考虑），这是因为此种连接方式只能传递力而不能传递弯矩。对于各种厚度的端面壳处理方法，应力与位移精度无实质性差异，端面壳厚度越小，位移越大。对于3种多点约束方法，应力的计算精度无实质性差异，但体—体约束方法的位移计算精度偏低，壳—体约束方法的位移计算精度最好。约束方程方法的计算精度也很高，但操作不便，需得到连接界面上所有节点的编号，然后再分主节点和从节点进行定义。

采用壳—体多点约束的子模型法计算得到的接头圆弧边缘（图4（a））的von Mises应力分布如图7所示。为便于对比，采用全部体单元细网格计算模型得到的对应结果也列于图7中。通过对比2条曲线可知，两者吻合较好。

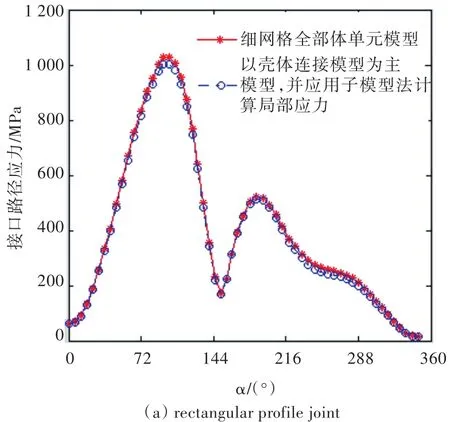
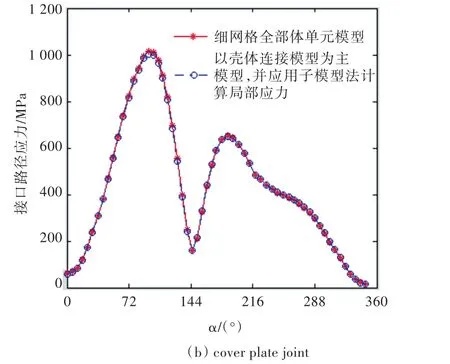
图7 面内载荷下采用壳—体多点约束的子模型法计算得到的接头圆弧边缘的von Mises应力分布Fig.7 Stress distribution along the circle obtained from the model of shell-solid assembly（shell-solid constraint option）together with submodel under in-plane load

2.3.2 面外载荷工况

以第3.2.2小节中细网格完整模型（1/4圆弧沿周向划分16个单元）在面外载荷下的计算结果为基准，对比不同壳体连接做法连同子模型方法。在模型长度方向，距对称剖面一定距离的截面上（此截面的应力要比对称面上的应力大），应力特征点A，B，C（图4（a）为上接头，下接头的3个特征点类似）的von Mises应力，以及板格中点下层面板节点处沿受载方向的位移精度如表3所示。

表3中的结果显示，对于各种厚度的端面壳处理方法，应力与位移精度无实质性差异，端面壳厚度越小，位移越大；对于3种多点约束方法，应力的计算精度无实质性差异，但体—体、壳—壳多点约束的位移误差约为3%，而壳—体约束方法的位移计算误差则约为1.3%。这是因为体—体、壳—壳多点约束均在连接界面创建了虚拟壳（与端面壳类似，且厚度为壳单元厚度），增大了模型的面外刚度，因而位移值偏小。而壳—体多点约束因没有在界面定义多余的壳单元，因而位移结果与基准值更接近，这与约束方程的处理方法类似。

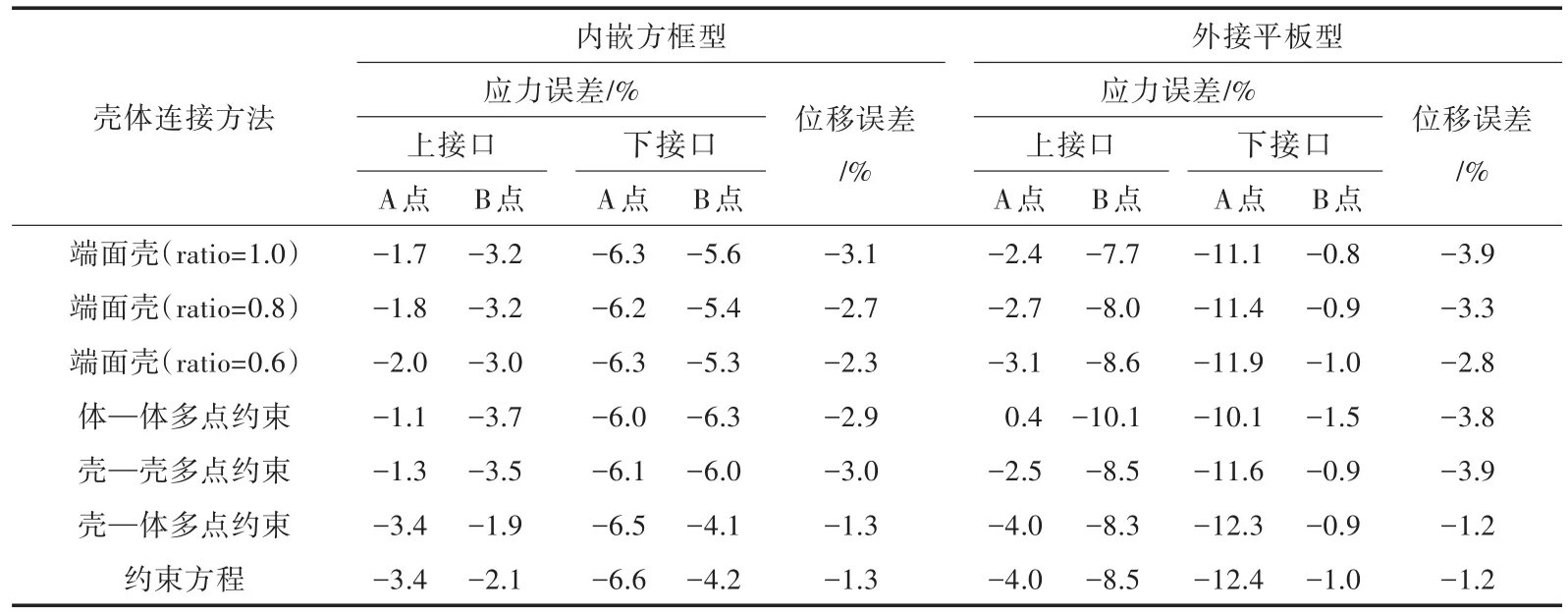
表3 面外载荷作用下不同壳体连接方法连同子模型方法的计算误差Tab.3 Calculation error of shell-solid assemblies together with submodel under out-of-plane load

在面外载荷下，采用壳—体多点约束的子模型法计算得到的上接头圆弧边缘（图4（a））的von Mises应力分布如图8所示。为便于对比，采用全部体单元细网格计算模型得到的对应结果也列于图8中。通过对比2条曲线可知，两者总体吻合较好，但外接平板型连接构件的精度稍差。通过与图7的结果进行对比可知，与面内载荷工况相比，面外载荷工况的计算精度较低。

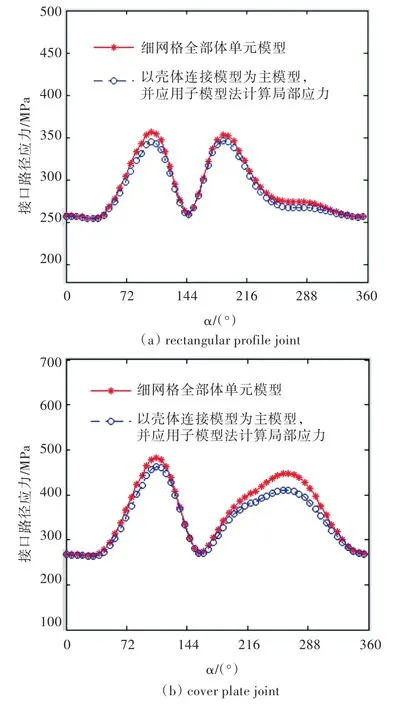
图8 面外载荷下采用壳—体多点约束的子模型法计算得到的上接头圆弧边缘的von Mises应力分布Fig.8 Stress distribution along the circle calculated by the model of shell-solid assembly（shell-solid constraint option）together with submodel under out-of-plane load

综合分析计算结果可见，壳—体多点约束方法的计算精度较好，通用性很好，且定义也相对简便。采用壳体连接和子模型的计算方法可大大降低计算规模，壳体连接模型（粗网格）的单元数仅为全部体单元细网格完整模型的1/10。

3 结 论

本文提出了采用壳体连接技术与子模型法相结合的I型金属夹层结构两种典型连接构件强度分析模型，通过与全部体单元模型计算结果进行对比，得到如下结论：

1）当关注连接构件的强度问题时，除连接构件焊接接头附近的结构采用体单元模拟外，其它结构，包括夹层结构面板与腹板激光焊接接头，均可采用壳单元模拟。

2）子模型法的计算精度与主模型的网格划分有关。一般当子模型的网格密度为主模型网格密度的一倍时，可取得满意的计算精度。

3）采用端面壳、多点约束和约束方程的壳体连接方法连同子模型法分析I型夹层结构连接构件的强度特性可以大大降低计算规模，并能保证较好的计算精度。考虑到操作的简便性，端面壳和壳—体多点约束的壳体连接方法可作为首选。

［1］METSCHKOW B.Sandwich panels in shipbuilding［J］.Polish Maritime Research，2006（s1）：5-8.

［2］KUJALA P，KLANAC A.Steel sandwich panels in ma⁃rine applications［J］.Brodogradnja，2005，56（4）：305-314.

［3］ROLAND F，REINERT T.Laser welded sandwich pan⁃els for the shipbuilding industry［C］//Lightweight Con⁃struction-Latest Developments，London，2000：1-12.

［4］PYSZKO R.Strength assessment of a version of joint of sandwich panels［J］.Polish Maritime Research，2006，（s1）：17-20.

［5］NIKLAS K.Search for optimum geometry of selected steel sandwich panel joints［J］.Polish Maritime Re⁃search，2008，15（2）：26-31.

［6］KOZAK J.Selected problems on application of steel sandwich panels to marine structures［J］.Polish Mari⁃time Research，2009，16（4）：9-15.

［7］KOZAK J.Forecasting of fatigue life of laser welded joints［J］.Zagadnienia EksploatacjiMaszyn，2007，149（1）：85-94.

［8］刘涛，杨凤鹏，李贵敏，等.精通ANSYS［M］.北京：清华大学出版社，2002.

［9］张炯，袁带英.子模型方法在风力机法兰连接有限元分析中的应用［J］.现代制造工程，2010（7）：5-9.

ZHANG J，YUAN D Y.The application of sub-model in finite element analysis of wind turbine flange connec⁃tion［J］.Modern Manufacturing Engineering，2010（7）：5-9.

［10］刘慧芳，李书，柯志强.基于子模型方法的连接机构接触模型及其应用［J］.飞机设计，2009，29（1）：25-29.

LIU H F，LI S，KE Z Q.The contact model of connect⁃ing mechanism and its application basing on the sub-model method［J］.Aircraft Design，2009，29（1）：25-29.

Strength Analysis on Model I-Core Steel Sandwich Panel Joints

WANG Hu CHENG Yuan-sheng LIU Jun

School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China

The laser welded steel sandwich structures have been used in ship structures.The strength of joint between sandwich panels is one of the key concerns for designers.The models for analyzing the strength properties of two typical joints of I-core steel sandwich panel were proposed by ANSYS，in which shell-solid assembly together with submodel method was employed.Compared with the results of the model wholly meshed with brick element，the computational accuracy of stresses near the welded region between the panel and joint member under in-plane load and out-of-plane load by using four kinds of shell-solid assemblies and submodel method was testified.They were multipoint constraints，degree of freedom cou⁃pling，defining constraints equations and creating shell element on the shell-solid interface.It is shown that the balance between good accuracy and convenience in operation can be reached by selecting suitable shell-solid assemblies，such as multipoint constraint with shell-solid constraint option and creating shell element on the shell-solid interface，together with sub model method and right mesh of main model.The computational scale is greatly reduced by the proposed models.

steel sandwich panel；joint；sub model；shell-brick assembly；ship

U661.43

A

1673－3185（2012）03－51－06

10.3969/j.issn.1673－3185.2012.03.010

2011－11－28

国家部委基金资助项目（×××0402010102）

王 虎（1986－），男，硕士研究生。研究方向：结构分析与优化。E⁃mail：san-hu@qq.com

程远胜（1962－），男，教授，博士生导师。研究方向：结构分析与优化、结构振动控制、结构抗爆抗冲击。E⁃mail：yscheng@mail.hust.edu.cn

程远胜。

［责任编辑：卢圣芳］