基于熵权的模糊集对模型在港口水域通航风险评价中的应用

徐广波，轩少永，尤庆华

(上海海事大学 商船学院，上海 201306)

0 引言

经济全球化进程的不断加快和国际贸易的不断扩大，促进船舶与港口工程的繁荣和进步、海上交通流量不断增加;与此同时，各种海损事故(船舶碰撞与搁浅、沉船、火灾、爆炸等)也不断发生.［1］由于此类事故大多发生在港口水域，因此对港口水域通航风险的评价分析受到广泛重视.

港口水域的交通风险主要是由港口水域通航环境的开放性和不确定性造成的.目前，用于通航风险评价的方法很多，主要有模糊综合评价法和灰色聚类分析法［2］、物元分析法［3］、未确知测度模型分析法［4］等，这些方法可以有效解决所获信息中的不确定性问题，但是由于在表达对象间关系时仅用一个定量指标描述，难以反映对象间的关系结构和不确定性关系的动态特征.

本文采用基于熵权的模糊集对分析模型，从同、异、反3个方面刻画事物的属性，用联系度衡量事物的各种属性特征，引入信息熵确定权重，从而对港口通航风险作出合理、客观的评价.

1 港口水域通航风险成因分类

影响港口水域通航风险的因素很多，本文采用文献［4］所确立的指标体系作为港口水域通航风险指标体系，见图1.

图1 港口水域通航风险指标体系

依据台州港实际情况，采用风和流影响程度、航道长度、航道最浅水深、航道宽度、助航设施状况、航道交叉点数、航道弯曲状况、与碍航物的距离、与泊位的距离以及VTS 服务等10 项指标，对台州港港口水域航行环境进行评价.

2 基于熵权的模糊集对模型

集对分析(SPA)是基于对立统一观点和事物普遍联系的观点建立的.SPA 通过联系度表达式展示关系的整体和局部结构，表达多种不确定性关系.基于SPA 的优良特性，其在哲学、数学、信息管理、人工智能、水利、资源环境等领域得到广泛应用.

2.1 SPA 基本原理

SPA 理论是我国学者赵克勤［5］于1989 年提出的处理不确定性问题的系统理论方法，其核心思想是把确定和不确定视为一个系统，将确定性分为“同一”和“对立”两个方面，将不确定性称为“差异”，从同、异、反3 方面分析事物及系统.集对是指有一定联系的两个集合构成的对子.在具体的问题背景下，分析由集合A和集合B 所组成集对的特性，在得到的N个特性中，有S个为集对中两个集合所共有，在另外P个特性上两个集合相对立，在其余F个特性上关系不确定，则两个集合的联系度

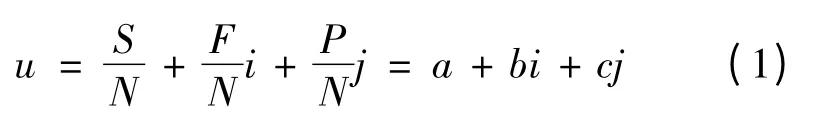
式中:u为联系度;S/N为集合A 与集合B 的同一度，简记为a;F/N为差异度，简记为b;P/N为对立度，简记为c;i为差异度因数，在［-1，1］区间视情况取值，i 也可仅起标记作用;j为对立度因数，其值为-1，j 同样也可仅起标记作用.根据定义，a，b和c应满足归一化条件［6］:

进一步将式(1)中的 bi 拓展为 bi=b1i1+b2i2+…+bk-2ik-2，可以得到多元(k 元)联系度:

式中:b1，b2，…，bk-2为差异度分量，即差异度有不同的级别和层次.该理论可以描述随机、模糊、灰色等常见的不确定性问题.

2.2 模糊集对模型

假设评价指标集A={a1，a2，…，am}和评价标准集B={b1，b2，…，bn}构成评价矩阵H=(A，B)=(hlk)，其中1≤l≤m，1≤k≤n，评价矩阵为

式(3)中取k=5，建立5 元联系度u=a +b1i1+b2i2+b3i3+ cj，根据港口环境评价指标的特性，将其分为越小越优型和越大越优型.对越小越优型指标，其联系度［7］

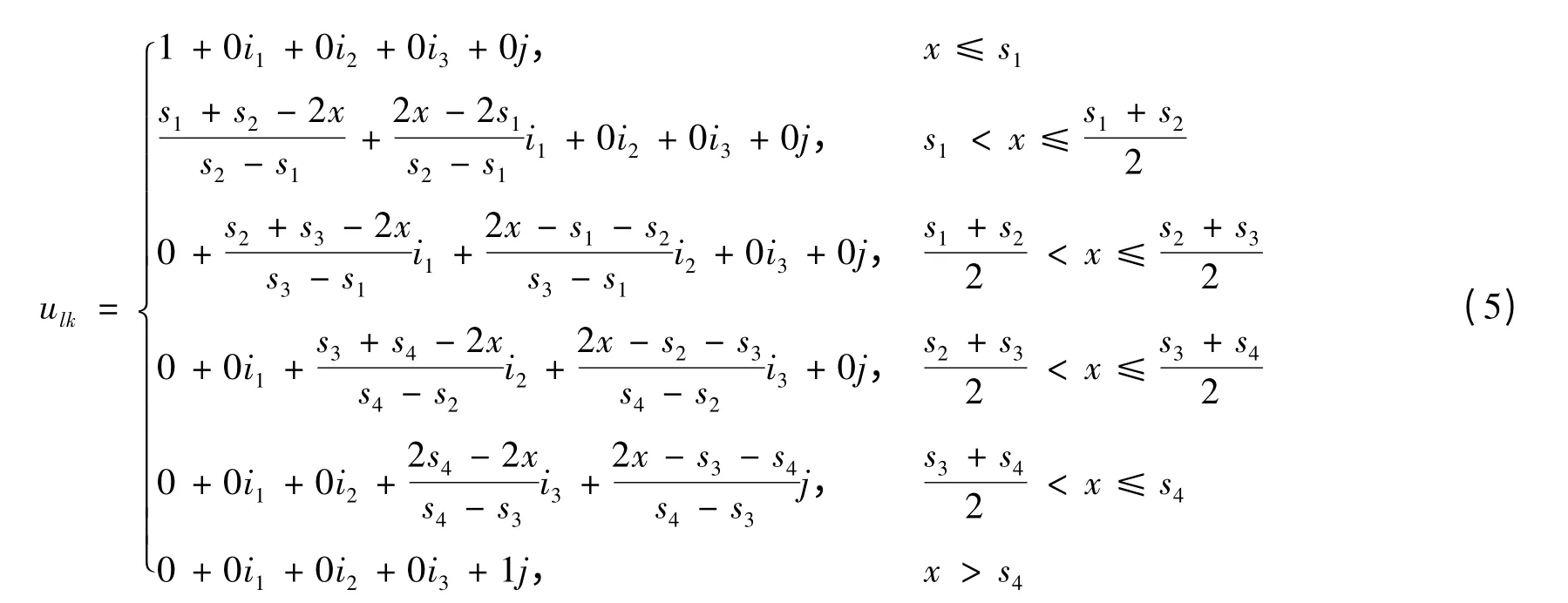
对越大越优型指标，其联系度

式中:s1，s2，s3和s4分别为评价指标的门限值;k为第k 项评价指标;l为第l个待评价测点;x为测点l的第k 项评价指标的实测值.

2.3 熵权法确定指标权重因数

在信息论中，熵是系统无序度的度量.熵权反映各指标向决策者提供的有用信息量，通过信息熵构建指标权重，可以尽量消除各指标权重计算的人为干扰，使评价结果更符合实际，其计算步骤［8］如下:

(1)假定有m个被评价对象，每个被评价对象有n个评价指标，构建判断矩阵

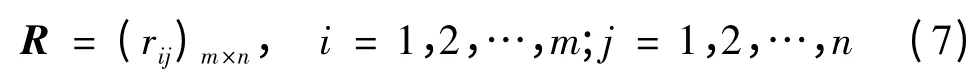
(2)将判断矩阵R 归一化，得到归一化矩阵B，B 的元素为

式中:rmax和rmin分别为同一评价指标下不同事物的最大值和最小值.

(3)根据传统的熵概念可定义各评价指标的熵

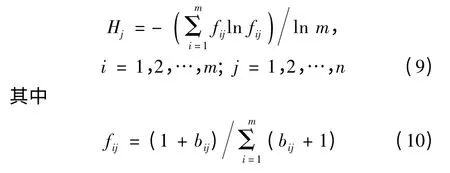
(4)计算评价指标的熵权

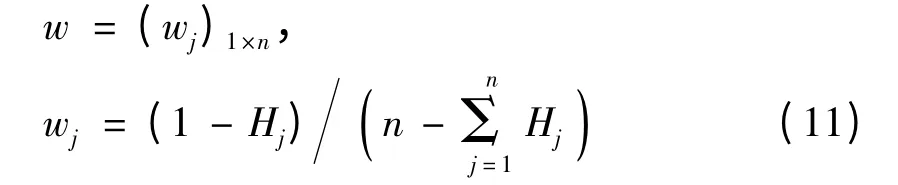
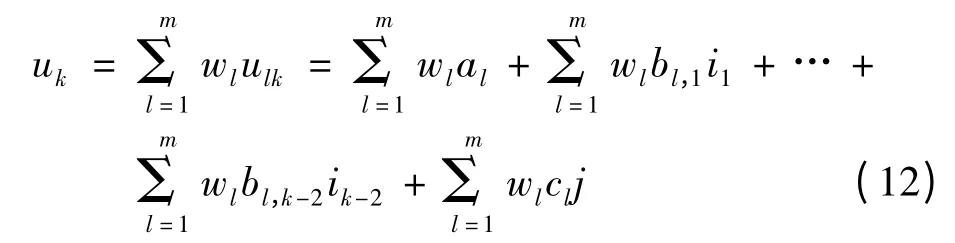
判断危险度等级标准，最终可得出评价结果.

3 实例应用

根据所建立的基于熵权的模糊集对模型，采用文献［4］中的台州港水域的通航环境指标分类标准(见表1)和通航环境指标(见表2)进行分析.

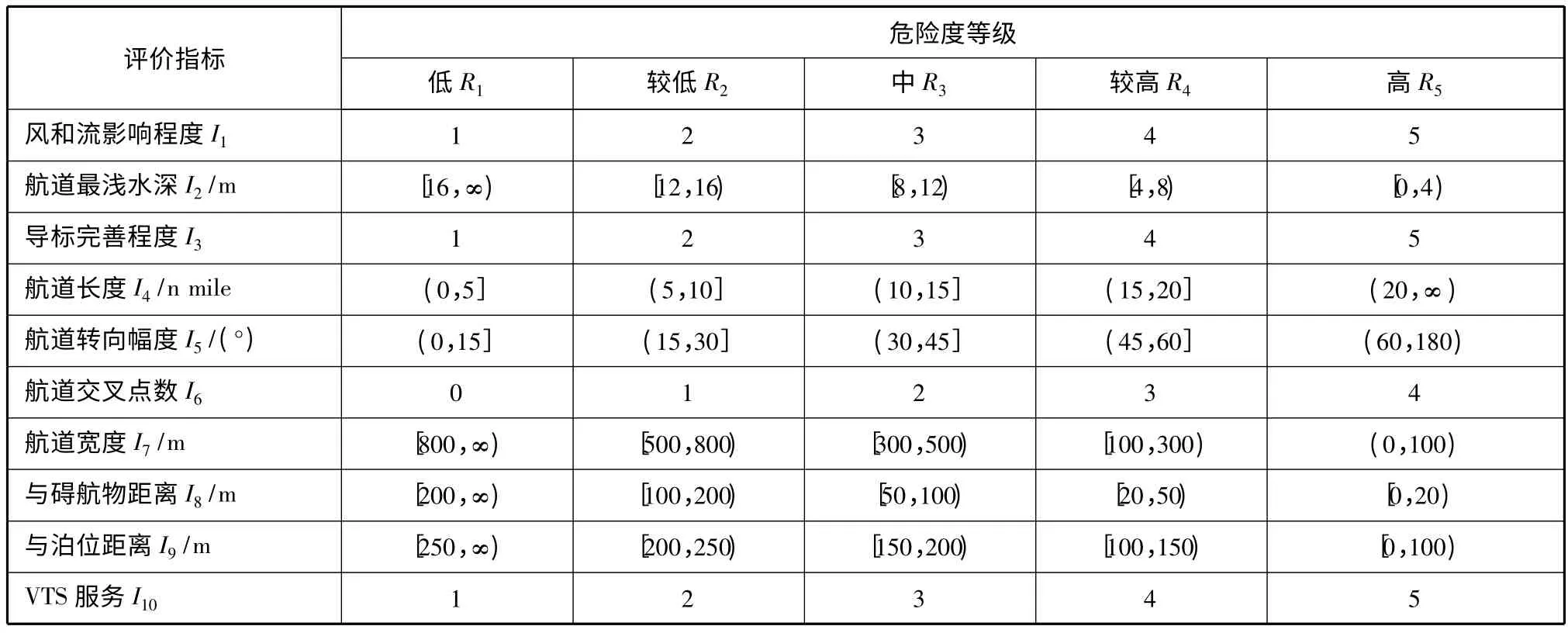
表1 通航环境指标分类标准

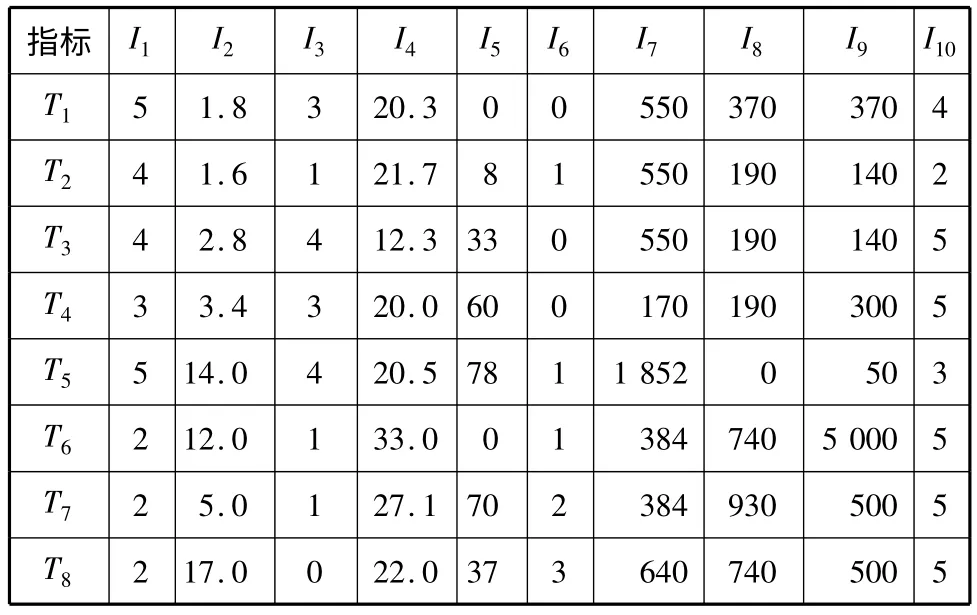
表2 台州港通航环境指标

表2中:T1为1 号浮到牛头颈航段;T2为牛头颈到三江口航段;T3为三江口到红光码头航段;T4为健跳港进港航道;T5为大麦屿进港航道;T6为龙门进港航道;T7为全清进港航道;T8为大陈岛进港航道.

3.1 单一航段各指标联系度的计算

根据表1和2，用公式(5)或(6)计算台州港任一航段T3各指标的联系度，结果见表3(限于篇幅，不再列出其他航段指标的计算结果).

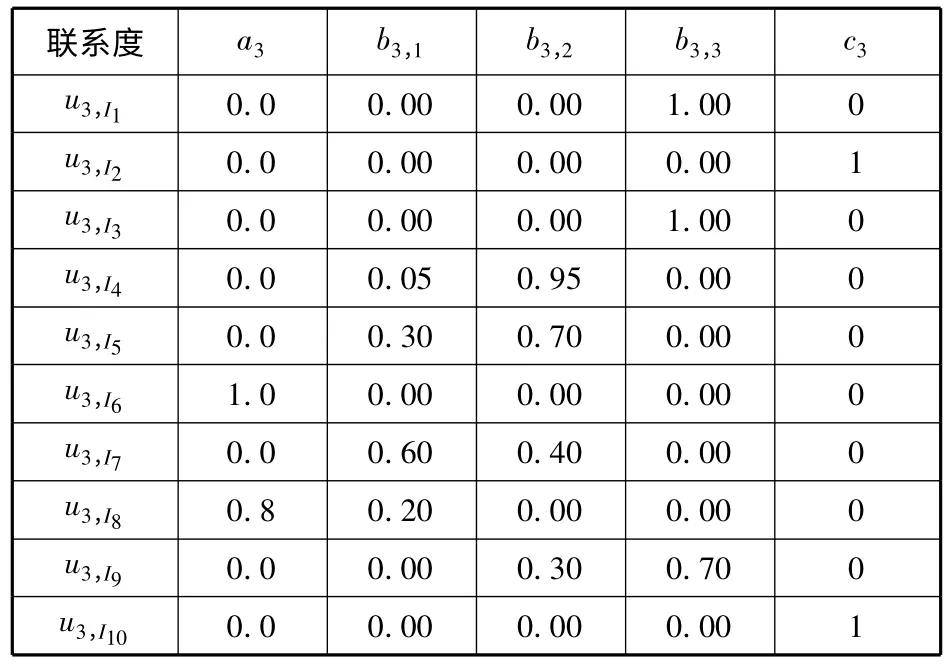
表3 T3航段各指标联系度

3.2 计算各指标权重及各航段联系度

利用式(8)～(11)计算各指标的权重

根据式(12)计算各航段联系度，见表4.

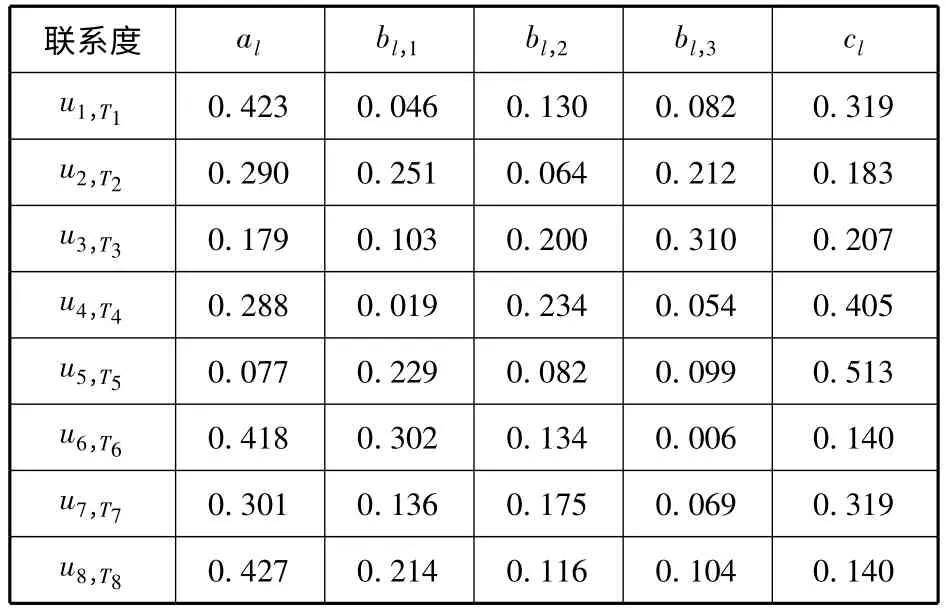
表4 台州港各航段联系度

3.3 分析评价计算结果

根据式(13)，取置信度λ=0.60，计算各航段危险度等级.对于T1航段，取k=3 时，h3=0.599 ＜0.60，考虑到其同一度a1=0.423，因此判定该航段危险度等级为中;对于T3航段，取k=3 时，h3=0.482 ＜0.60，取k=4 时，h4=0.792 ＞0.60，因此判定该航段危险度等级为较高.用相同的方法判定其他航段的危险度，各航段评价结果见表5.

根据表5 所列结果，建立基于熵权的模糊集对模型计算结果P1与文献［4］中基于熵权的未确知测度计算结果P2的集对H1=(p1，p2)，计算其联系度up1-p2，同时建立基于熵权的模糊集对模型计算结果P1与文献［9］中基于组合赋权的未确知测度计算结果P3的集对H2=(p1，p3)，计算其联系度up1-p3.将P1和P2的排序结果按符号进行对比，统计符号相同的个数S，差异一(差1 级)的个数F1，差异二(差2 级)的个数F2，差异三(差3 级)的个数F3和相反(差4 级)的个数P，由公式(1)和(3)得up1-p2=0.625 +0.125i1+0.125i2+0.125i3+0j，其中同一度a=0.625(强同一性)，对立度c=0，说明两种方法的评价结果基本一致.同理，up1-p3=0.625 +0.25i1+0.125i2+0i3+0j，其中同一度a=0.625(强同一性)，对立度c=0，说明这两种方法的评价结果也基本一致.

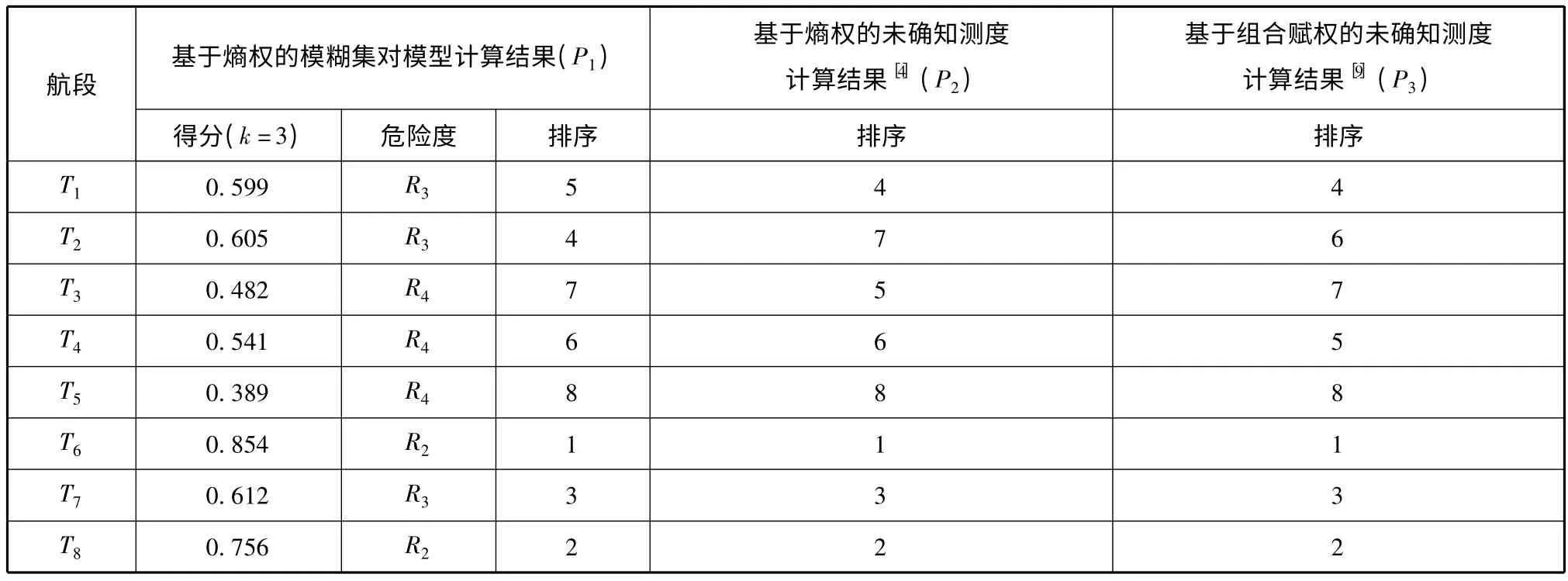
表5 台州港各航段交通风险的评价结果

4 结束语

应用集对分析理论建立港口水域通航环境影响因素的评价模型，基于SPA 原理，将通航环境与其安全标准构成一个集对，运用信息熵确定指标权重，分析各航段指标的同一、对立和差异，根据计算的联系度以及置信度判别准则，对台州港口水域的通航环境进行危险度评价.计算表明，本文的评价结果与文献［4］和［9］的评价结果具有较好的一致性，所用方法有利于针对原始数据进行数据挖掘和数值分析，与未确知度数学方法相比，可以较好地剔除主观信息，获得非人为因素控制下的评价结论.

［1］张圣坤，白勇，唐文勇.船舶与海洋工程风险评估［M］.北京:国防工业出版社，2003:1-20.

［2］周丽丽，胡甚平.船舶引航风险成因灰色综合评价模型［J］.上海海事大学学报，2008，29(3):21-25.

［3］张文青，胡甚平，刘琨，等.基于熵权的海上交通风险成因物元评价模型［J］.上海海事大学学报，2010，31(2):18-27.

［4］李伟，胡甚平，尤庆华，等.港口水域通航风险评价的未确知测度模型［J］.上海海事大学报，2009，30(3):13-21.

［5］赵克勤.集对分析及其初步应用［M］.杭州:浙江科学技术出版社，2000.

［6］ZHOU Jianfeng.SPA-fuzzy method based real-time risk assessment for major hazard installations storing flammable gas［J］.Safety Sci，2010，48(6):819-822.

［7］王文圣，李跃清，金菊良，等.水文水资源集对分析［M］.北京:科学出版社，2010.

［8］孟宪萌，胡和平.基于熵权的集对分析模型在水质综合评价中的应用［J］.水力学报，2009，40(3):257-262.

［9］席永涛，沈淳，方泉根，等.基于未确知测度的引航水域风险预评估［J］.船海工程，2009，38(1):56-58.