航道关键段动态通航饱和度模型及其应用
2012-07-06杨小军肖英杰冯宏祥
杨小军,肖英杰,冯宏祥
(上海海事大学a.商船学院;b.航运仿真技术教育部工程研究中心,上海 201306)
0 引言
随着航运事业的不断发展,我国海上运输日益繁忙,船舶交通更加拥挤、通航密度持续增大、通航环境日趋复杂,越来越多的航道直接面临趋于饱和的挑战.为了保持港口可持续稳定的发展,确保船舶在航道安全畅通地航行,有必要对航道通过能力和航道饱和度现状进行分析及评估,作出科学论证,以便配套航道能够适应各港口的发展需求,对航道进行有计划的合理开发和综合规划.
国内学者通过不同的方法研究受限航道的通过能力,其中LIU 等[1]运用排队论对受限航道通过能力进行计算;邵俊岗等[2]运用排队论对港口通过能力进行综合评估;李子强[3]通过交通流的分析对航道通过能力进行研究;代君等[4]运用船舶领域模型对港口受限航道通过能力的计算方法进行探讨.
国外文献对航道通过能力的研究主要集中在早期的苏伊士运河、巴拿马运河等一些狭水道以及日本的部分海河航道,研究方法大都基于模型预测和仿真模拟进行分析,缺乏有力的数据支撑.且原有的静态模型和分析方法不能反映真实的交通情况,适用性较差,得出的结论也常常与实际情况有所偏差.[5-8]
1 内河航道通过能力
内河航道通过能力(或称航道容量)一般是指在一定的船舶技术性能和一定的运行组织条件下,一定航道区段单位时间(年、月、日或航期)内可能通过的最大货物吨数或船舶吨数.其中,前者又称货物通过能力,以万t/a为计算单位,后者又称船舶通过能力,以万艘/a为计算单位.
对于内河航道通过能力的确定,水运工程学者先后提出多种计算方法[9],如西德公式、长江公式、苏南运河公式、闵朝斌公式、川江航道公式、利用乘潮水位航道的通过能力计算公式、王宏达公式等.[7]其中,长江公式为

式中:WB为双向双行货流通过能力;C为上、下行载货不平衡因数;W为通航船队总载重吨;F1为年通航期因数;F2为非标准船队影响总载重吨因数;F3为各港发船不均衡,使船队非等距离通过桥孔的影响因数;F4为考虑非载重船舶通过控制段影响因数;t为船队通过桥孔或其他控制河段时间.
航道饱和度S是反映航道服务水平的重要指标之一.根据交通工程学原理可理解为:航道饱和度是在保证航道安全运作的前提下,航道上实际通过的船舶流量Q 与航道通过能力C 之比值[10-11]:

式中:船舶流量Q是指在单位时间内通过某一航道的船舶数量.可以通过对船舶交通进行观测和调查获得船舶流量的数据.
2 航道动态通过能力模型
对航道通过能力的定义有两种:第一种是静态通过能力,主要是指航道在自然条件、船舶交通状况均为理想状态下单位时间内的最大交通量;第二种是动态通过能力,主要是指在现实航道条件和交通状况下单位时间内的最大交通量,其随现实航道条件和交通状况的变化而动态变化.由于航道中通航船舶的尺度、性能和速度不同,航道中的水深、地形、潮流必然会影响船舶交通;同时,追越、交会等交通行为也对航道通过能力产生影响.因此,动态航道通过能力是指在具体约束条件下,航道具有的通过能力,其数值通常小于静态航道通过能力.
与静态通过能力相比,影响动态通过能力的因素较多,现选取3个主要的影响因素(船舶流密度、船舶交会和追越行为、由潮汐变化等引起的航道水深变化)对静态航道通过能力进行折减,得到动态航道通过能力模型[3]:

式中:Cd为动态航道通过能力,艘/h;W为水道宽度,km;ρmax为单位水道宽度上船舶密度最大理论值,艘/km2,可根据船舶领域形状和大小以及排列因素确定;V为船舶平均速度,km/h;a1为船舶流密度增大时,船舶航行阻力增加引起的通过能力折减因数;a2为船舶交会、追越时引起的航速损失因数;a3为由潮汐变化引起的航道水深变化影响因数.
a1是考虑到在双向航道中,船舶对向航行发生会遇或同向航行发生追越时,为避免船吸现象、发生碰撞事故以及减少船行波带来的影响而减速航行.a2是考虑航道内船舶密度较大时,船舶航行的自由度受到限制,不能以较高航速航行,导致通过能力下降.a3是考虑潮汐变化时航道的水深也随之变化,导致一些大吨位船舶受吃水限制难以在低水位时通航,使得此时的通过能力下降.
3 航道动态饱和度模型
由于船舶流量随时间变化,可以采用日平均船舶流量、月平均船舶流量或年平均船舶流量表示.由于航道中行驶的船舶大小规模不同,如船舶流量的单位只用单位时间内通过的船舶数量表示,而不考虑通过船舶的尺度和吨位,就不能确切地反映出航道内船舶交通流的拥挤程度和危险程度.因此,可以采用L 换算因数或L2换算因数(L为船长)进行标准船舶流量换算.
当通过能力取动态航道通过能力Cd时,航道饱和度即是动态航道饱和度

动态饱和度的取值可以大于1,当Q <Cd时,Sd未达到饱和状态;当Q=Cd时,Sd达到饱和状态;当Q >Cd时,Sd达到过饱和状态.出现过饱和状态的原因是静态通过能力与动态通过能力之间存在差值,这部分差值是航道的富余通过能力,当船舶流量占用富余通过能力时会出现航道非常拥挤、驾驶员感觉不安全的现象,此时容易发生水上交通事故.

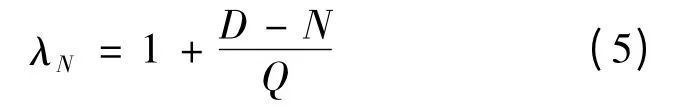
4 研究应用
4.1 流量观测数据
于2010 年10 月07 日12:00—2010 年10 月10日12:00 对长江江苏段航道比较典型的断面即苏通大桥断面进行72 h AIS 流量观测,以获取最新的具有代表性的流量数据,观测断面见图1.

图1 苏通大桥AIS 流量观测断面轨迹分布
4.1.1 标准船的确定与船型的船长转换
根据流量观测资料,船长在50~100 m 及100~180 m 区间内的船舶数量占船舶总流量的79.2%,长度<50 m 的船舶数量占船舶总流量的16.2%;长度>180 m 的船舶数量占船舶总流量的4.6%.因此,不妨将100 m 作为标准船船长L*,其他类型船舶通过L/ L*予以折算.此时,可认为标准船领域的长轴为600 m,短轴为160 m.
4.1.2 苏通大桥主通航孔航道宽度
设置苏通大桥大船主通航孔航道宽度为500 m双向通航,中间有100 m 分隔带,因此航道宽度取400 m.
4.1.3 苏通大桥断面船舶速度
通过流量观测统计分析,长江江苏段过境船舶的平均航速都控制在9 kn 左右,为方便计算换算成16.7 km/h.
4.2 动态通过能力计算
船舶领域是由日本学者藤井弥平提出的,该模型是以船舶为中心、长半轴沿船舶首尾线方向、短半轴沿船舶正横方向的一个椭圆.一般认为,在航道或港内航行时,船舶领域尺寸为6 L/1.6 L[4,12].
如果船舶流密度增大时,a1取0.9,a2和a3取0.8,则苏通大桥断面的动态通过能力

4.3 动态饱和度、船舶夜航率及不均匀因数计算分析
根据苏通大桥断面船舶流量观测,该处的平均船舶流量折算为16.9 艘/h.
由式(2)和(3)可知,该断面航道的动态饱和度

根据苏通大桥断面船舶流量观测、船舶流量折算、护航和封航以及特殊天气时的因素,对航道饱和度进行综合评价,分析得出苏通大桥断面的平均夜航率为37.61%,特殊情况下夜航率为23.14%.由此可见,鉴于目前的船舶夜航率,昼夜船舶流量的不均匀因数

特殊情况下昼夜船舶流量的不均匀因数
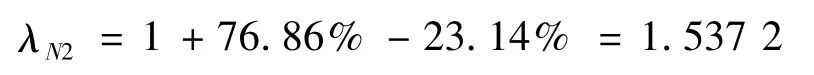
该断面的平均船舶流量昼夜不均匀航道动态饱和度

该断面的特殊船舶流量昼夜不均匀航道动态饱和度

该断面的船舶流量封航1 h 通航航道动态饱和度

该断面的船舶流量封航2 h 通航航道动态饱和度

根据特殊船舶护航和封航流量昼夜不均匀饱和度分析,动态航道饱和度在封航2 h 及以上情况下达到饱和.
由于恶劣天气、能见度不良以及其他天气情况下船舶通航受限时,航道动态饱和度的计算与封航时基本一致,主要取决于受限程度及受限时间.
根据长江江苏段航道关键段的航道通过能力和饱和度指标分析,特别是考虑昼夜不均匀因数、护航、封航和特殊天气状况等因素时,长江江苏段航道关键段存在通过能力受限、航道饱和的现象.
5 结 论
主要通过对航道通过能力和饱和度的研究,建立改进的航道关键段船舶动态通航能力和动态饱和度计算模型.最后,结合长江江苏段航道关键段的船舶流量,对长江江苏段航道关键段通过能力和饱和度进行应用分析,证明该模型可以得到更加接近实际情况的分析结果.
[1]LIU Jingxian,HAN Xiaobao,YI Xiangping.Calculation of restricted channel transit capacity based on the queuing theory[C]// Proc Asia Navigation Conf 2009,Shizuoka,Japan:Japan Institute of Navigation,2009:81-86.
[2]邵俊岗,许小兵,王煜,等.洋山港区运营阶段的港口通过能力[J].上海海事大学学报,2008,29(4):25-28.
[3]李子强.基于交通流分析的航道通过能力研究[J].武汉航海(武汉航海职业技术学院学报),2009,4(2):9-13.
[4]代君,王当利,刘克中.基于船舶领域模型的港口受限航道通过能力计算方法[J].武汉理工大学学报,2009,33(4):679-682.
[5]YANG Xingyan,JI Hua,LI Wei.Study on the navigation capacity of the approach channel of Tianjin Port[J].Port Technol Int,2006(34):45-47.
[6]BLUME A L,HIGH J P.Toward a better understanding of waterway capacity[J].On Course PIANC Mag AIPCN,2005(118):27-34.
[7]EMTISSAL M H L.The maximum shipping capacity of the new physical layout of the Suez Canal[J].Egypt Comput J,1987(4):79-96.
[8]FRANKEL E G,LIM C S.Capacity algorithms for navigational channels[C]// PIANC 27th Int Navigation Congress,Osaka,Japan.1990:97-103.
[9]刘敬贤.大型海港进港主航道通过能力及交通组织模式研究[D].武汉:武汉理工大学,2009.
[10]李国帅.虾峙门航道通航能力及饱和度的研究[D].大连:大连海事大学,2008.
[11]吕立生,沈庚余.黄浦江航道的饱和度及应用[J].上海大学学报:自然科学版,1998,4(2):207-212.
[12]吴兆麟,朱军.海上交通工程[M].大连海事大学出版社,1999:117-121.
