基于UG的准双曲面齿轮的加工仿真
2012-07-06陈卫强张卫青
陈卫强,张卫青,赵 铭
(重庆理工大学重庆汽车学院,重庆 400054)
如今准双曲面齿轮被汽车、机械等行业大量采用,特别是广泛地被应用于重型车驱动桥的主减速器上。相比其他齿轮,准双曲面齿轮不仅能够传递相交轴的扭矩,而且具有强度高、传动平稳性好等优点,但同时其轮齿形状和结构也相应复杂很多,属于三维空间自由复杂曲面,因而加工原理及方法也相对复杂得多。目前,国内外广泛采用机械式及全数控铣齿机进行加工。当准双面齿轮的加工调整参数设计出来后,依然不能判断出加工后的齿轮齿形是否正确,这样在实际加工过程中就需要通过不断地试切来检验齿形和优化参数。而对于仿真加工而言,它是实际加工过程在仿真软件上的模拟,在实际加工前就能够准确地判断出准双曲面齿轮的齿形结构,对提高准双曲面齿轮的开发效率,降低加工成本具有重要的指导意义。
1 准双曲面齿轮仿真加工的运动控制方法
1.1 铣齿机的切齿加工原理
在实际加工中,普遍采用展成法加工准双曲面齿轮,其加工原理就是基于齿轮的啮合原理,将铣齿机上的摇台机构看成一个与加工齿轮相啮合的齿轮,将安装在摇台上的刀盘的切削运动看成是产形轮的一个齿。当齿坯和产形轮按确定的速比旋转时,刀盘切削齿坯,进而加工出一个齿槽。实际上,可以把齿坯的加工过程看成是一对齿轮的啮合过程,其中加工齿轮的齿面和刀盘的切削面处于完全共轭的状态。
1.2 齿坯和刀盘相对位置和运动的控制
在此次仿真模拟数控铣齿机的运动模式中,将摇台的转动转换为坐标轴上的移动,通过计算和改变加工过程中齿坯和刀盘的坐标位置来控制它们的运动。
为了清楚地描述齿轮的加工过程,建立了如图1所示的坐标系。由于采用普通滚切法加工,所以机床模型为无刀倾装置铣齿机。取Σ为与大地固连的静坐标系,位置和机床坐标系起始位置相同,机床坐标系为,原点o为摇台平面的中心点r平面在摇台平面上并垂直于摇台轴线向量为摇台的水平轴截面和摇台平面的交线的方向垂直并指向于摇台背面。在刀盘的中心位置建立一个坐标系在刀盘平面内并与摇台平面共面的方向由o指向

图1 齿坯和刀盘的相对位置关系
根据要求,在加工前把水平轮位X、床位Xbr、安装根锥角Γ以及垂直轮位Emr调整好。则Σ的原点o到齿轮轴线的轴交错点的径矢为
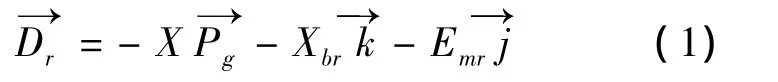
同时Σ的原点o到刀盘中心的矢量在Σ坐标系下可表示为

通过以上计算可以得出:在qt时刻,刀盘中心ok在静坐标系Σ的位置用标量表示为

同样,齿轮轴线轴交错点og在静坐标系∑的位置用标量表示为
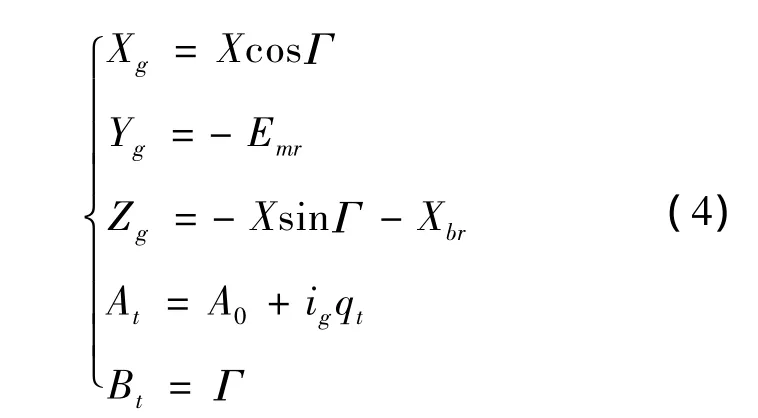
式(3)(4)中:A0为加工前齿轮转轴的初始角度;ig是产形轮与加工齿轮之间的传动比;At是t时刻齿轮转轴A的角度值;Bt是t时刻调整加工根锥角转轴B的角度值。因此,在UG中进行仿真加工时,可以通过改变静坐标系Σ下刀盘中心和轴交错点的X、Y、Z、A、B的坐标值来控制齿坯和刀盘的相对位置和相对运动。
2 准双曲面齿轮的仿真加工在UG中的实现
齿轮加工是刀盘从齿坯上切除材料的过程。只有当齿坯和刀盘的切削面之间存在瞬时重叠区域时,刀盘才能去除材料,所去除的材料部分就是重叠区域部分,所以齿轮的加工过程就是去除瞬时重叠区域的过程。本次加工仿真正是根据该原理,在UG中建立齿坯和刀具的三维实体,控制它们的相对运动,通过布尔运算来去除瞬时重叠区域,进而模拟出实际的加工过程[6]。
2.1 UG中齿坯和刀盘模型的建立
齿坯属于旋转体零件。对于旋转体的构建,主要是要确定其二维截面图。齿坯的二维截面参数可以由齿宽、面锥角、冠顶距、大端直径等参数确定。画出的齿坯二维截面如图2所示。在UG中选中截面执行旋转命令,让其绕自身轴线旋转1圈就完成了齿坯三维模型的建立。
加工齿轮的铣刀盘也属于旋转体零件,且刀盘上安装了1圈不连续的内外刀齿。在加工过程中,刀盘上刀齿连续地旋转运动形成了内外2层圆锥切削面,因此,在加工仿真过程中,可以用圆锥面代替刀盘的切削面。其二维截面图可以根据刀盘名义半径、内外刀齿齿形角和刀尖错距等参数确定,所画出的刀盘截面如图3所示。在UG中选中截面执行旋转命令,让其绕自身轴线旋转1圈就完成了刀盘三维模型的建立[3]。
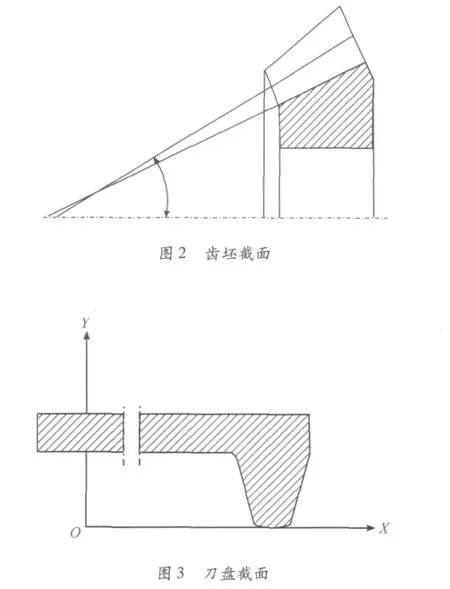
2.2 准双曲面齿轮加工仿真过程
此次仿真采用普通滚切法加工小轮,采用成形法加工大轮。当加工大轮时,只需计算加工参数调整后的刀盘和齿坯的起始位置即可,然后将刀盘移动到切入位置,此时工件和刀盘出现重叠区域,通过布尔运算将其去除,根据加工齿轮的齿数对工件进行旋转分齿。重复之前操作直至加工出所有的轮齿。
当采用滚切法加工小轮时,每个时刻刀盘和工件的位置都需发生变化才能加工出小轮的齿槽。已知qt和机床调整参数,可以确定任意时刻刀盘中心和齿轮轴交错点的坐标位置。假设切齿过程中刀盘中心到静坐标系原点o的连线与→—i之间的初始夹角为qs,终止夹角为qe,同时设定夹角的步进值为dq,则任意时刻的夹角qt=qs+n×dq,改变n的值可以得到一系列的刀具和工件的坐标位置。每步进一个位置,刀具和齿坯的坐标位置发生改变,并且会产生出新的瞬时重叠区域,通过布尔运算将其去除,直到将刀盘中心移动到终止夹角qe位置时,刀盘和工件开始分离。之后把刀盘中心移动到初始位置,并根据加工齿轮的齿数对工件进行旋转分齿。重复以上操作,直至加工出所有的轮齿。
3 准双曲面齿轮加工仿真实例
加工仿真所选用的准双曲面齿轮副的基本参数见表1,机床调整参数及刀盘参数见表2。

表1 准双曲面齿轮的基本参数
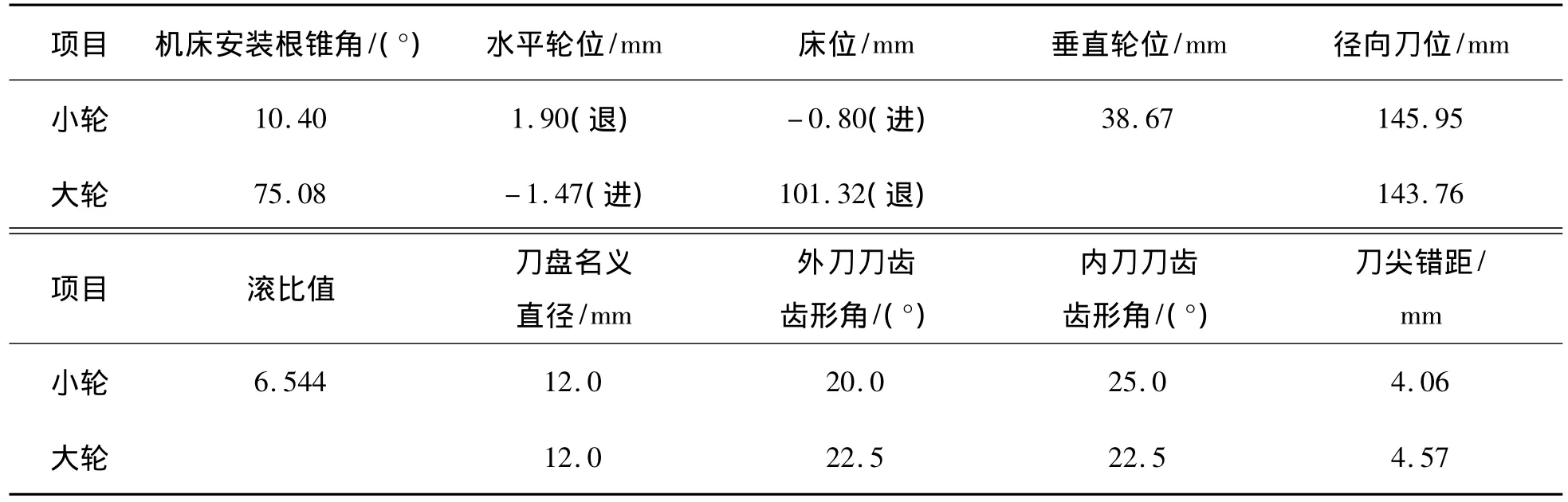
表2 机床调整参数及刀盘参数
根据表1~2给出的齿坯参数和机床调整参数,通过控制齿坯和刀盘的相对运动仿真加工出了一对准双曲面齿轮。大轮切齿加工过程和仿真加工后的大轮模型分别如图4及图5所示;小轮仿真加工过程和加工后的小轮模型分别如图6及图7所示。
结果表明:所加工的准双曲面齿轮轮齿收缩正常,齿底无根切,是一对正确啮合的准双曲面齿轮副。

图4 大轮切齿加工过程

4 结束语
依据齿轮加工原理研究了切齿运动控制方法,描述了在UG软件中刀具和齿坯的建立及准双曲面齿轮的仿真加工过程,最后对一对准双曲面齿轮进行了仿真加工。结果表明:本文的切齿运动控制方法正确,仿真加工出的准双曲面齿轮效果良好。
[1]张卫青,张明德,郭晓东,等.全数控锥齿轮铣齿机运动控制方法及切齿实验研究[J].中国机械工程,2009(22):2733-05.
[2]郑昌启.弧齿锥齿轮和准双曲面齿轮[M].北京:机械工业出版社,1988.
[3]曹丽建,邓效忠,徐爱军.准双曲面齿轮的虚拟加工模型[J].河南科技大学学报,2009(6):16.
[4]Gleason Seminar.Spiral Bevel and Hypoid Gear Technology Update[M].Beijing:[s.n.],2007.
[5]Hermann J Stadtfeld.Handbook of Bevel and Hypoid Gears[M].New York:Rocbester Institute of Technology,1993.
[6]曾韬.螺旋锥齿轮设计与加工[M].哈尔滨:哈尔滨工业大学出版社,1989:90-111.
[7]卢春光,常炯.准双曲面齿轮的设计和制造[Z].南昌:南昌齿轮研究所,1978:144-159.
[8]Kawasaki Kazumass.A Method for Cutting Hypoid Gears[J].JSME International Journal,1997,40(4):768-775.
[9]徐彦伟,张连哄,刘德全,等.弧齿锥齿轮成形三维虚拟仿真研究[J].机械与电子,2004(1):22-36.
[10]王利环,魏冰阳.准双曲面齿轮节锥参数设计的新方法[J].河南科技大学学报:自然科学版,2008,29(2):25-27.
[11]熊越东,王太勇,张 威.螺旋锥齿轮数控加工三维仿真研究[J].制造业自动化,2005,27(6):21-23.
[12]吴序堂.格里森制准双曲面齿轮刀倾全展成切齿法的研究[J].机械工程学报,1985,21(2):54-69.
[13]周凯红,李淑.螺旋锥齿轮技术的历史、现状和展望[J].桂林航天工业高等专科学校学报,2008(3):4-8.
