几乎有限表现模
2012-07-05黄飞丹
黄飞丹
(毕节学院数学与计算机科学学院,贵州 毕节 551700)
几乎有限表现模
黄飞丹
(毕节学院数学与计算机科学学院,贵州 毕节 551700)
利用几乎有限表现模来刻划凝聚环和半遗传环.通过讨论几乎有限表现模和广义有限表现模之间的关系,得出了几个关于几乎有限表现模和凝聚环、半遗传环的等价条件,改进了已有的结论,把刻划凝聚环的模缩小到几乎有限表现模.
几乎有限表现模;广义有限表现模;凝聚环;半遗传环
1 引言
自文献[1]对交换环定义了有限表现维数以来,有限表现性已得到了广泛和深入的讨论.文献[2]给出了一般环上有限表现维数的定义,并深入讨论了有限表现维数的一些重要性质,并运用有限表现维数刻划了凝聚环.
几乎有限表现模是一种较特殊的模,且是非有限生成模,因一些常见的环(如凝聚环、半遗传环)很少用非有限生成模来刻划,故对非有限生成模,特别是对几乎有限表现模的研究比较少.文献[3]给出了几乎有限表现模的定义,并给出了几乎有限表现模的一些性质,文献[4]给出了广义有限表现模的概念,并用广义有限表现模的有限表现维数刻划了凝聚环.本文给出几乎有限表现模的一些刻划,讨论了几乎有限表现模和广义有限表现模的关系,并用几乎有限表现模来刻划凝聚环和半遗传环.对凝聚环的刻划(定理3.2)改进了文献[3-4]中的结论,其中对文献[4]中的结论,把刻划凝聚环的模缩小到几乎有限表现模.
本文所涉及的环均指有单位元的结合环,模均指左酉模.
文中涉及的一些记号:
FGRM—左有限生成模范畴;FPRM—左有限表现模范畴;
GFPRM—左广义有限表现模范畴;
fpd(M)—模M的(左)有限表现维数;
fgd(M)—模M的(左)有限生成维数.
f.g.模—有限生成模;f.p.模—有限表现模.
文中的“非f.g.自由模”指的是自由的且不是有限生成的模.
文中涉及的概念及记号可见参考文献[2-6].
2 几乎有限表现模的性质
定义2.1[3]设R是环,M是R-模,若M=M′⊕M′′,其中M′是f.p.的,M′′是非f.g.自由模,则称M是几乎有限表现的,记作a.f.p..
由定义可知,f.g.模不是a.f.p.模.


3 几乎有限表现模与广义有限表现模
定义3.1[4]设R是一个环,M是左R-模,若存在投射模P及f.g.模A,使得M~=P/A,即有正合列:
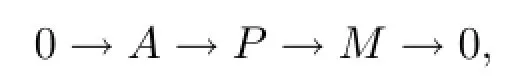
则称M为(左)广义有限表现模,也记为M∈GFPRM.此时称上面的正合列为M的广义有限表现分解.特别当P是f.g.投射模时,M就是通常的f.p.模.当A=0时,M就是投射模,从而有FPRM⊂GFPRM,ProjRM⊂GFPRM.
定义3.2[7]设R是一个环,M为左R-模,M的(左)有限生成维数记为fgdR(M),或简记为fgd(M),定义如下:
fgdR(M)=Inf{n|如果存在这样的正合列(*)Pn→Pn-1→…→P1→P0→M→0,其中Pi为投射左R-模,Pn是f.g.的},如果对于任意自然数n,如果没有(*)这样的正合列,则定义fgdR(M)=∞.
命题3.1设R是一个环,则R上的a.f.p.模是广义有限表现模.
证明设模M是a.f.p.模,则由推论2.1知有正合列0-→K-→F-→M-→0,其中K是f.g.的,F是非f.g.自由模.故M是广义有限表现模.
由于f.p.模不是a.f.p.模,故广义有限表现模不一定是a.f.p.模.
命题3.2设R是环,则对R上的任意a.f.p.模M,有fgdR(M)=1.

直接从a.f.p.模和有限生成维数的定义也可得出以上结论.
命题3.3设R是局部环,M是左R-模,若fgdR(M)=1,则M是a.f.p.模.
证明设fgdR(M)=1,则有正合列P1→P0→M→0,其中P1是f.g.投射模,P0是非f.g.投射模,由R是局部环知,P1,P0是自由模,故M是a.f.p.模.
引理3.1[4]设R为环,M是左R-模,M为广义有限表现模的充分必要条件是:存在投射模P0,自由模F*,f.p.模M0,使得M⊕P0=M0⊕F*.
引理3.1可加强为:
定理3.1设R为环,M是左R-模,M为广义有限表现模的充分必要条件是:存在投射模P0,非f.g.自由模F*,f.p.模M0,使得M⊕P0=M0⊕F*.

而Kerσ=i(K)⊂F0,所以F*~=F1,由于F为非f.g.自由模,F0为f.g.自由模,故F*~=F1为非f.g.自由模.
⇐:与引理3.1(文献[4]中)的证明类似.
在定理3.1中,M0是f.p.模,F*为非f.g.模,从而M0⊕F*为a.f.p.模,故有:
推论3.1设R为环,M是左R-模,M为广义有限表现模的充分必要条件是:存在投射模P0,使得M⊕P0为a.f.p.模.
由定理3.1的证明过程可得:
推论3.2设R为一个环且R的每个投射模均为自由模,M是非f.g.模,则M为广义有限表现模的充分必要条件是:存在非f.g.自由模F,f.p.模M0,使得M=M0⊕F.
由推论3.2直接得:
推论3.3设R为一个环且R的每个投射模均为自由模,M是非f.g.模,则M为广义有限表现模的充分必要条件是M为a.f.p.模.
引理3.2[4]设R是一个环,则下列条件等价:
(1)R为(左)凝聚环;
(2)∀M∈GFPRM,有fpdR(M)≤1;
(3)∀M∈GFPRM,若M/∈FGRM,则fpdR(M)=1;
(4)设M∈GFPRM,M1为M的任一f.g.子模,则M1是f.p.的.
引理3.3[2]设R是环,P是投射左R-模,M是左R-模,且fpdR(M)≥1,则
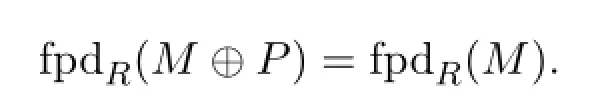
定理3.2设R是一个环,则下列条件等价:
(1)R为(左)凝聚环;
(2)∀M∈GFPRM,若M/∈FGRM,则fpdR(M)=1;
(3)对任意a.f.p.模M,有fpdR(M)=1;
(4)对任意a.f.p.模M,有fpdR(M)≤1;
(5)设M∈GFPRM,M1为M的任一f.g.子模,则M1是f.p.的;
(6)设M是a.f.p.模,M1为M的任一f.g.子模,则M1是f.p.的.
证明由引理3.2可得(1)⇔(2)⇔(5).
(2)⇒(3):设M是a.f.p.模,则M是广义有限表现模且M是非f.g.的,由假设知fpdR(M)=1.
(3)⇒(2):∀M∈GFPRM,设M/∈FGRM.由推论3.1知,存在投射模P0,使得M⊕P0为a.f.p.模,由假设知fpdR(M⊕P0)=1.由于M是非f.g.的,故M不是f.p.模,即fpdR(M)/=0,从而fpdR(M)≥1.由引理3.3知fpdR(M)=fpdR(M⊕P0)=1.
(3)⇒(4):显然.
(4)⇒(3):设M是a.f.p.模,则M是非f.g.模,故M不是f.p.模,从而fpdR(M)/=0,由假设知fpdR(M)=1.
(5)⇒(6):设M是a.f.p.模,M1为M的任一f.g.子模,由于M是广义有限表现模,故由假设知M1是有限表现的.
(6)⇒(5):设M∈GFPRM,由推论3.1知,存在投射模P0,使得M⊕P0为a.f.p.模,故M1为M⊕P0的f.g.子模,由假设知M1是f.p.的.
定理3.2的结论改进了文献[3]中的结论:若R是左凝聚环,M是a.f.p.左R-模,则fpdR(M)=1.同时也改进了文献[4]中的结论(引理3.2),把刻划凝聚环的模的范围缩小到a.f.p.模.
定理3.3设R是一个环,则下列条件等价
(1)R为左半遗传环,且任意f.p.左R-模是投射模;
(2)任意a.f.p.左R-模是投射模;
(3)对任意a.f.p.左R-模M,M的直和项是投射模;
(4)对任意a.f.p.左R-模M,M的广义有限表现的直和项是投射模.
证明(1)⇒(2):设M是a.f.p.左R-模,则M=F⊕M′,其中F是非f.g.自由模,M′是f.p.的,由假设知M′是投射模,从而M是投射模.
(2)⇒(3):由于投射模的任意直和项是投射模,故M的直和项是投射模.
(3)⇒(4):显然.
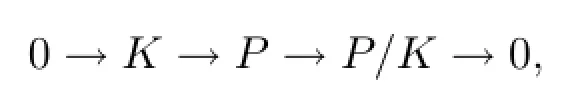
(4)⇒(1):设P是投射左R-模,K是P的f.g.子模,则有正合列:从而P/K是广义有限表现模.由推论3.1,存在投射模P0,使得(P/K)⊕P0是a.f.p.模,由假设知P/K是投射模.故正合列0→K→P→P/K→0分裂正合,从而P~=K⊕(P/K),而P是投射模,因此K是投射模.所以R为左半遗传环.对任意f.p.模M,因为M是广义有限表现模,且是某一个a.f.p.模的直和项,故由假设知M是投射模.
引理3.4[3]设R是一个环,则R是VN正则环当且仅当每个左R-模是平坦模.
推论3.4设R是VN正则环,则
(1)R为左半遗传环,且任意f.p.左R-模是投射模;
(2)任意a.f.p.左R-模是投射模;
(3)对任意a.f.p.左R-模M,M的直和项是投射模;
(4)对任意a.f.p.左R-模M,M的广义有限表现的直和项是投射模.
证明由文献[3]知R是左半遗传环.设M是f.p.左R-模,由引理3.4知,M是平坦模,而由文献[3]知f.p.平坦模是投射模,故M是投射模,从而(1)成立.再由定理3.3,(2),(3),(4)成立.
[1]Ho Kuen Ng.Finitely p rensented dimension of commutative rings and modules[J].Pacif c.J.M aths., 1984,113(2):417-431.
[2]李元林.有限表现维数和凝聚环[J].数学杂志,1991,13(2):182-188.
[3]程福长,易忠.环的同调维数[M].桂林:广西师范大学出版社,2000.
[4]李元林.广义有限表现模[J].江苏工业学院学报,1992,13(2):101-107.
[5]程福长.同调维数[M].桂林:广西师范大学出版社,1989.
[6]Anderson F W,Fuller K R.Ring and Categories of M odu les[M].New York:Sp ringer-Verlag,1974.
[7]丁南庆.模的有限生成维数[J].南京大学学报:数学半年刊,1989,6(1):107-111.
Almost finitely-presented modules
Huang Feidan
(Department of Mathematics and Computer Science, Bijie College, Bijie 551700, China)
Characterize coherent rings and semi-hereditary rings by using almost finitely-presented modules. By studying relations between almost finitely-presented modules and generalized finitely-presented modules, some equivalent conditions about almost finitely-presented modules and coherent rings and semi-hereditary are obtained. As a result, previous conclusions have been improved, and the modules using to characterize coherent rings is reduced to almost finitely-presented modules.
almost finitely-presented module, generalized finitely-presented module, coherent ring,semi-hereditary ring
O153.3
A
1008-5513(2012)02-0213-06
2011-09-10.
贵州省教育厅自然科学基金(20090068);贵州省科学技术基金(2012GZ10526);贵州省教育厅自然科学基金(黔教科2010072).
黄飞丹(1981-),硕士,讲师,研究方向:环、模及自动机理论.
2010 MSC:16D 10,16E10
