非线性一阶常微分方程解的存在惟一性
2012-07-05蒋玲芳
蒋玲芳
(西北师范大学数学与信息科学学院,甘肃 兰州 730070)
非线性一阶常微分方程解的存在惟一性
蒋玲芳
(西北师范大学数学与信息科学学院,甘肃 兰州 730070)
讨论了一类非线性一阶常微分方程边值问题解的存在惟一性.得到了当参数在一定的范围取值时解存在惟一的充分条件,并包含了一些已知结果.主要结果基于Leray-Schauder非线性抉择理论和Banach不动点定理.
一阶非线性微分方程;存在性;惟一性;Leray-Schauder非线性抉择; Banach不动点定理
1 引言及主要结果
许多物理现象都与微分方程的周期解密切相关,从而周期边值问题引起了许多作者的研究,见文献[1-6]及所附文献.特别地,2004年,文献[5]在引理1中讨论了一阶周期边值问题
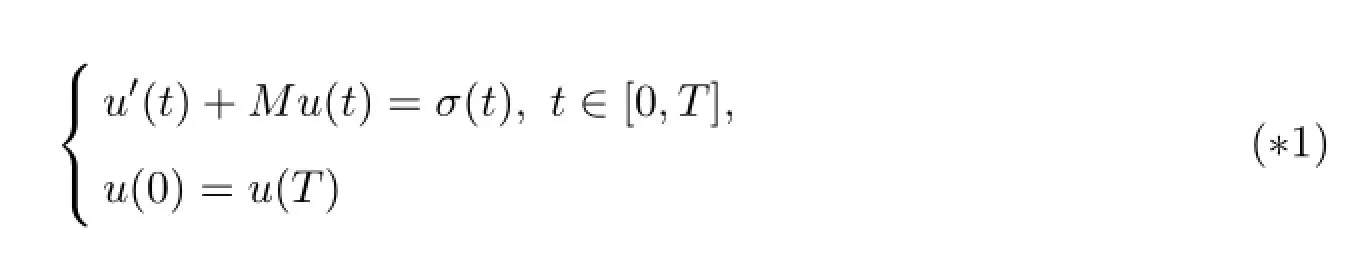
解的存在性,当M>0,则对任意的σ∈C[0,1],问题(*1)存在一个周期解.
反周期问题解的存在性等价于所研究问题倍周期变号解的存在性,因此,反周期问题解的存在性在近十几年来也得到了许多学者的广泛关注[710].特别地,2003年,文献[8]研究了一阶非线性微分方程反周期边值问题

解的存在性.并得到了下面的结论.


则(*2)式至少存在一个解.
可见,周期解与反周期解存在密切的联系,一个自然的问题,能否对周期边值问题与反周期边值问题间建立更一般的联系?本文将给出一个统一的论述.利用Leray-Schauder非线性抉择理论和Banach不动点定理考虑一阶非线性微分方程

解的存在惟一性.其中,α∈ℝ,ρ∈ℝ,λ∈ℝ为参数,且α/=eρT.
注1当α=1时,(1)式为周期边值问题;当α=-1时,(1)式为反周期边值问题.本文的结论对周期[5]和反周期问题[8]同样成立.
注2对于一阶泛函微分方程:

其中λ∈ℝ是参数,a(·)∈C([0,T],[0,+∞)),b(·),τ(·)∈C([0,T],ℝ),f,g∈C([0,T],ℝ).其中Green函数G1(t,s)为:
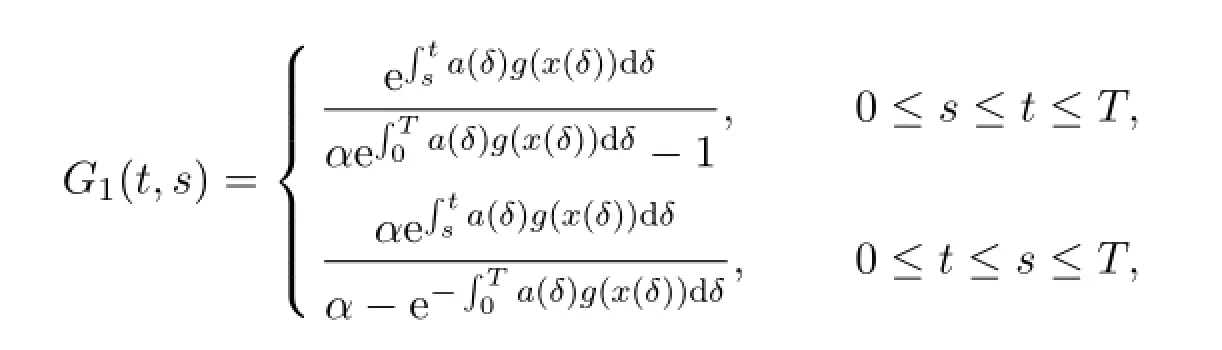
当a,g,b满足一定的条件时,本文的结论对(*)式仍然成立.
本文总假定:
(H)f:[0,T]×ℝ→ℝ为L1-Carathˊeodory函数.即满足:
(1)∀x∈ℝ,f(·,x)在[0,T]上可测;
(2)对几乎所有的t∈[0,T],f(t,·)在ℝ上连续;
(3)∀r>0,∃φr(t)∈L1[0,T].使得对几乎所有的t∈[0,T]及x∈ℝ,当‖u‖<r时,有|f(t,u(t)|≤φr(t).
Leray-Schauder非线性抉择理论:
定理A设B是Banach空间,E⊂B是有界闭凸集,若U是E中的相对开球,且θ∈U, S:fiU→E全连续.则下面结论之一成立:
(a)S在fiU中至少存在一个不动点;

2 预备知识



3 主要结果的证明

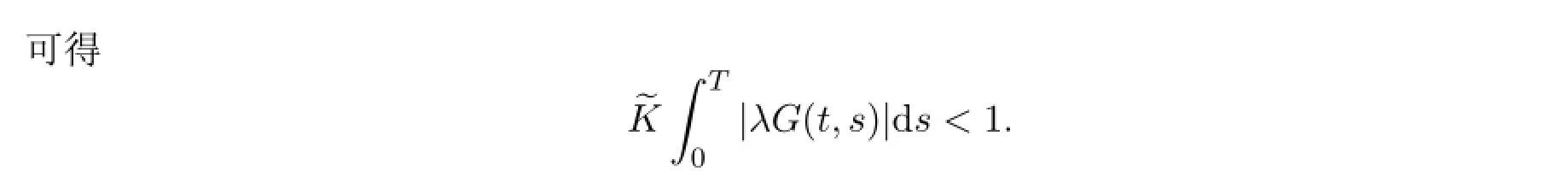
由Banach不动点定理,算子A在X中存在唯一的不动点,即(1)式在X中存在惟一解.
[1] Cheng S, Zhang G. Existence of positive periodic solutions for non-autonomous functional differential equations[J]. Electron. J. Differential Equations, 2001,59:1-8.
[2] Wan A, Jiang D. Existence of positive periodic solutions for functional differential equations[J]. Kyushu J. Math., 2002,56:193-202.
[3] Zhang G, Cheng S. Positive periodic solutions of non-autonomuos functional differential equations depending on aparameter[J]. Abstr. Appl. Anal., 2002,7:279-286.
[4] Padhi S, Shilpee Srivastava, Smita Pati. Three periodic solutions for a nonlinear first order functional differential equation[J]. Comput. Math. Appl., 2010,216:2450-2456.
[5] Peng S. Positive solutions for first order periodic boundary value problem[J]. Applied Mathmatics and Computation, 2004,158:345-351.
[6] 廖新元.非自治时滞微分方程正周期解的存在性(英文)[J].纯粹数学与应用数学,2003,19(3):268-273.
[7] Okochi H. On the existence of anti-periodic solutions to nonlinear evolution equations with associated with odd subdifferential operators[J]. J. Funct. Nonlinear Anal., 1990,91:246-258.
[8] 孙晋易,蒋玲芳,杨变霞.一类泛函微分方程反周期解的存在性[J].纯粹数学与应用数学,2011,27(2):280-284.
[9] 马如云.非线性常微分方程非局部问题[M].北京:科学出版社,2004.
[10] Franco D, Nieto J J, O'Regan D. Anti-periodic boundary value problem for nonlinear first-order differential equations[J]. Math. Inequal. Appl., 2003,6:477-485.
[11]O′Regan D.Existence Theory for Nonlinear Ordinary Diferential Equations[M].K luwer:Dordrecht,1997.
Existence and uniqueness of solutions for first-order nonlinear ordinary differential equations
Jiang Lingfang
(College of Mathematics and Information Science, Northwest Normal University, Lanzhou 730070, China)
In this paper, we show the existence and uniqueness of solutions of first-order nonlinear ordinary differential equation boundary value problem. The sufficient conditions for the existence and uniqueness of solutions are obtained when the parameter belongs to appropriate intervals, and we include some known results. The main results are based upon Leray-Schauder nonlinear alternative theorem and Banach's fixed point theorem.
first-order nonlinear differential equation, existence, uniqueness,Leray-Schauder nonlinear alternative,Banach′s fixed point theorem
O178
A
1008-5513(2012)02-0256-06
2011-06-29.
国家自然科学基金(10671158);甘肃省自然科学基金(3ZS051-A 25-016).
蒋玲芳(1989-),硕士生,研究方向:常微分方程边值问题.
2010 MSC:15A42
