构造性数学与构造集合论
2012-07-04杜文静
杜文静
(华东政法大学人文学院,上海200042)
一、引言
“循环并不可恶”[1]。Barwise和 Moss的著作《恶性循环——论非良基现象中的数学》建立了一套非良基集合理论,为各种循环现象(如,计算机科学中的流,公共知识中“知道”结构的循环,哲学中的共通悖论、说谎者悖论、指称悖论、高级游戏悖论以及罗素悖论等)提供了数学上的解释[2]。Barwise和Moss的研究是建立在包含非良基集合的经典集合论基础之上的,即公理系统ZFA(ZFC-+AFA)。Rathjen断言 Barwise和 Moss的大部分工作都可以建立在包含非良基集合的构造性全域(constructive universe)的基础上,而不是经典集合全域。也就是说,Barwise和Moss的大部分工作都可以在构造集合论(constructive set theory)的意义下进行。正如公理系统ZFC对应着康托经典数学的形式化一样,构造集合论起源于Myhill的努力,他为了找到一个对应Bishop的构造性数学的形式化。后来,Aczel把Myhill的集合论完善成一个形式系统,并称之为构造集合论,记为CZF。在此背景下,第一概述构造性数学的有关背景,并用实例展示它与传统数学的区别,说明了构造性数学的重要性;第二详细阐述构造集合论公理系统,说明它与其他公理系统的区别,为今后的研究工作——在构造集合论意义下构建非良基公理AFA的模型打下基础。
二、构造性数学
构造性数学是现代数学研究的一个重要领域。在数学的讨论中,常把能具体地给出某一对象或者能给出某一对象的计算方法者称之为可构造的。类似地,把能证实“存在一个对象x满足性质 P”的证明称为构造的是指能从这个证明中具体地给出一个满足性质P的对象x;或者能从此证明中,得到一个机械的方法,使其经有限步骤后,即能确定满足性质P的这个对象x。反之,也常把数学中的纯存在性证明称之为非构造的。非构造性的证明,是应用反证法来证明,即通过证明如果否定一命题则将导致矛盾,从而肯定原命题。这种通过矛盾进行证明是以亚里士多德逻辑的排中律为基础的。这种方法在近代数学中是常见的。人们把坚持主张“要证明一个数学对象存在,必须指出这个对象是怎么构造出来的”这种数学研究称之为构造性数学。构造性数学的重要意义在于构造性的研究不仅可以得出较为新颖、较为深刻的见解,而且构造性的成果更便于应用实际。
在非构造性数学的研究中,往往主要考虑对象的一些性质,如存在性、可能性等问题,不大关心如何求出解答、或将能行的方法予以有效的实现。然而,应用上对构造性数学要求更为迫切,一个工程师对于方程解的存在性和唯一性不会有太多的注意,而更关心一些典型的特解,或利用微扰或迭代方法找出近似解[3]。构造性数学要求远较非构造性数学严格,因为它得把存在的对象具体找出来,所以,构造性数学成立的每一定理对于非构造性数学也成立,并且每个命题的构造性证明绝对是这个命题的一个经典证明,因此,在这个意义上,构造性数学可以简单地看成非构造性数学的一个分支。事实上,早期以Borouwer为代表的直觉主义构造性数学是为了解决数学的奠基问题,然而后期以Bishop、Myhill等所代表的新方向,他们的构造性数学研究是在数学领域中,用普通逻辑于可编码的对象和递归函数。他们所关心的,不是去解决数学奠基问题,而是要用构造性方法来研究数学。他们把构造性数学看成经典数学的一个分支,在这个分支中所讨论的对象(个体或映射)都要求是可计算的[4]。
构造性数学不同于传统的经典数学,他的逻辑基础是直觉主义逻辑。在构造性数学中,数学家把“存在”严格解释为“可以构造”。为了进行构造性的工作,不仅需要把存在量词,而且要把全称量词和所有逻辑连接词都重新解释为一些指令,利用这些指令去构造关于逻辑表达式命题的证明。例如,在数学家们证明一个析取式P∨Q时,其中P和Q都是用形式或非形式语言表达的语法上正确的命题,就是要证明P或者证明Q。然而要构造性地证明P∨Q,则要把P∨Q进行自然的直觉主义解释,即不仅要确定P和Q中至少有一个是正确的,而且要确定到底哪一个是正确的。在这种直觉主义解释下,如果考虑一种特殊情形Q=¬P,即Q是命题P的否定,数学家们将面临一个严重的问题。要确定¬P就是要去证明P蕴含了一个矛盾(如0=1)。但是,在数学中,人们经常会遇到既不能确定P也不能确定¬P的情形,例如著名的哥德巴赫猜想:每个大于2的偶数都可以写成两个素数之和。尽管有很多大数学家对哥德巴赫猜想进行过努力,但至今还是既不能证明它也不能否定它。由此可知,在构造数学中,排中律并不普遍适用。这样,经典数学中的许多定理在构造性数学中将难以得到证明。在经典数学中,数学家把PVQ解释成¬(¬P∧¬Q),也就说“与P和Q都是错误的矛盾”。这种解释导致了存在量词的理想主义解释,即把∃xP(x)解释为¬x¬P(x),也就是说“与对每个x来说P(x)都是错误的矛盾”。这些解释都以亚里士多德逻辑的排中律(对每个命题P,要么P成立,要么¬P成立)为基础的。然而,这种解释是需要付出代价的,因为在这种理想主义的解释下产生的数学不能在计算模型(如递归函数论)中得到解释。为了进行构造性的工作,必须回到刚才的自然直觉主义的解释。在构造性数学中,对逻辑联接词和量词进行如下的解释:
∨:要证明 P∨Q,就必须要么有一个P的证明,要么有一个Q的证明;
∧:要证明P∧Q,就必须有一个P的证明,并且有一个Q的证明;
→:要证明P→Q,就必须找到一个算法,它可把P的一个证明转化成Q的一个证明;
上面这些工作主要是由 Brouwer、Heyting、Kolmogorov等发起的,所以这些解释被称之为BHK解释。为什么需要如此解释逻辑呢?一方面是由于想给出数学的计算性解释;另一方面是因为数学家想尽力用下面这种方式来发展数学,即如果一个定理断言具有某个性质P的对象x存在,那么这个定理的证明应该包含一个算法,这个算法构造出了这个对象x,并能证明它具有性质P。下面,举一个实例来说明构造性方法与传统非构造性方法的区别。
例1.中国剩余定理:若整数m1,…,mr互素,整数u1,…,ur已知,则存在唯一的整数 u∈[0,m1…mr],使得
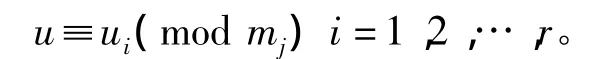
非构造性证明:作映射
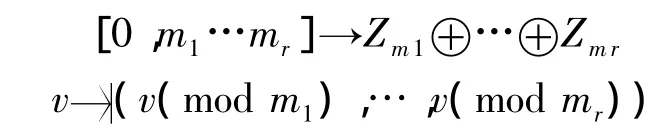
显然,这个映射是单射,且两边都有M=m1…mr个元素,因而两边是一对一的,定理得证。这是个很漂亮的证明,但是却不知道v具体是多少。
构造性证明:取Ni=(m1…mj…mr)φ(mj),其中 φ(mj)是欧拉函数,它等于(0,mj)中与mj互素的整数的个数,能够算出来。于是

这样,u1N1+u2N2+…urNr对M的余数就是要找的解。这个证明不但说明了解的存在,并且把这个解的具体值都求出来了,显然可以从这个证明过程中提取一个程序,使之在计算机上可以实现。
从上面的例子可以看到,构造性证明更直观、更具体,能让人切实感受到定理所描述的内容,从中可以提取一个计算机程序使其机械化;而非构造性证明却有某种模糊性。
三、构造集合论
Aczel利用 Martin Lof的类型论对CZF进行了解释,并证实了CZF的可构造性。Aczel的这种解释被认为是典范的,并且可以看作是用类型论给CZF建立了一个标准模型。
构造集合论为构造性数学提供了一个标准的集合论框架,它是诸多构造性数学集合论框架中的一种。构造集合论之所以如此与众不同是因为它使用的是经典公理集合论的一阶语言,并且没有使用任何具体的构造性思想。虽然CZF的逻辑是直觉逻辑,但其中不存在任何构造性概念和构造性对象。跟经典集合一样,这里只有集合这个概念。这就意味着构造集合论中的数学与经典集合论中的数学看起来非常相似。这样的优点在于如果遵守一些适当的原则,那么,通常数学的集合论表示的思想和惯例也能应用到构造性数学的集合论。而实际上,首先只需要遵守直觉逻辑中的逻辑推理原则,其次就是构造集合论中的集合论公理。
构造集合论CZF是经典集合论ZF的一个变体,所使用的是直觉逻辑。ZF的另一个变体被称之为直觉集合论IZF,IZF所使用的也是直觉逻辑。CZF与IZF的不同之处在于CZF避免了满非直谓词,而IZF没有。CZF和IZF的语言跟经典ZF系统一样,它们也仅包含二元谓词符号“∈”作为非逻辑符号。在直觉逻辑中,所有的二元联接词和量词(∧,∨,→,∃,∀)都是原始定义的,即没有一个是利用其他的联接词和量词来定义的。跟通常一样,可以利用蕴含和常项“⊥”(假)来定义否定,即¬φ是φ→⊥的缩写。在此前提下,来定义公理系统CZF和IZF。CZF的逻辑是直觉谓词逻辑,它与ZF公理系统的主要区别在以下几方面:在CZF中,分离公理仅对△0-公式成立,这样CZF有一个收集原则,而不是替换原则;在CZF中幂集公理被一个更弱子集收集原则所替代;另外,CZF使用集合的归纳原则,而不是基础公理。系统IZF是CZF的推广,它使用无限制的分离公理和幂集公理。
1978年,Aczel证明了如下结论:
CZF+EM=IZF+EM=ZF。
其中,EM表示排中律。这个结论说明了这三个公理系统之间的联系。
近年来构造性数学和构造集合论的研究甚为引人注目,构造性成果不断涌现,这就说明在某些情况下用这种观点来研究问题常常是大有裨益的。例如,数学家在构造性证明中提取一个程序,使之可以用计算机实现,从而实现数学机械化的宏伟目标。在许多情况下,构造性的方法与存在性的方法常常是同样地有效。构造性的研究不仅可以得出较为新颖、较为深刻的见解,而且构造性的成果更便于应用。众所周知,提供解答毕竟比纯存在性地证明有解要有意义得多。当一个数的存在能构造地证明时,那么这个数不仅在理论上,而且实际上也可以计算出来。联系到计算机科学已经蓬勃发展,这种构造性数学的研究更有其深远意义。
[1]张清宇.循环并不可恶——《Vicious Circles On the Mathematics of Non-Wellfounded Phenomena》评价[J].哲学动态,2005,(4).
[2]J.Barwise,L.Moss.Vicious Circles:On the Mathematics of Non-Wellfounded Phenomena[M].Stanford:CSLI,1996.
[3]吴文俊.复兴构造性的数学[J].数学进展,1985,(14).
[4]郝宁湘.构造性数学及其哲学意义[J].自然辩证法通讯,1997,(19).
