扭叶罗茨鼓风机转子型线改进设计与内流数值模拟分析

肖 芝，张小萍，翟旭军，王君泽

（1.南通大学 机械工程学院，南通 226019；2.江苏省畜牧兽医职业技术学院 机电工程系，泰州 225300）

0 引言

罗茨鼓风机是一种双转子压缩式机械，转子在不断的吸、排气过程中，进、排气腔的大小会发生周期性变化，由此产生不均匀气流作用于周围介质而引起压力脉冲，当基元容积（机壳与转子围成的区间）与排气口相连通时，回流冲击造成的压力脉冲更为剧烈，进而产生强烈噪音[1]，成为制约罗茨鼓风机发展应用的主要因素之一。研究结果表明，扭叶型罗茨鼓风机因其转子啮合方式可使基元容积不完全同时与排气口相通，延缓了回流时间，减少了回流强度，可明显降低噪音。然而，传统的扭叶型罗茨鼓风机效率相对较低，这使得它的应用明显受到了限制。长期以来，转子型线与机体结构的改进一直是专家学者们寻求设计高效率、低噪音罗茨鼓风机的主要途径，相关研究成果也不断涌现。王宏军、周朝晖[2]利用计算机辅助设计理论和齿轮啮合理论推导出扭叶转子啮合的数学模型，设计出由五段曲线组成的型线，改善了风机的密封性。张一健[3]对风机结构进行了探讨，得出异形排气口可有效减缓回流流速，降低噪音等。本文拟在比较、分析的基础上，对已有扭叶转子型线进行改进，提高面积利用系数，提升工作效率。同时，利用CFD（computational fl uid dynamics，计算流体动力学）技术对进行其内部流场的数值模拟，较真实地反映风机内部气流变化情况，并基于计算结果对风机的性能指标进行系统分析。

1 扭叶型转子型线的设计

1.1 传统扭叶转子型线的分析

目前扭叶转子型线常用的有外圆弧加包络线型、内圆弧加包络线型、渐开线型和摆线型四种。其中摆线型转子虽运行平稳，但面积利用系数低（最高0.406），故很少应用；其他三种型线转子面积利用系数相对较高(0.485～0.499)，而渐开线型转子运行平稳度相比圆弧包络线型转子较差，噪音较高，故在实际应用中多为圆弧加包络线型转子。本文拟对外圆弧加包络线型转子型线进行分析改进。

对于传统的外圆弧加包络线型线而言，径距比（即Rm/2a）是影响其面积利用率系数的重要因素（2a为两转子的中心距，Rm为叶轮外径），径距比越大，叶型就显得越瘦长[4]，其面积利用系数也就越高。根据文献[1]介绍，三叶圆弧包络线型Rm/2a的适用取值范围为：0.5589＜Rm/2a＜0.7358。当Rm/2a值小于0.5589时，会出现如图1（a）所示形状，此时的型线不存在凹凸并存，转子密封性差，而且叶型短胖，面积利用系数低，一般很少采用。当Rm/2a值大于0.7358时，则在G0点处出现角点（如图1（b）所示），这时面积利用系数虽有所提高，但出现干涉，去除角点后啮合时密封性能也很差，无法使用。基于以上分析，本文拟对此型线进行改进，以渐开线代替角点处的畸形型线。

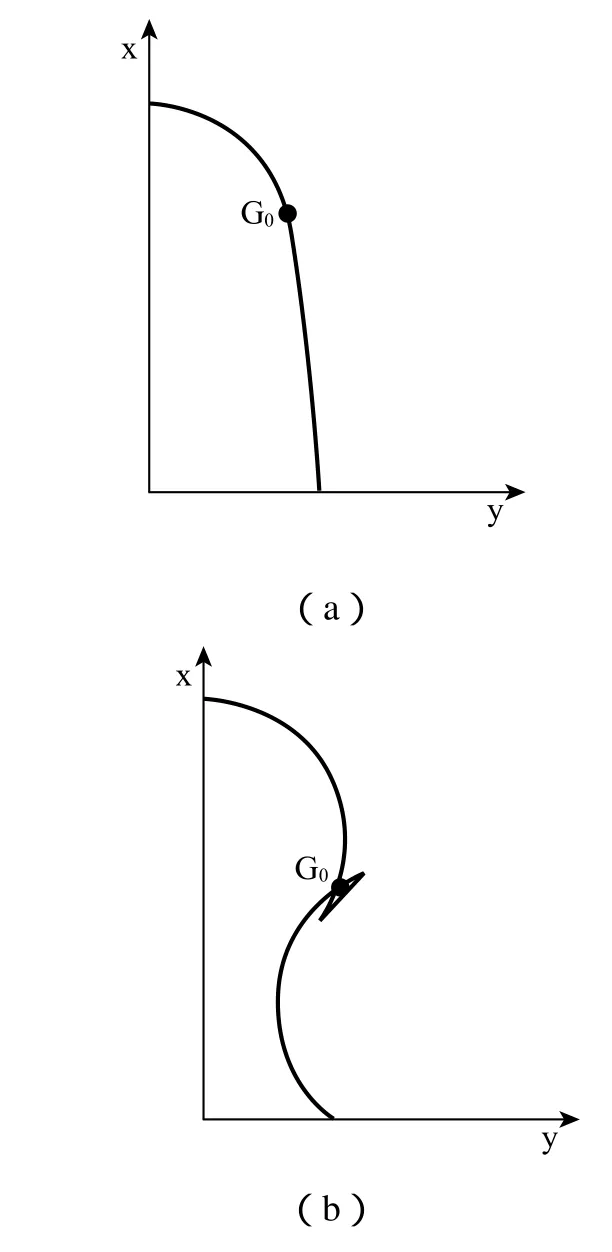
图1 径距比值对型线形状的影响

1.2 型线方程的确定

如图2所示，假设转子1绕着其中心O1顺时针转动α角，转子2绕着其中心O2逆时针转动相同的角度。将转子1、转子2和机架固定，转子间的相对运动可看作整个机构绕着O1逆时针转过角，其中两个转子在G点啮合，两个节圆在P点相切，点P为O1和O2的中点。两共轭曲线在G点的公法线必经过点P，并经过O2转子叶峰圆弧圆心F2，GF2即为叶峰圆弧半径记为r，F2O2为叶峰圆心到叶轮中心的距离记为b。过O1作GF2的平行线，交O2F2的延长线于点H，O1H与O1x轴的夹角为β。过点O2作O1Y轴的平行线，交O1X轴于点K，过点F2作O1X轴的平行线交O2K于点L，且点G在F2L的垂足为点M，过点H作O1X轴的平行线交O2K的延长线于点J,作O1X轴的垂直线HI，由其中的几何关系可得出圆弧段型线的参数方程为：

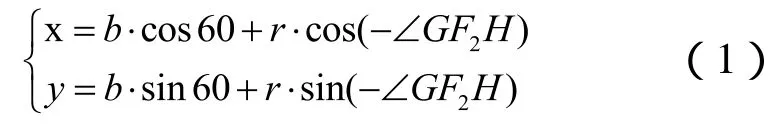
由图2可知：

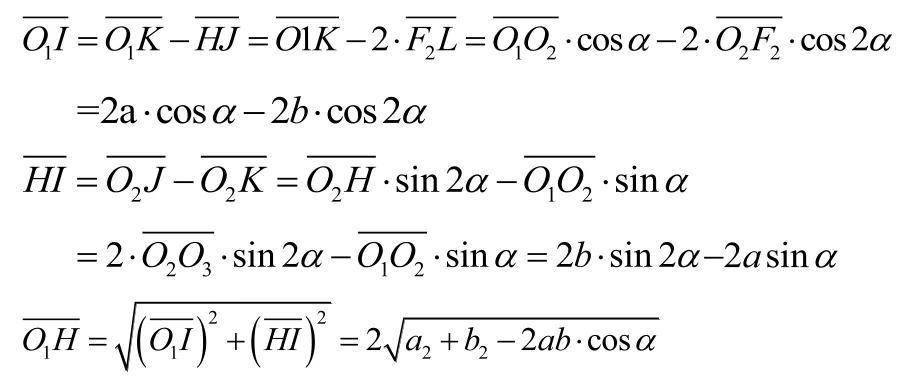
得：

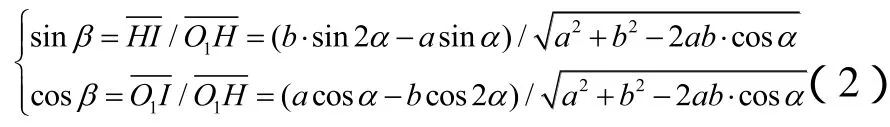
因为O1H//F2G，则,啮合点 G(x1，y1)在坐标系X1O1Y1中的坐标为：

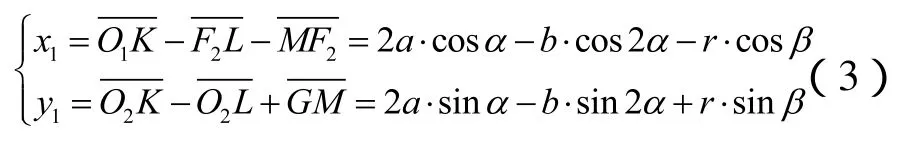
此为圆弧包络线段的型线参数方程。

图2 转子啮合示意图

对于渐开线参数方程的确定，首先要计算出上述圆弧与包络线的参数方程中的参数值。图3为改进后的型线：BC为渐开线，GB为圆弧包络线，CH为圆弧，渐开线的基圆半径r1即为包络线终点到转子中心O的距离，包络线的终点即为渐开线的起点，渐开线的终点即为圆弧的终点，由此可得渐开线参数方程：

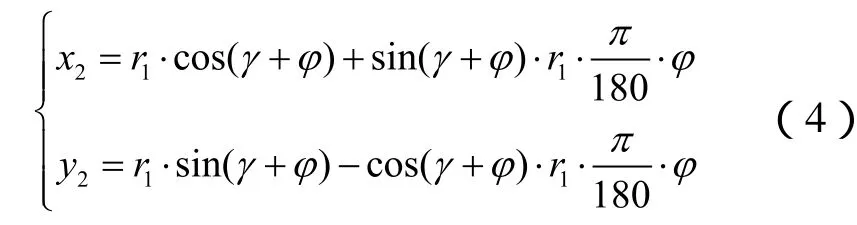
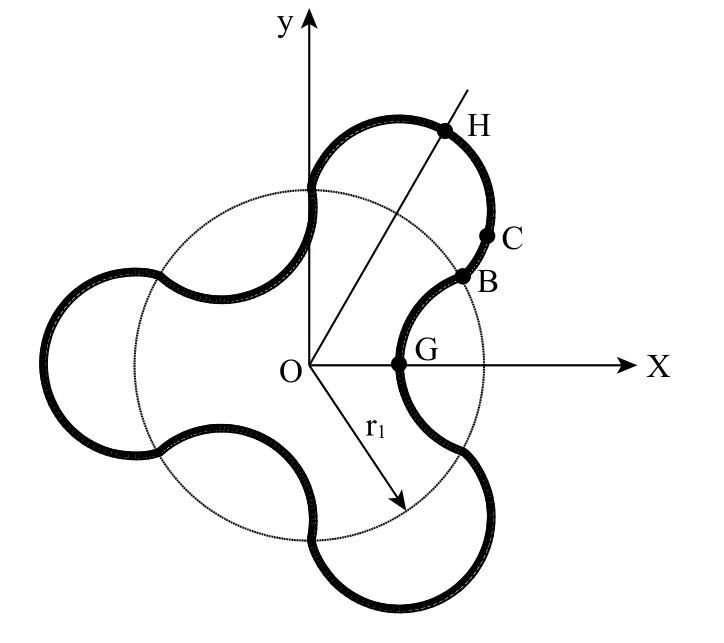
图3 改进后的转子型线组成

以中心距2a=84为例，其中，Rm/2a=0.7526，由式 (1)～ 式 (4)可得到：α=2.1625，β =71.83431，渐开线基圆半径r1=41.24，渐开线展开角度为φ=42.2659。这样的参数设计打破了径距比Rm/2a值的限定，既可以提高面积利用系数，又避免了出现角点的尴尬。

2 参数化建模与型线特征分析

根据上述改进的型线方程，可在Pro/E平台上建立其参数化三维模型。扭叶型鼓风机一般为三叶转子，且扭转角为60°，两啮合转子的扭转方向相反。图4（a）为其装配示意图，图4（b）为（a）位置的全局干涉检测结果，显示转子机构在旋转的各个位置均无干涉发生。

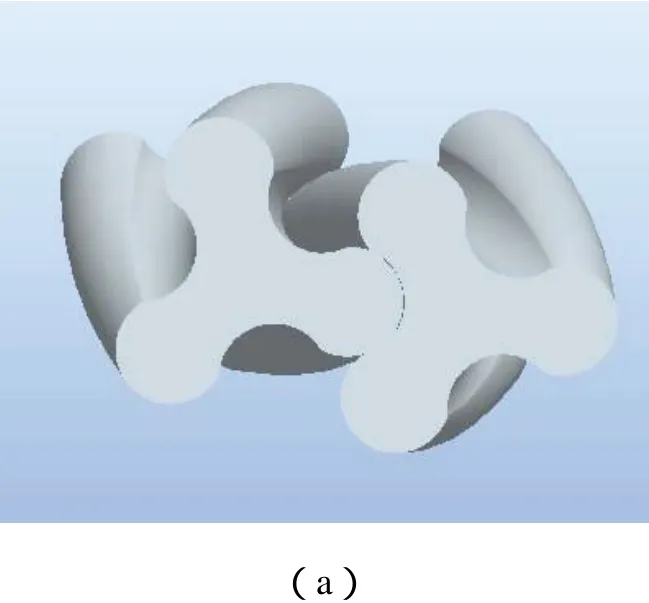
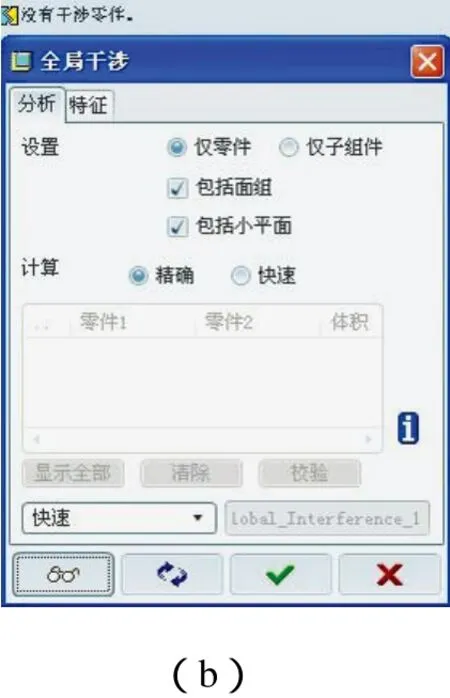
图4 转子三维模型及干涉检测结果

设定转子外圆半径绕转子中心旋转一周所扫过的面积为S0，转子横截面积为S1，则面积利用系数Q=1-(S0-S1)/ S0。令中心距相同且径距比（Rm/2a）为最大值，通过参数化建模在Pro/E平台上可快速测量出各型线转子的相关几何参数，如表1所示。

从表1中可以看出改进后的转子型线引用渐开线进行拐点处的过度，不仅避免出现干涉现象，保证了密封性，且突破了传统圆弧加包络线叶型径距比的适用范围。在中心距一定的情况下，改进后的型线转子外圆直径相对较大，转子更显瘦长，从而提高了面积利用系数，提升了工作效率。表1显示改进后的型线转子其面积利用系数比传统圆弧包络线转子高出0.02，因为罗茨鼓风机多为24小时连续工作，因此提高0.02对企业也有着较好的实际意义。

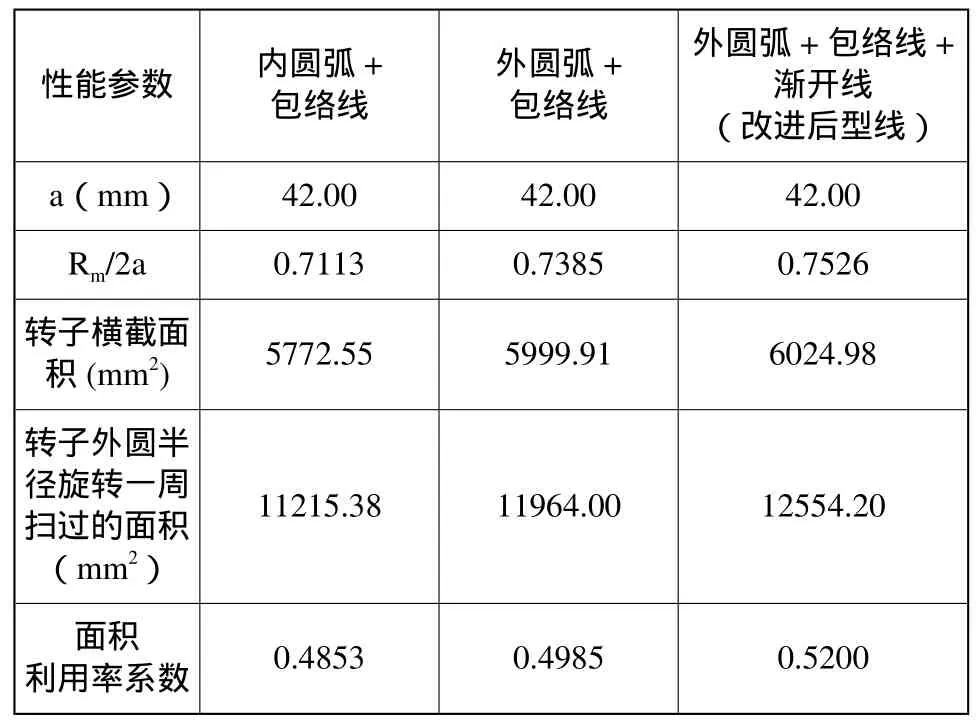
表1 不同型线参数对比

3 CFD技术与内流数值模拟

3.1 CFD技术与Fluent软件

CFD技术是利用电子计算机对固体边界的内外流场进行数值模拟和分析的学科，它以流体力学为基础，数值计算为工具，通过求解三大控制方程或附加方程(即连续性方程、动量方程和能量方程)来获得所要研究的相关参数，费用低、周期短、成本低，可以模拟多种复杂流场，考察流体的细微结构及其运动过程[5]。随着计算机技术的不断发展，其应用已从最初的航空领域扩展到包括风机在内的多个领域，利用Fluent对离心式风机、旋涡式风机等旋转式机械进行内部流场的数值分析的报道已不鲜见[6,7]，为罗茨鼓风机的数值模拟提供了一定的借鉴作用。目前CFD软件众多，有 Phoenics、CFX、STAR-CD、Fluent等， 而Fluent应用最为广泛，它是用于模拟和分析复杂几何区域内的流体流动的专用软件，基于CFD软件群思想，针对各种复杂流动的物理现象，采用不同的离散格式和数值方法，在计算速度、稳定性、和精度等方面达到最佳匹配的状态下求得计算结果。本文拟采用Fluent作为求解器对罗茨鼓风机内流场进行数值模拟。

3.2 计算过程及相关参数设定

3.2.1 计算模型的建立与网格划分

利用Fluent软件对罗茨鼓风机内流场进行数值模拟的求解简易流程图如图5所示。根据上文提供的转子型线，建立转子的二维计算模型。本次数值模拟拟运用动网格技术，所以网格划分采用非结构性网格方法、三角形网格类型，其网格数为：57558，在转子与墙体边界处产生最大扭曲度网格，其扭曲度为0.519459。

动网格技术则采用局部网格再生成和弹性光滑模型，动网格的参数设定通过编辑prof i le文件来实现，以叶轮转子为动网格的基本参照，相对转子重心的角速度为1500n/min，周期则为0.04s，两个转子均定义为刚体。由于本文中罗茨鼓风机要实现的运动是两个转子相互旋转，运动形式相对简单，其左右转子prof i le编辑为:

左转子：

((left 3 point)

(time 0 1 60)

(omega_z 157.075 157.075))

右转子：

((right 3 point)

(time 0 1 60)

(omega_z -157.075 -157.075 -157.075))

其中，left和right为速度名，3 point为所取速度变化点数，由于两转子为恒速转子，速度变化点可任意取，time后为所取点的时刻值，omega_z后为所取点绕z轴的角速度。本文中叶轮转速 1500r/min，可得角速度为157.075rad/s。

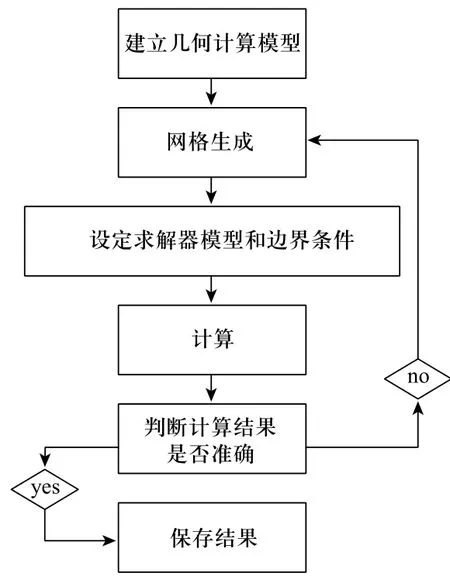
图5 Fluent求解简易流程图

图6 二维计算模型及其网格划分示意图

3.2.2 求解器模型的设定

罗茨鼓风机内部流体运动属于湍流，本文运用非稳态湍流模型对其进行数值模拟。在风机的数值分析中，标准k-ε模型、RNG k-ε模型这两种湍流模型最常用[8]，但 RNG k-ε模型在解决旋涡问题上相比标准k-ε模型显的更好，且 RNG k-ε模型中的耗散率ε方程比标准k-ε模型多加了一个约束条件，有效的改善了精度，因此本文选择RNG k-ε模型。

3.2.3 边界条件的设定

边界条件设定是CFD问题计算的必要条件，本次分析模型包括壁面边界与进出口边界，介质为空气，属性按理想气体进行设定。固壁区域内的速度和温度采用壁面函数方法，环境及固体边界温度为恒温25℃。进出口边界分别为压力进出口，给定进出口压力初始条件：绝对压力进口（103825Pa）、绝对压力出口（108825Pa）。

3.3 计算结果与分析

图7为罗茨鼓风机进气口质量流量变化曲线图，由图中可看出在f l ow time 0.005—0.045s的一个周期内，流量随时间出现了6次谐波变化，频率正好是罗茨鼓风机叶片的数目，这是由于转子相互啮合所产生的，且流量的重复性比较好，计算结果符合实际情况。

罗茨鼓风机叶轮之间、叶轮与机壳之间具有微小间隙，鼓风机内部难免会出现回流、涡流现象，对此数值模拟可较为真实的反映。图8分别为0.01与0.02时的速度矢量图，如图所示：在转子之间、转子与机壳壁面之间的缝隙都出现了回流，且回流速度相对风机内部其它区域的速度较高，这是由一个基元容积内压强与排气口处的压强都高于进气口处的压强而导致的。在排气口处，与叶轮相临近的机壳壁面附近产生了涡流现象，其发生原因应主要是壁面附近低速气流与高速的出排气流的相互参杂，同时还有回流气体流动方向与主气体流动方向不一致。回流与涡流是造成罗茨鼓风机噪音大的一个重要原因，所以在罗茨鼓风机的降噪设计中如何减少排气口的回流与涡流和降低回流与涡流强度是关键。

4 结束语

针对传统扭叶转子型线面积利用系数都相对较低的不足，分析了外圆弧包络线型线，并对其进行改进，解决了高径距比时存在的干涉、密封性差问题，保持扭叶转子风机低噪音优势的同时，提高了面积利用系数，提升了工作效率。利用Fluent软件，数值模拟出改进罗茨鼓风机进排气过程中机腔内部气流的流动情况，得到进气口质量流量、气体流速随时间的变化规律，及其对流场中回流、涡流现象进行了分析，为提高罗茨鼓风机的设计效率和改进罗茨鼓风机的性能提供依据。

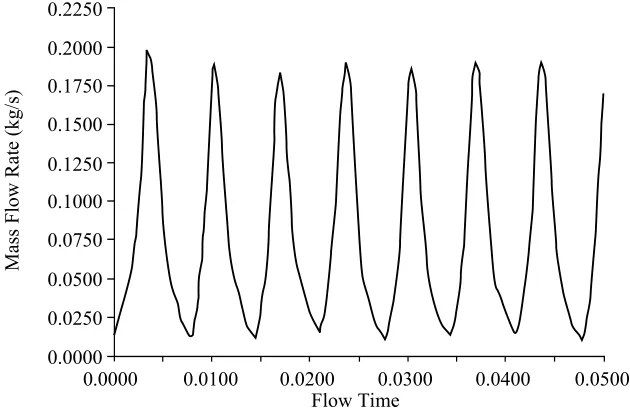
图7 进气口质量流量随时间变化规律曲线图

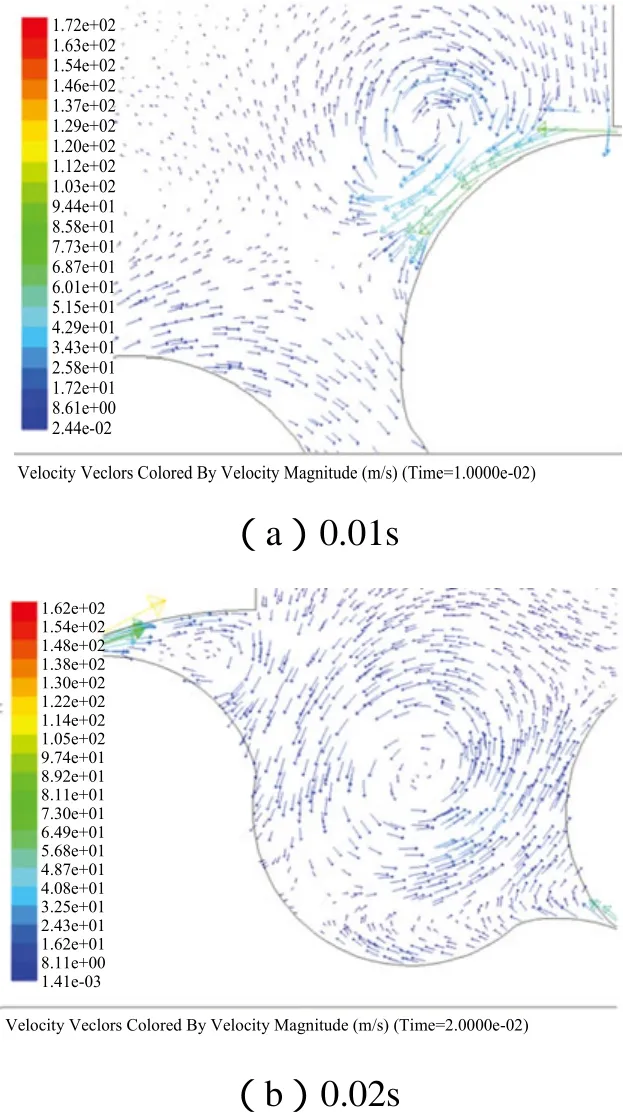
图8 速度矢量图

[1] 苏春模. 罗茨鼓风机及其应用[M]. 长沙: 中南工业大学出版社, 1999.

[2] 王宏军, 周朝晖. 对称螺旋转子风机转子型线研究和设计[J]. 机电设备, 2002(1): 1-4.

[3] 张一健. 罗茨鼓风机创新结构设计及噪声治理[J]. 通用机械, 2007, (3): 77-81.

[4] 彭学院. 罗茨鼓风机渐开线型转子型线的改进设计[J].风机技术, 2000, (3): 3-5.

[5] 朱红钧, 林元华, 谢龙汉. fluent流体分析及仿真实用教程[M]. 人民邮电出版社, 2010.

[6] Eui-Yong Kwon, Nam-Hyo Cho. Experimental Study on the Mean Flow Characteristics of Forward-Curved Centrifugal Fans[J]. KSME International Journal, 2001, 12(15): 1728-1738.

[7] John Vande Voorde, Jan Vierendeels, Erik Dick.Flow simulations in rotary volumetric pumps and compressors with the factitious domain method[J]. Journal of Computational and Applied Mathematics, 2004(168): 491-499.

[8] 王孚懋, 等, 低噪声罗茨鼓风机的结构设计与内流数值模拟研究[J]. 山东大学学报, 2010, 29(6): 55-60.