基于差分进化的制造业移动机器人路径规划方法

张诗淋

（沈阳职业技术学院，沈阳 110045）

0 引言

科技的进步能够改善人类的生活质量以及提高生活的便利性，因此机器人的相关研究一直是许多科学家致力研究的方向。随着人工智能、机器视觉与微处理器的迅速发展，自动化的应用也越来越普遍，智能机器人的相关研究也越来越广泛，大至太空探索，小到制造自动化及服务型机器人，处处都可以发现智能机器人成功的应用。

目前，关于移动式机器人的应用已经相当的广泛。移动式机器人也可以在日常生活中给予人们越来越多的帮助，在日本娱乐型机器人的研究发展更是迅速。自从1999年Sony 公司发布的AIBO机器狗大卖之后，2000年又开发出多款拟人化的机器人，如日本本田发布会爬楼梯的Asimo，Sony发布了会随音乐跳舞和与人对话的QRIO机器人等。Roomba吸尘机器人由麻省理工学院（MIT）人工智能验室研发，由iRobot公司制造。它主要用在居家清洁上，能像吸尘器一样自动清理地板，碰到墙壁或障碍物，也能轻巧弹开。另外，日立公司发布了功能与Roomba 类似的家用清洁机器人，机器人可以移动至房间的角落，可动吸尘口就能够自动伸出进行清扫。

在各种应用中，移动式机器人必须在特定环境下完成指定的动作，因此到达目标的路径规划相当重要[1]。移动机器人的路径规划决定了移动机器人一切的行动，路径规划的策略包括了路径的规划及导航、寻找最优的路径、以及闪避障碍等。移动机器人的路径规划与导航是控制移动机器人行动中最重要的研究内容。路径规划的目标是在最短时间内，使用最短的距离朝着目标标地物前进，且不能与其他障碍物相互碰撞。在移动机器人完成各种任务时，无人导引控制的技术起着关键的作用，也是机器人的研究上一个重要的指标。根据无人导引控制的技术，可将机器人分类为有轨式移动机器人与无轨式移动机器人两类。有轨式的引导技术研究发展已经成熟，目前大多研究致力于无轨式移动机器人。

本文以制造业中的无轨式机器人为例，以多道加工工序中的螺丝安装为任务，提出一种基于差分进化算法的移动式机器人的最优路径规划方法，使得机器人在各个加工床上螺丝安装的加工时间最短。实验结果显示，在20个加工床的情况下，该方法能够得到满意的结果。

1 移动机器人路径规划

在移动机器人的移动路径上，为了在最小时间完成所有的加工工序，随时都要凭着实时的环境信息，来更新机器人的位置及目标点之间路径。首先描述本文的移动机器人规划问题：给定n个加工床{b1,b2,…,bn}，它们存在于一个二维地图上，我们的目的是机器人经过所有的加工床，满足并避免重复走过相同的路径，即寻找一条从起点到目标点的最短距离路径：

其中，di,j是加工床bi,bj之间的距离。

目前求解该问题的方法大多集中在启发式解法。这些启发式解法可以分成如下四种[2,3]。

1）穷尽搜索法

我们以最直观的遍历方法一一计数来求解最优路径，亦即找出所有可能的路径，计算每条路径的成本后，找出其最小者。如果有n个加工床，那么共有(n-1)!条路径。若n=26，则有25! 条不同路径。假设计算机每秒可计算100条路径的成本，求出所有路径的成本就需时五千亿年，这样造成较低的计算效率。

2）分支界定法

最优路径问题的解可以树(tree) 表示，因此我们需找出最短距离路径的树，分支界定法搜寻此最优解的思想为：将树形不断分支，但随时以问题的条件限制分支的继续，即如果知道最优解不会出现在通过此点的路径，则不必继续分支，因此所需搜寻的路径将大大减少。

3）动态规划

以动态规划求解，其计算复杂度 (computational complexity) 仍然呈指数上升，对目前及未来的计算机而言，一个计算复杂度呈指数上升的问题，在 n相当大时仍无法解决。

4）近似法

既然最优路径问题是个难题，我们可以退而求其次找一个近似解，这种解法从直观而来，称为最近邻法 (nearest-neighbor method )。 例如，从加工床 1 开始，先找最近 1 的加工床 d1，次找最接近 d1 的加工床 d2，再找最接近d2 的加工床d3，，直至找出所有的加工床，将最后一个加工床与 1 连接，即得所求的路径。

2 基于差分进化算法的路径规划

差分进化算法( Differential Evolution Algorithm，DEA)是 R.Storn,及 Price,K.在 1997 年第一次提出[4]，它是一种以群体为基础，来进行空间中的随机搜寻的优化方法。相比经典的遗传算法，差分进化算法具有实现简单，参数少，收敛速度快的优势。而且不管初始解的好坏，它都可以找到全部可行域的最优解。

差分进化算法在搜寻空间中，每一个向量代表一个解，称为解向量，每一个解向量在搜寻空间中各自拥有方向和大小，解向量不用解向量之间的差距，使每一个解向量不断地往最优解方向前进，以达到最好的位置。差分进化算法如图1所示。

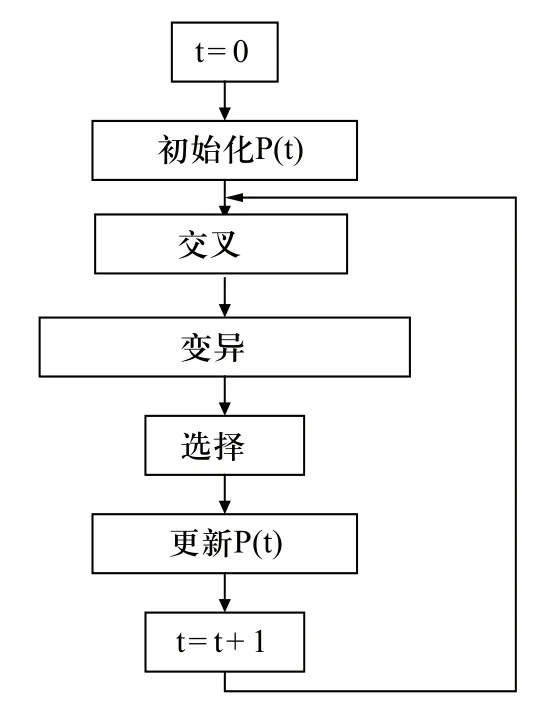
图1 差分进化算法步骤

差分进化算法在解向量的进化中，经过迭代的方式，调整出最正确的参数解，来更新种群，演化的过程中包括了变异、交叉及选择方法。变异是由三个不同的解向量产生一个差分向量。交叉是复制差分向量中的某段位置来覆盖父代中相对应的位置，覆盖的长度由一个解变量决定。选择是评估父代与子代的适应值，两者之中删除较差的保留最优的。一直重新配置，最后差分根据目标函数值找出最优解。

在差分进化算法中，其每个候选解(candidate solution)即为一个解向量，变异策略是在差分阶段找到的解向量中随机选取三个不同的解向量，彼此之间相互交叉运算，得到一个新的个体，这个新个体又称为差分向量Dv (Difference vector)：

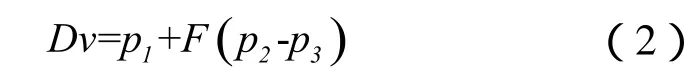
其中，p1, p2, p3为种群P(t)中的个体，F为比例系数。计算后得到的差分向量Dv不再是整数，我们按照值的大小进行排序，将所得到的序号来代替差分向量Dv，作为变异后的个体。类似的，交叉之后也会产生类似的无效解，也是按照值的大小进行排序，将所得到的序号来代替交叉后的解向量。在有相同数值的情况下，随机选择先后顺序。差分进化算法的目标函数值定义为式(1)所示。基于差分进化的路径规划算法步骤如下。

1）初始化代数初始化：t=0；初始化种群P(t)，种群中每一个个体代表一个可行的路径；

2）按式(2)执行个体变异操作，生成新的P(t)；

3）执行个体交叉操作，生成新的P(t)；

4）按照式(1)计算目标函数值，评价群体P(t)的优劣，选择目标函数值最小的个体；

5）停机条件判断：当满足停机条件时，输出当前最优个体，否则继续；

6）更新 P(t)，t=t+1，转到 2）。

3 实验与结果

考虑20个加工床的问题，差分进化算法中种群的规模为100，将差分进化算法中种群的每个个体编码为一个长度为20的向量。F设为0.2，最大迭代次数设为300。由差分进化算法确定得到的最优路径如图2所示，其对应的最短距离为219米，时间为298秒。从图2中可以看出：在时间上与路径距离上都还是满意的。

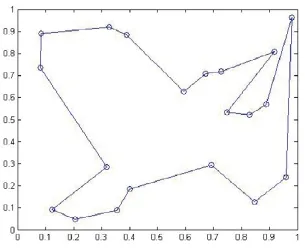
图2 差分进化算法得到的最优路径

4 结论

如何在最短时间内，使用最短的距离让移动式机器人朝着目标地前进，这是路径规划的基本目标。本文以制造业机器人为例，以多道加工工序中的螺丝安装为任务，提出一种基于差分进化算法的移动式机器人的最优路径，使得机器人的制造加工时间最短。实验结果证明了该方法的有效性

[1] M.S. Lee, M.J. Jung and J.H. Kim, “Evolutionary programming-based fuzzy logic path planner and follower for mobile robots,”[C], Proceedings of the 2000 Congress on Evolutionary Computation, vol. 1, pp. 139 - 144, 2000.

[2] 涂序彦. 人工智能: 回顾与展望[M]. 北京: 科学出版社,2006.

[3] 阎平凡, 张长水. 人工神经网络与模拟进化计算[M]. 北京: 清华大学出版社, 2000.

[4] R. Storn, and K. Price, “Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces Storn,” Journal of Global Optimization[J], 1997,11(4): 341-359.