自适应衰减记忆UKF 算法在三维水下目标跟踪中的应用

王满林

(海装重庆局，重庆 400023)

声纳实时量测跟踪水下目标是非线性滤波应用领域中一个高度复杂的问题，这主要是因为测量方程为非线性的。纯方位被动跟踪技术是目标跟踪的重要研究领域之一，其所要解决的是如何利用被动声纳观测到的目标方位信息来估计目标的运动参数，如距离、航速、航向等参数。

解决非线性滤波问题最为普遍的方法是扩展卡尔曼滤波器。但是该方法只适用于弱非线性的系统，对于强非线性系统，很容易导致发散［1-2］。EKF 算法则是KF 算法的非线性扩展，是一种递推算法，由于在每个采样时刻对估计状态矢量的线性化导致协方差矩阵产生畸变，容易使EKF 发散。卡尔曼滤波是增长记忆滤波，一般情况下它给出了一个随着观察资料的积累精度不断提高的估计。估计误差协方差的范数随着时间的增长不断减小，因此新的观察资料对修正状态估计的作用逐渐减弱。但是，实际上系统动态模型的变化规律是很难在事前完全知道的。这样，一方面这些系统的参数在变化，另一方面，在递推过程中还是把这些已经变化了的参数当作精确值来进行运算。于是，计算的误差协方差阵的范数随着时间的增长不断减小，而实际误差协方差却不断增大，最后导致滤波器发散。由于新近的观察资料含有变化了的系统动态模型的较多信息，在滤波器中须增强这些新观察资料对修正状态估计误差的作用，降低老的观察资料的地位。有限记忆和衰减记忆滤波器就是基于这一考虑而提出的防止滤波器发散的方法［3-4］。

最近，研究人员提出一种新的用于解决非线性滤波问题的滤波器，他们将这种滤波器称为Unscented 卡尔曼滤波器(UKF)［5-6］。其实现原理为:在原先状态分布中按某一规则取一些点，使这些点的均值和协方差等于原状态分布的均值和协方差;将这些点代入非线性函数中，相应得到非线性函数值点集，通过这些点求取变换后的均值和协方差。由于这样得到的函数值没有经过线性化、没有忽略其高阶项，因而其均值和协方差的估计比EKF 方法要精确。

UKF 虽然能够克服EKF 存在的一系列问题，改善了系统线性化误差，但并没有明显改善卡尔曼滤波器容易发散的问题，在实际应用时，UKF 对滤波初始值也比较敏感，系统噪声相关信息的不确定性以及状态模型扰动等都会影响UKF的滤波精度。针对UKF 存在的问题，本文提出了一种自适应衰减记忆UKF 算法(adaptive fading memory UKF，AFMUKF)。

1 问题描述

本文考虑迪卡尔坐标系下三维双基阵纯方位问题。假定目标是作匀速直线运动的，用X(t)=［x(t)，y(t)，z(t)，vx，vy，vz］T表示目标的状态，X0i(t)=［x0i(t)，y0i(t)，z0i(t)，v0x，v0y，v0z］T(i=1，2)表示基阵1 与基阵2 的运动状态。则系统状态方程为

其中

测量方程为

其中βmi(k)为双基阵的2 个声纳在第k 个采样时刻(采样周期为T)所提供的观测方位，

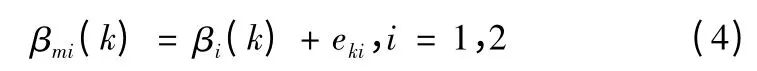
其中βi表示真值方位，

αm1(k)为基阵1 对目标观测的俯仰角，

其中:

双基阵纯方位问题就是，根据测量得到的方位序列来估计目标的运动要素。

2 UKF 滤波算法

2.1 UT 变换

Unscented 卡尔曼滤波器(UKF)也是一种递归式贝叶斯估计方法，它利用Unscented 变换(unscented transformation，UT)方法，用一组确定的取样点来近似后验概率。但是UKF不必线性化非线性状态方程和观测方程，它直接利用非线性状态方程来估算状态向量的概率密度函数。

Unscented 变换是计算进行非线性传递的随机向量概率的一种方法，它是基于这样一种考虑:近似一种概率分布比近似一种任意的非线性方程或者非线性变换要容易的多［5，6］。设x 是nx维的随机向量，g:Rnx→Rnz是一非线性函数z=g(x)，考虑将x 通过非线性函数g 传递，假定x 的均值和协方差分别为和Px。为了计算关于z 的统计量，首先选择2nx+1 个带有权值的样本点(也称SIGMA 点)Si={Wi，χi}，，使其能够完全获取随机变量x 的真实的均值和协方差。SIGMA 点的选择以及权值的确定是根据以下方程:

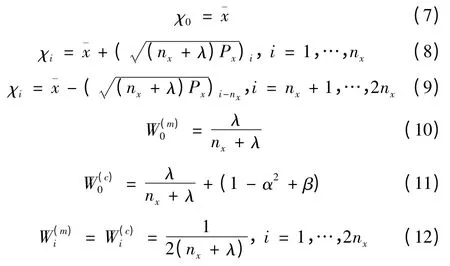
其中λ=α2(nx+κ)-nx是一个尺度调节因子，α 决定了选择的SIGMA 点在其均值¯x 附近的分布情况，通常将α 设置为一个很小的正值(如0.001)。κ 是次级尺度调节因子，通常设置为0，β 是用来结合关于x 的分布的先验知识(对于高斯分布，β 的最佳取值为2是矩阵(nx+λ)Px平方根的第i 行，Wi表示第i 个SIGMA 点的权值，且满足∑Wi=1。是用来计算均值的权值是用来计算协方差的权值。

将每个SIGMA 点通过非线性函数向前传递，

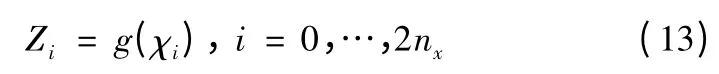
通过计算可以得到z 的均值和协方差的估计，

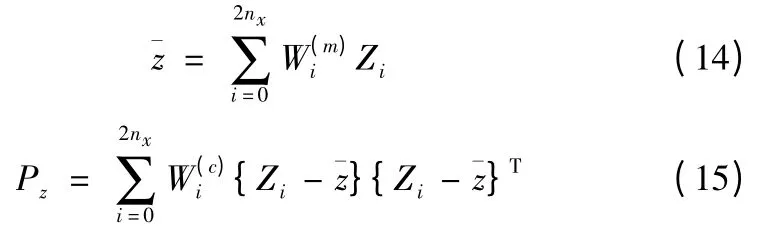
2.2 UKF 算法原理及步骤

根据以上的U 变换，可得纯方位条件下的UKF 算法，假设k-1 时刻的状态及相应协方差的估计分别为和其计算步骤:

1)利用初始状态估计，设定最初的2nx+1 个SIGMA 点

2)利用过程模型变换这些SIGMA 点

3)计算预测估计值

4)计算预测协方差

5)通过测量方程计算测量值

6)计算预测测量值

7)计算新息方差

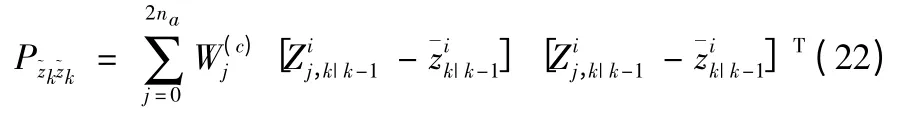
8)计算协方差P~xk~zk

9)计算Kalman 增益

10)更新误差协方差

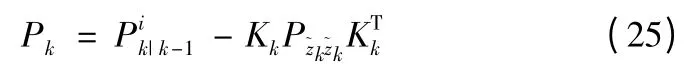
11)更新状态

3 AFMUKF 算法

采用衰减记忆滤波器，在UKF 的基础上引入衰减因子，构成衰减记忆UKF 滤波器(FMUKF)，采用Tarn 和Zaborsky提出的一种简单实用的引入衰减因子的方法［7］。FMUKF 的递推关系和UKF 的不同之处在于，在式(19)中加入了衰减因子S，使式(19)变为

将UKF 计算步骤中的式(19)替换为式(27)即可得到衰减记忆UKF 算法［8］。但在仿真中我们发现，衰减因子的选取会对滤波结果产生很大影响，引入衰减因子后的滤波将使估值的方差增大，且衰减记忆滤波的精度随S 的增加而降低，在一些情况下可能会发生异常，甚至导致滤波发散。为此，在加入衰减因子的基础上，再引入一个自适应因子，将式(22)、(23)和(25)变为

式中αk为自适应因子，0 ＜αk≤1。

合理的自适应因子能够自适应地平衡状态方程与观测信息的权比，还能够控制状态模型扰动对滤波解的影响。αk构造为［9-10］:

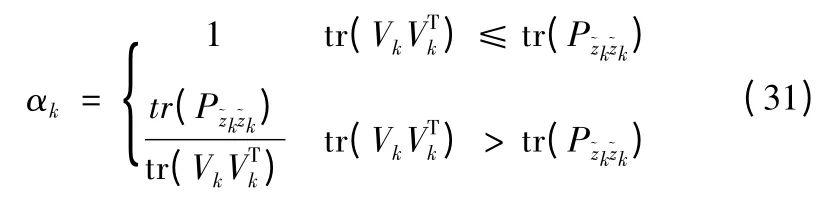
其中Vk为预测残差，

由上述分析可知，当初值选取不合理或模型存在异常扰动时，αk将小于1，即预测信息对滤波解的贡献将尽量小;当预测信息明显异常时，tr(VkVTk)将非常大，αk则将接近于0，即预测信息被完全弃用，从而有效控制了模型误差对滤波解的影响。

4 仿真实验

传统的跟踪滤波算法扩展卡尔曼滤波器解算三维空间运动目标存在一个明显的缺陷是Jacobian 矩阵推导的复杂性。与EKF 中采用Jacobian 矩阵进行线性化不同，UKF 通过一组仔细选择确定的采样点来捕获系统的相关统计量，将非线性映射直接作用于各采样点。因此，本文对三维水下运动目标采用UKF 和AFMUKF 两种算法进行数学仿真。

假设一水下运动目标开始在水下-200 m 处作匀速直线运动，100 s 后持续向上爬升，200s 后停止爬升，继续作匀速直线运动。仿真初始条件为:采样间隔T=1 s，方位角、俯仰角观测误差方差均为1°，两基阵位置分别为(-1000，0)、(1000，0)，目标初始状态为［- 2 000，4 000，- 200，20，-20，0］T，滤波器初始化为

x(0 | 0)= ［-4 000，7 000，-250，10，10，10］T

P(0 | 0)= diag(10 000，10 000，10 000，10，10，10)

对于AFMUKF 算法，衰减因子S=1.02。对2 种算法分别进行30 次Monte-Carlo 仿真实验，仿真结果如图1 ～6所示。

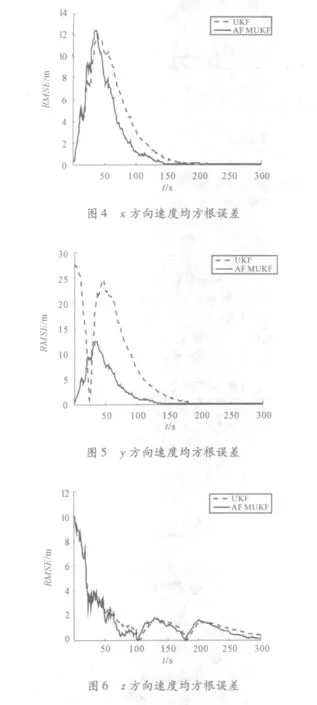
从仿真结果可以看出，在仿真的初始时刻，滤波器都有较大的初始偏差，这是由于初始估值造成的。随着滤波的进行，AFMUKF 算法能很快地收敛到真值位置附近，并保持较高的滤波精度。AFMUKF 算法较UKF 算法提高了解算精度及收敛速度，且增强了数值稳定性。究其原因，主要在于AFMUKF 算法加大了对新测量值的利用权重，减少了对陈旧测量值和初始估值的依赖，并且具有一定的自适应能力，能够实时检测出滤波中出现的异常，有效控制了初始值偏差及模型异常扰动误差对滤波解的影响。

5 结束语

由于UKF 能有效处理系统方程非线性程度大的情况，所以在处理被动目标跟踪等典型的非线性问题时性能较好，然而，UKF 虽然改善了系统线性化误差，但并没有明显改善卡尔曼滤波器容易发散的问题，为此，本文在UKF 中引入衰减因子及自适应因子，对纯方位目标跟踪采用自适应衰减记忆UKF 算法。理论分析和仿真结果均表明，AFMUKF 算法的滤波精度、稳定性、收敛时间等都明显优于UKF 算法。

［1］Aidala V J.Kalman filter behavior in bearings-Only tracking applications［J］. IEEE Transaction on AES，1979，15(1):29-39.

［2］杜选民，姚蓝.多基阵联合的无源纯方位目标运动分析研究［J］.声学学报，1999，24(6):604-610.

［3］LU P，ZHAO L，CHEN Z. Memory-attenuated least squre filtering and its application［C］//Proceedings of the 6thWorld Congress on Intelligent Control and Automation.Dalian:［s.n.］，2006:1483-1486.

［4］LEE T S.Theory and application of adaptive fading memory Kalman filters［J］.IEEE Transactions on Circuits and Systems，1988，35(4):474-477.

［5］Julier S J，Uhlmann J K.Unscented filtering and nonlinear estimation［J］.Proceedings of the IEEE，2004，92(3):401-422.

［6］Wan E A，Merwe R.The unscented kalman filter for nonlinear estimation［C］//Proceedings of International Symposium on Adaptive Systems for Signal Processing，Communications and Control.Alberta:［s.n.］，2000，153-158.

［7］TARN T，ZARBOSKY J.A practical non-driving filter［J］.AIAA Journal，1970，8(6):1127-1133.

［8］罗涌，钟洪声.一种改进的UKF 算法在目标跟踪系统建模中的应用［J］.遥测遥控，2008，29 (1):55-58.

［9］YANG Y X，GAO W G.An optimal adaptive Kalman filter［J］.Journal of Geodesy，2006，80(4):177-183.

［10］GAO W G，YANG Y X，CUI X Q.Application of adaptive Kalman filtering algorithm in IMU/GPS integrated navigation system［J］. Geo-Spatial Information Science，2007，10(1):22-26.

［11］张林琳，杨日杰，熊华.非线性滤波方法在水下目标跟踪中的应用［J］.火力与指挥控制，2010(8):13-17.