传递对准中时间延迟误差补偿与滤波模型

吴训涛，高青伟

(1. 91550 部队，辽宁 大连 116023;2.海军航空工程学院 指挥系，山东 烟台 264001)

惯导系统传递对准中主要的误差源包括载体挠性误差、杆臂速度误差、数据传输延迟误差以及惯性元器件误差等［1］。由于传递对准卡尔曼滤波算法的实现是在子惯导系统中进行，这就需要将主惯导系统的一些相关信息(主要是速度和姿态信息)传输到子惯导系统，由于传输延迟的存在，导致传递对准误差。另外，对于平台式主惯导系统，传感器测量也需要一定的反应时间，从而导致测量信息的延迟。研究传输延迟的建模和补偿对提高惯导系统初始对准精度具有重要的意义。

卡尔曼滤波技术是对惯导系统进行传递对准最常用的一种有效方法。然而，为使卡尔曼滤波器具有最优性能，必须使卡尔曼滤波器模型和噪声统计特性具有准确的先验信息［2］。对于实际的惯导系统而言，往往存在着各种不确定性误差，若利用卡尔曼滤波器进行估计，导致滤波发散。

为解决这一问题，出现了许多自适应卡尔曼滤波算法，主要包括Sage-Husa 自适应滤波算法、模糊自适应卡尔曼滤波和衰减记忆卡尔曼滤波等。文献［3 -5］给出了衰减因子的自适应估计方法，具有一定的理论指导意义。本文提出了一种最佳自适应估计衰减因子的方法，可在线快速计算出衰减因子的估计值，将其应用于惯导系统的传递对准中，仿真结果优于传统的卡尔曼滤波。

1 传递对准数学模型

主子惯导系统误差方程建立所涉及到的坐标系关系如图1 所示。惯导系统传递对准流程如图2 所示，利用主子惯导的速度之差作为卡尔曼滤波器观测量之一;将主惯导的方向余弦矩阵和主惯导与标称机体坐标系的方向余弦矩阵送入到子惯导中，计算得到姿态误差作为卡尔曼滤波器另一个观测量，进行状态估计。

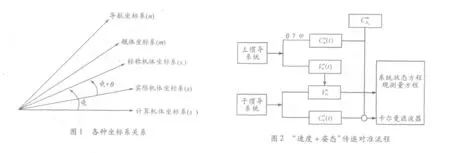
由于传递对准的时间很短，陀螺和加速度计所引起的相对速度、相对姿态误差很小，因此在建模时不考虑这些状态，而通过增加相对速度误差和姿态误差方程中的过程噪声，以补偿未建模的陀螺和加速度计测量误差［6］。

传递对准滤波器的状态变量可取为3 个相对速度误差δVx、δVy、δVz，3 个计算机体系^s 到标称机体系sv的相对姿态误差，即计算失准角φmx、φmy、φmz，3 个实际机体系s 到标称机体系sv的相对姿态误差，即物理失准角φax、φay、φaz。由于简化了动态模型，可增加过程噪声来补偿，将φa建模为˙φa=Wa，Wa是高斯白噪声。传递对准滤波器的数学模型可所示为:

2 考虑时间延迟的量测方程

设子惯导(SINS)在t 时刻获得主惯导(MINS)在t-Δt 时刻的数据信息，延迟时间对姿态的影响比较大，所以需要对姿态误差观测量进行相应的更新，当载体处于低动态时，延迟时间对速度观测量的影响可以忽略［6］。设主惯导在t -Δt 时刻的方向余弦矩阵为则有:

同理可得:

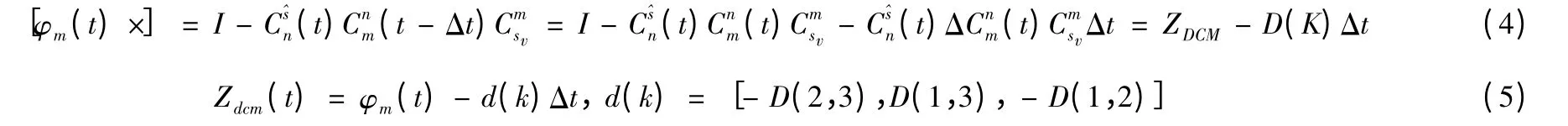
3 衰减记忆滤波器的最佳自适应算法

与常规卡尔曼滤波相比，衰减记忆卡尔曼滤波在一步预测误差方差阵计算式中增加了一个衰减因子，加重现时测量数据在状态估计中的作用，从而避免滤波器发散。通常衰减因子取为一个固定常数，在实际系统中，每一个误差状态估计程度是不一样的，用一个衰减因子不能确切修正所有误差状态估计异常的情况。而衰减记忆矩阵S(k)对每一个状态分别进行估计，从而保证衰减记忆滤波器工作在最佳状态。为使衰减记忆滤波器工作在最佳状态，应根据滤波器的最佳性条件在线自适应地调整衰减因子。

记估计残差为

最佳滤波在不同时刻的残差互不相关，用方程式表示为:

欲使Cj(k)≡0，(j≠0)，须满足:

式(9)构成了自动寻找最佳遗忘因子的基础。

最佳衰减因子的一步算法推导:

设系统满足条件①Q(k)，R(k)，P(0)均为正定对称阵;②输出矩阵H(k)行满秩。

把式(8)带入式(9)得:

由条件①、②及式(8)知，P(k|k-1)和C0(k)均为满秩对称阵，因而可在式(10)两边左乘P-1(k|k-1)及右乘C-10 (k)，整理有

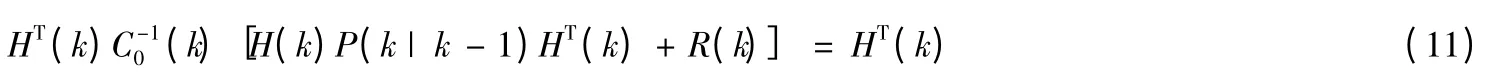
条件②已假设H(k)行满秩，式(11)隐含式(12)成立:

或

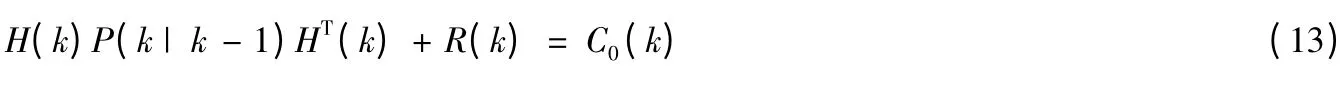
将 ( )S k 代入式(13):

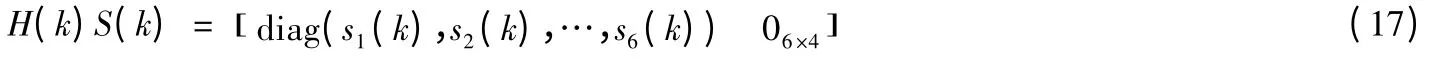
记mij(k)为M(k)的第i 行j 列的元素，记nij(k)为N(k)的第i 行j 列的元素，有

4 仿真试验

仿真条件及参数:子惯导陀螺常值漂移为0.05°/h，加速度计的零偏为5 ×105g，3 个安装误差角为60'，仿真时间设定为50 s，时间延迟误差为0.03 s。

初始状态估计值全取0，即

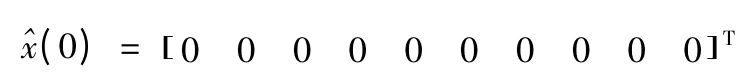
初始方差阵P0为对角阵，其中

量测噪声方差阵R 为对角阵，其中R(1，1)=R(2，2)=R(3，3)=(0.1 m/s)2，R(4，4)=R(5，5)=R(6，6)=(0.1°)2。

在P0=0.001P0，Q=0.01Q 条件下，分别用卡尔曼滤波和衰减记忆自适应滤波估计系统的状态，固定失准角估计曲线如图3 ～5 所示，图中的实线和虚线分别为采用衰减记忆自适应卡尔曼滤波和常规卡尔曼滤波时的失准角估计曲线，时间延迟误差估计曲线如图6 所示。2 种滤波算法下的固定失准角估计误差值如表1 所示，衰减记忆自适应滤波下的时间延迟估计误差为0.000 4 s。

表1 2 种滤波算法下固定失准角估计误差值

从仿真图形和数据可以看出，衰减记忆自适应滤波在考虑时间延迟和模型与噪声统计特性不确定性时估计固定失准角的估计精度和时间上优于常规卡尔曼滤波，水平失准角估计误差最大为0.9'，方位失准角误差为2'，时间延迟估计误差为0.000 4 s，满足惯导系统的传递对准的精度要求。

5 结论

针对传递对准中的时间延迟误差进行分析，建立时间延迟下的量测方程，并建立了衰减记忆自适应卡尔曼滤波模型，采用“速度+姿态”匹配算法进行了仿真试验，仿真结果表明，时间延迟误差会影响失准角的估计精度和时间，采用衰减记忆自适应卡尔曼滤波可以提高传递对准的精度和时间。

［1］扈光峰，王艳东，范跃祖.传递对准中测量延迟的补偿方法［J］.中国惯性技术学报，2005，13(1):10-15.

［2］付梦印，邓志红，张继伟.Kalman 滤波理论及其在导航系统中的应用［M］.北京:科学出版社，2003.

［3］徐景硕.自适应卡尔曼滤波器渐消因子选取方法研究［J］.系统工程与电子技术，2004，11(11).

［4］Xia Qijun，Rao Ming，Ying Yiqun，et al. Adaptive Fading Kalman Filter with an Application［J］.Automatica，1994，30(12).

［5］Levent Ozbek，Aliev Fazil.A Comment on Adaptive Fading Kalman Filter with an Application［J］.Automatica，1998，34(12).

［6］王力丹，张洪钺，戴汝为.一种快速传递对准的方法［J］.航天控制，2000(4):8-16.

［7］You-chol Lim，Joon Lyou. Transfer Alignment Error Compensator Design Using H∞Filter［J］.Proceddings of the American Control Conference Anchorage，2002(5):8-10.