弹道模型在旋转弹丸稳定性仿真中的应用

2012-07-02廖广辉

兵器装备工程学报 2012年5期

廖广辉

(徐州空军勤务学院武汉训练大队，武汉 430033)

弹丸飞行稳定性状况对弹丸飞行弹道有直接影响，是外弹道研究的重要内容。文献［1］分析了火炮射角和弹丸长径比对弹丸追随稳定性和动态稳定性的影响实质，得到其影响规律，该研究对弹丸设计具有重要参考价值。文献［2 -3］分别建立了脉冲力和脉冲力矩作用于弹道修正弹的弹道数学模型，对脉冲力和脉冲力矩影响下的弹丸稳定性条件进行了分析，其研究成果对弹道修正方案的选取具有参考意义。上述文献均建立了6 自由度的刚体弹道模型，却忽略了地球曲率的变化，对弹丸稳定性的分析精度有一定影响。

本文建立了高速旋转弹丸的质点弹道模型、修正质点弹道模型和刚体弹道模型，且在刚体弹道模型中考虑了地球表面曲率变化的影响，旨在分析和得到不同弹道模型在弹丸稳定性仿真中的优劣与规律。

1 弹道模型

1.1 质点弹道模型

质点弹道方程是实际弹道的最简单模型，一般作为研究实际弹道的基准。它是将弹丸作为质点处理，仅考虑重力和空气阻力的作用，忽略攻角的存在(即δ=0)，是3 自由度的弹丸运动微分方程。本文采用综合考虑自然风、地球表面曲率及重力加速度变化和科氏加速度影响的弹丸质点运动方程组，可参考文献［4］。

1.2 修正质点弹道模型

修正质点弹道模型是在质点弹道模型的基础上考虑了升力、马氏力和弹丸攻角引起的诱导阻力，提高了计算精度，是4 自由度的弹丸运动微分方程。修正质点弹道是空间曲线，相比于质点弹道更接近实际弹道。本文只列出其与质点弹道方程不同的部分［5］:

式中:bx为考虑攻角δ 影响的弹丸阻力系数;δx、δy、δz的直接算法可参考文献其他符号的物理意义可参考文献［6］。

1.3 刚体弹道模型

刚体弹道方程包括质心运动的动力学方程、绕心运动的动力学方程和质心运动学方程。本文基于坐标变换理论建立地球曲率影响下的刚体弹道模型。

地球曲率对刚体外弹道模型影响的物理本质是弹丸飞行过程中地面坐标系相对于地面固联坐标系有旋转角度φ［7］。考虑地球曲率时的坐标系如图1 所示。

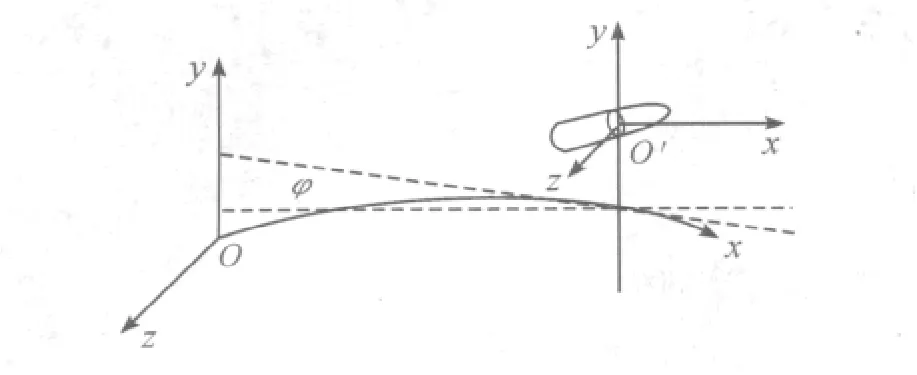
图1 考虑地球曲率时的坐标系

此时在弹丸质心运动的动力学方程中，弹丸加速度可分解为地面坐标系中的相对加速度和速度矢量v 随φ 变化的牵连加速度×v;弹丸绕心运动的动力学方程中，弹丸所受合力矩可分解为地面坐标系中的相对合力矩和动量矩矢量L随φ 变化的牵连力矩×L。

式中:∑Fix2、∑Fiy2、∑Fiz2为弹丸所受合力在速度坐标系各轴上的分量;∑Miξ、∑Miη、∑Miζ为弹丸所受合力矩在弹轴坐标系各轴上的分量;Bξ、Bη、Bζ和Cξ、Cη、Cζ分别为弹丸飞行t 时刻弹轴坐标系相对于地面坐标系转动的ω 以及角速度矢量˙φ 与弹丸所受动量矩矢量L 叉乘在弹轴坐标系各轴上的分量。

质心运动学方程反应弹丸飞行过程中相对地面固联坐标系的位置。考虑地球曲率的作用，只需考虑弹丸的飞行高度和地球半径将弹丸空中飞行速度向地面投影即可。

2 弹丸飞行稳定性计算

弹丸稳定飞行是指弹丸自发射至命中目标的全飞行过程中攻角δ 始终较小或逐渐减小。弹丸稳定性包括陀螺稳定性、追随稳定性和动态稳定性。

1)全弹道陀螺稳定性计算

在弹道上任意点的陀螺稳定因子

由4D 弹道模型或6D 弹道模型计算得到任意时刻的弹丸转速速度v、插值计算的kz，可根据式(4)计算出该时刻的陀螺稳定因子Sg。若每一时刻的Sg均大于1，则全弹道是陀螺稳定的。

2)全弹道追随稳定性计算

由4D 弹道模型或6D 弹道模型计算得到任意时刻的弹丸攻角δ。若δ 始终不大于动力平衡角的限定值［δp］，则弹丸的运动在全弹道上是追随稳定的。

3)全弹道动态稳定性的计算

在弹道上任意点的动态稳定因子

由4D 弹道模型或6D 弹道模型计算得到任意时刻的弹道倾角θ，弹丸速度v，插值计算的bx、by、ky、kzz，可根据式(5)计算出该时刻的动态稳定因子Sd。若每一时刻的Sd和Sg均满足SgSd(2 -Sd)＞1，则全弹道是动态稳定的。

3 案例仿真及分析

由得到的外弹道数学模型，利用四阶五级龙格- 库塔法，借助Matlab 软件编写计算程序，并对某口径榴弹的外弹道过程进行数值仿真。仿真输入数据如表1。仿真过程中用到的气动力和气动力矩系数由11 组试验数据经过一元三点不等距插值求得。

表1 仿真输入数据

为研究不同弹道模型在旋转弹丸外弹道性能仿真中的应用，分别利用质点弹道模型、修正质点弹道模型和刚体弹道模型对上述案例进行仿真，结果如表2 所示，弹丸攻角曲线如图2 所示，弹丸陀螺稳定性曲线如图3 所示，弹丸动态稳定性曲线如图4 所示。

表2 不同弹道模型的仿真结果

表2 中，3D、4D、6D 模型的仿真射程与实验射程10 575 m的相对误差［5］分别为0.96%、0.86%、0.60%，由此可知，描述旋转弹丸的数学模型越精确，其仿真结果越接近实验值。由弹丸空中飞行总时间tmax知，弹道模型中考虑的气动力和气动力矩越全面，弹丸空中飞行的时间越长，仿真射程越小，其仿真结果越精确。

图2 弹丸攻角曲线

由图2 知，在弹丸飞行的初始阶段，4D 模型不能较好地反映弹丸攻角的变化，这是因为弹丸出炮口时，弹道风是弹丸攻角产生和变化的主要原因，此时弹丸攻角姿态应是震荡的。在弹丸飞行的下降段，6D 模型求解的弹丸攻角值始终大于4D 模型，这是6D 模型仿真射程比4D 模型小的根本原因，因为弹丸攻角姿态愈差，其所受的气动力尤其是气动阻力越大，弹丸射程就愈小。由此可见，4D 模型虽采用了弹丸攻角的直接解法，却终因忽略次要气动力矩的作用而不如刚体弹道模型能够较好反映全弹道弹丸攻角的变化，从侧面验证了次要力矩对弹丸攻角的重要作用。由表2 知，4D 模型的仿真步长和质点模型一致，为0.1，远大于6D 模型的仿真步长，这使得4D 模型在解算中实时性较刚体弹道模型好，因此，4D 模型常用于火控系统中对来袭目标的实时解算，但需要一定的修正量。

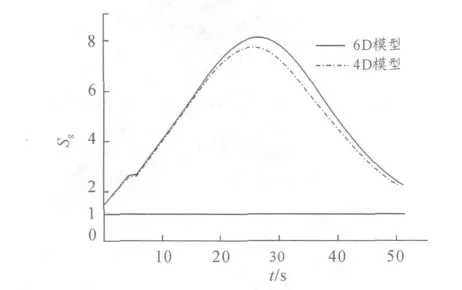
图3 弹丸陀螺稳定性曲线

由图3 知，旋转弹丸在全弹道上满足Sg＞1，能够较好满足陀螺稳定性的要求。由图4 知，在弹丸飞行的初始阶段，弹丸的动态稳定性较差，这是由于弹丸动态稳定性反映攻角的变化趋势。由图2 知此时弹丸攻角是震荡且有增加趋势的，因此不能满足弹丸动态稳定性要求。对比图2 ～4 知，在弹丸飞行的上升阶段，4D 模型和6D 模型对弹丸稳定性仿真结果的一致性较好，而在飞行的下降阶段一致性则较差。