永磁同步伺服系统全闭环建模及仿真

王景辉，乐贵高，霍 龙

(南京理工大学 机械工程学院，南京 210094)

永磁同步电机(PMSM)因其体积小、结构简单、输出转矩大、效率高等优点，在工业控制领域得到了广泛应用［1］。同时PMSM 是一个非线性、多变量、强耦合的时变系统，因此需要建立其解耦状态方程。1971年德国学者Blaschke 等［2］提出了矢量控制理论，使交流电机转矩和磁通的控制实现解耦。近年来电机控制中普遍采用SVPWM 技术，提高了逆变器的电压输出能力，并保持恒定的开关频率，特别适合数字控制。本文基于矢量控制的思想，采用电压空间矢量脉宽调制的方法对永磁同步电机伺服系统进行仿真分析。

1 永磁同步电机矢量控制

以转子为凸装式的永磁同步电动机为例［2］得到PMSM的电压电流、电磁转矩和机械运动方程为:

式中:id、iq为dq 轴电流;ud、uq为dq 轴电压;R 为定子电阻;L 为等效dq 轴电感;Pn为极对数;ψf为转子上的永磁体产生的磁势;ωr为转子机械角速度;J 为折算到电机轴上的总转动惯量;B 为粘滞摩擦系数;TL为折算到电机轴上的总负载转矩;Te为输出转矩。

从式(1)可以看出，ωr、id、iq是紧密耦合的。为实现交流电机的解耦控制，采用id=0 的矢量控制方式，则式(1)简化为:

当电机轴与减速器相连，且检测元件安装在被控对象即减速器输出轴上(减速器视为刚性)，组成全闭环系统，得到如下方程:

其中:θr为被控对象端角度输出;i 为减速比。

由以上推导可以得出PMSM 空间矢量控制框图如图1所示。

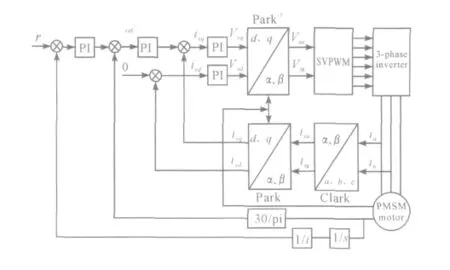
图1 永磁同步电机空间矢量控制方框图

2 永磁同步电机全闭环系统建模

在Matlab/Simulink 下建立各个模块仿真模型，步骤如下。

2.1 比例积分(PI)控制器

比例(P)控制的目的是快速调节系统偏差，积分(I)控制的目的是消除系统静差，在Matlab 中的模型见图2。

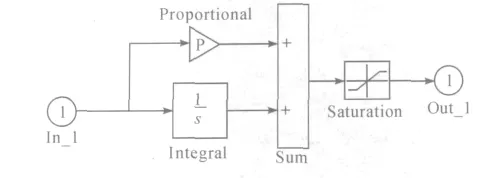
图2 PI 模型

2.2 坐标变换模块

坐标变换模块主要有从dq 旋转坐标系到两相静止αβ坐标系的Park-1变换，从两相静止αβ 坐标系到dq 旋转坐标系的Park 变换以及从三相静止ABC 坐标系到两相静止αβ坐标系的Clark 变换其表达式如式(4)～(6)所示。

2.3 SVPWM 模块和逆变模块

SVPWM 的实现算法在相关文献［3-5］中已有详述，本文不再赘述，其建立主要分为几个步骤:

1)确定空间电压矢量所在扇区

各扇区与Uα、Uβ的关系如式(7)所示:

图5 基本电压矢量作用时间模块

得到各扇区与N 的对应关系，模型如图3 所示。

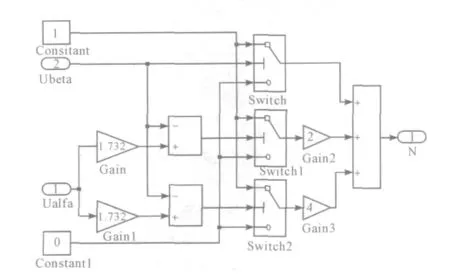
图3 扇区选择模块

2)X、Y、Z 的计算

两个相邻电压空间矢量在一个PWM 周期中的作用时间的公用公式X，Y，Z 的计算如式(7)所示，其模型见图4。

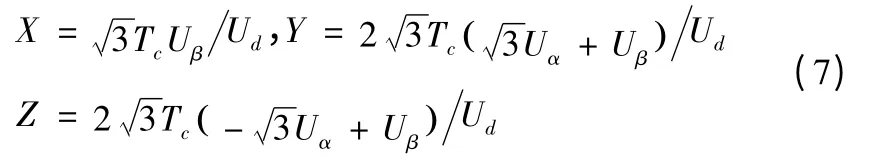
图4 X、Y、Z 计算模块

3)基本电压矢量作用时间模块

将两个相邻的非零电压空间矢量的作用时间表示为T1，T2，与X、Y、Z 的对应关系如表1。

表1 基本电压矢量作用时间计算公式

之后进行饱和判断，当T1+T2＞Tc时，

当T1+T2＜Tc时，T1，T2保持不变，

其模型如图5 所示。

4)Ta，Tb，Tc计算模块

Ta，Tb，Tc由下式确定:

模型如图6 所示。

5)PWM 波生成模块

计算得到的Tcm1，Tcm2，Tcm3值与周期为T，峰值为T/2 的三角波进行比较，可以生成对称空间矢量PWM 波形。将生成的PWM1，PWM3，PWM5 取反就可以生成PWM2，PWM4，PWM6。其模型如图7 所示。逆变器模块由Matlab 自带的模型生成，直流母线电压Udc 取230 V。

图6 Ta，Tb，Tc 计算模块

2.4 电机模型

永磁同步电机模型直接由Matlab 自带的模型生成，磁通选择正弦波模式。

2.5 检测模块

永检测模块也由Matlab 自带的模型生成，主要由三相电流、转子角速度、转子角度、输出转矩等组成。

由以上各模块得到完整的永磁同步电机三闭环控制系统仿真图如图8 所示。

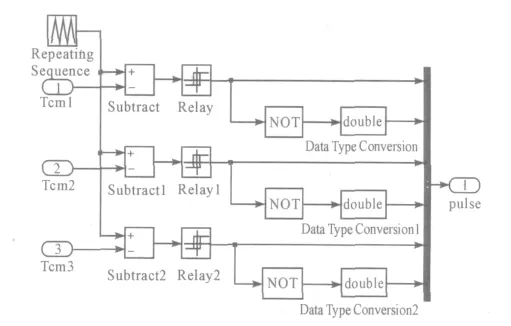
图7 PWM 波生成模块

图8 永磁同步电机空间矢量控制仿真模型

3 仿真结果

为了验证系统性能及所设计的仿真模型的正确性和有效性，进行了仿真实验。仿真参数:电机转动惯量J =2.627 ×10-3kg·m2，定子相电阻R =2.6 Ω，转子永磁体磁势Ψf=0.185Wb，等效电感L=5 ×10-3H，极对数pn=4，粘滞摩擦系数B=1.43 ×10-4N·m·s，减速器减速比为1∶192。

3.1 速度仿真

仿真条件为电机空载启动，转速给定为300 r/min，在t=0.04 s 时突加负载转矩6 N·m。电机的转速、转矩曲线以及定子三相电流如图9 ～11 所示。

从图中可以看出，电机在空载启动时电流、电磁转矩迅速达到最大值，然后稳定在正常值;在0.04 s 突加负载转矩时，电流、电磁转矩经过一个轻微的振动过程后分别稳定在一个新值。转子角速度迅速稳定到给定转速，存在一定的超调，突加负载时转速有所降低，但能迅速恢复到额定状态，稳态运行时无静差。

3.2 位置仿真

仿真条件为电机空载启动，位置给定为10°，在t =0.5 s时突加负载转矩10 N·m。位置及转矩输出曲线如图12 ～13 所示。

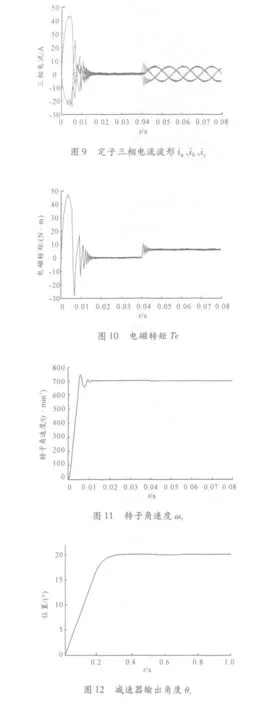
图13 电磁转矩Te

从图中可以看出，位置响应快速、无超调，突加负载时位置曲线几乎不受影响，稳态运行无静差;电磁转矩在电机启动和突加负载转矩时有明显振荡，但能在很短的时间稳定在常值，且此时的位置及转矩曲线已非常稳定平滑。

4 结束语

本文在分析永磁同步电机矢量控制模型的基础上，在Matlab/Simulink 环境下建立了基于空间矢量脉宽调制控制的永磁同步电机三闭环伺服系统，采用PI 控制策略设计了系统的电流、速度及位置调节器，易于工业控制的实现。仿真结果表明，系统能平稳运行，具有良好的速度响应及位置跟踪特性，同时为实际电机控制系统的设计及控制研究提供了有效地手段和工具。

［1］Jianguo Zhoua，Youyi Wang. Real time nonlinear adaptive backstepping speed control for a PM synchronous motor［J］.Control Engineering Practice，2005(13):1259-1269.

［2］舒志兵.交流伺服运动控制系统［M］.北京:清华大学出版社，2006.

［3］姚绪梁.现代交流调速技术［M］.哈尔滨:哈尔滨工程大学出版社，2009.

［4］程晓猛，陆海峰.用于逆变器死区补偿的空间矢量脉宽调制策略［J］.清华大学学报:自然科学版，2008，48(7):1077-1080.

［5］沈艳霞，吴定会.永磁同步电机位置跟踪控制器及Backstepping 方法建模［J］.系统仿真学报，2005，17(6):1318-1325.

［6］张森，石航飞，陈志锦，等.基于DSP 的永磁同步电机的矢量控制［J］.兵工自动化，2011(10):71-74.