本振相位噪声对接收机性能的影响✴

李永波

（中国西南电子技术研究所，成都610036）

本振相位噪声对接收机性能的影响✴

李永波

（中国西南电子技术研究所，成都610036）

针对工程中本振相位噪声对接收机的影响常难以估量的问题，提出利用等效相位白噪声谱密度进行评估的方法。通过分析相位噪声的产生及其对剩余误码率和动态范围的影响机理，仿真了不同相位噪声对误码率的影响程度。通过仿真结果可知：相位噪声对接收机性能具有重要的影响，工程中应针对不同的应用场合要求合理的相位噪声指标。

超外差接收机；相位噪声；本振；剩余误码率；动态范围

1 引言

本振是超外差式接收机的核心部件之一，其相位噪声将通过频率变换使得接收信号产生畸变，这种畸变将对接收机产生重要的影响。对本振相位噪声指标的不同需求，将影响本振单元甚至整个接收系统的实现形式和难易程度［1］。

已有文献通常采用将单边带相位噪声转换为相位抖动均方值，再通过将相位抖动均方值与误码率进行仿真的方法得出相位噪声对系统误码率的影响［1-2］，然而，相位抖动均方值与接收系统的信噪比难以有直观联系。因此，本文从另一个角度，采用等效相位白噪声谱密度的方法进行分析。本文首先介绍了相位噪声的概念，分析了因其所带来的剩余误码率产生机理，及其对接收机动态范围的影响机理，在接收系统的仿真分析中引入等效相位白噪声谱密度的概念，通过对同一系统采用多组不同的相位噪声进行仿真，直观地反映了相位噪声对接收机的影响。该方法可以直观地反映相位噪声与接收机误码率的关系，为系统分配合理的相位噪声提供了一种新思路。

2 相位噪声的概念

不考虑初始相位，一个理想的本振输出信号可以表示为式中，V（t）为信号瞬时电压，V0为信号标称峰值电压幅度，f0为信号标称频率，其中V0、f0均为常数。这是一个纯净的本振信号，从频域看本振信号为一根纯净谱线，从时域看正弦波的周期为一恒定值。但实际中任何信号不可避免地被噪声调制。

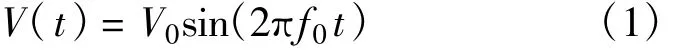
实际本振可表示为

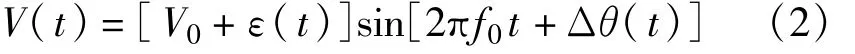
式中，ε（t）为瞬时幅度起伏，Δθ（t）为各种原因造成的附加瞬时相位起伏。其中ε（t）和Δθ（t）均为随机过程，通常情况下ε（t）≪V0，即在接近f0的偏移频率上，由随机幅度变化引起的噪声功率远远小于由随机相位变化引起的噪声功率［3］。此外，接收机混频器通常工作于本振输入功率饱和的状态，这会减小其对本振幅度变化的敏感程度。因此，忽略幅度起伏，本振中的所有噪声可看作是由相位起伏Δθ（t）引起的。式（2）可以简化为

其中：

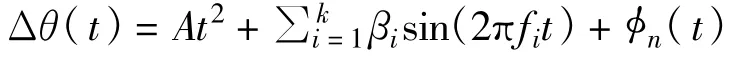
式中，第一项为系统频率的线性漂移；第二项为周期性杂散信号的调制，βi和fi分别为杂散信号的调制度和频率；第三项φn（t）是相位的随机起伏，即相位噪声。

在实际的分析中，频率线性漂移是一个慢速变化量，对瞬时相位变化影响较小，可以忽略；杂散只要控制在一定范围内，如低于载波50 dB，其对相位的动态变化也可不考虑。因此，可以将式（3）简化为V（t）=V0sin［2πf0t+φn（t）］

假设载波频率为f0且静止，与本振频率f0间隔fm处，1 Hz带宽内的噪声电压在时间小于1／B s（B为射频带宽）时，可以认为该噪声电压是一频率为f0+Δf的正弦波。用矢量相量法可以计算出载波电压和噪声电压两个不同频率的正弦波矢量相加的结果。噪声电压的旋转角速度为Δω=2πΔf。

3 剩余误码率的概念

为了降低系统误码率，通常想到的方法是提高接收信号的电平，即增加接收信号的信噪比。在接收门限附近这种措施是非常明显的，但当信噪比继续增加到一定程度时，误码率几乎不再变化，而是停留在一个固定值附近，这就是剩余误码率［4］。

由图1仿真可见，在接收门限附近，随着信噪比的增加误码率迅速降低。这是因为，在这一区间引起误码的主要因素是系统的随机热噪声。当接收信噪比进一步增加到一定程度时，误码率不再随着接收信噪比的增加而降低，此时进入误码不归零区域，即剩余误码率区域。在这一区域中，由系统本振源所引入的相位噪声是造成误码的主要因素。度为2V0，噪声正弦波幅度为2N0。

相位噪声属于一种平稳随机过程，可用频域中的噪声功率谱密度进行表示，通常采用频率起伏谱密度、相位起伏谱密度、相对频率起伏谱密度和单边带相位噪声表示，以上几种表示是针对不同应用场合提出的表征本振短期频率稳定度的参数，本质上它们是等效且可以相互转换的。由于相位噪声在频域上呈对称分布，工程中通常采用单边带相位噪声L（fm）表示（其单位为rad2／Hz，dB数为dBc／Hz），表示在偏离载波fm处1 Hz带宽内的相位调制边带噪声功率与载波功率的比值。

图1 64QAM误码率与信噪比关系图Fig.1 Relationship between BER and SNR about64QAM

以64QAM调制系统为例，图2中（a）是由随机热噪声所引起的误码示意图，（b）是由本振相位噪声所引起的剩余误码示意图。由此可见，对于高阶QAM调制系统，由本振相位噪声所引起的星座图旋转将给系统解调带来剩余误码率。

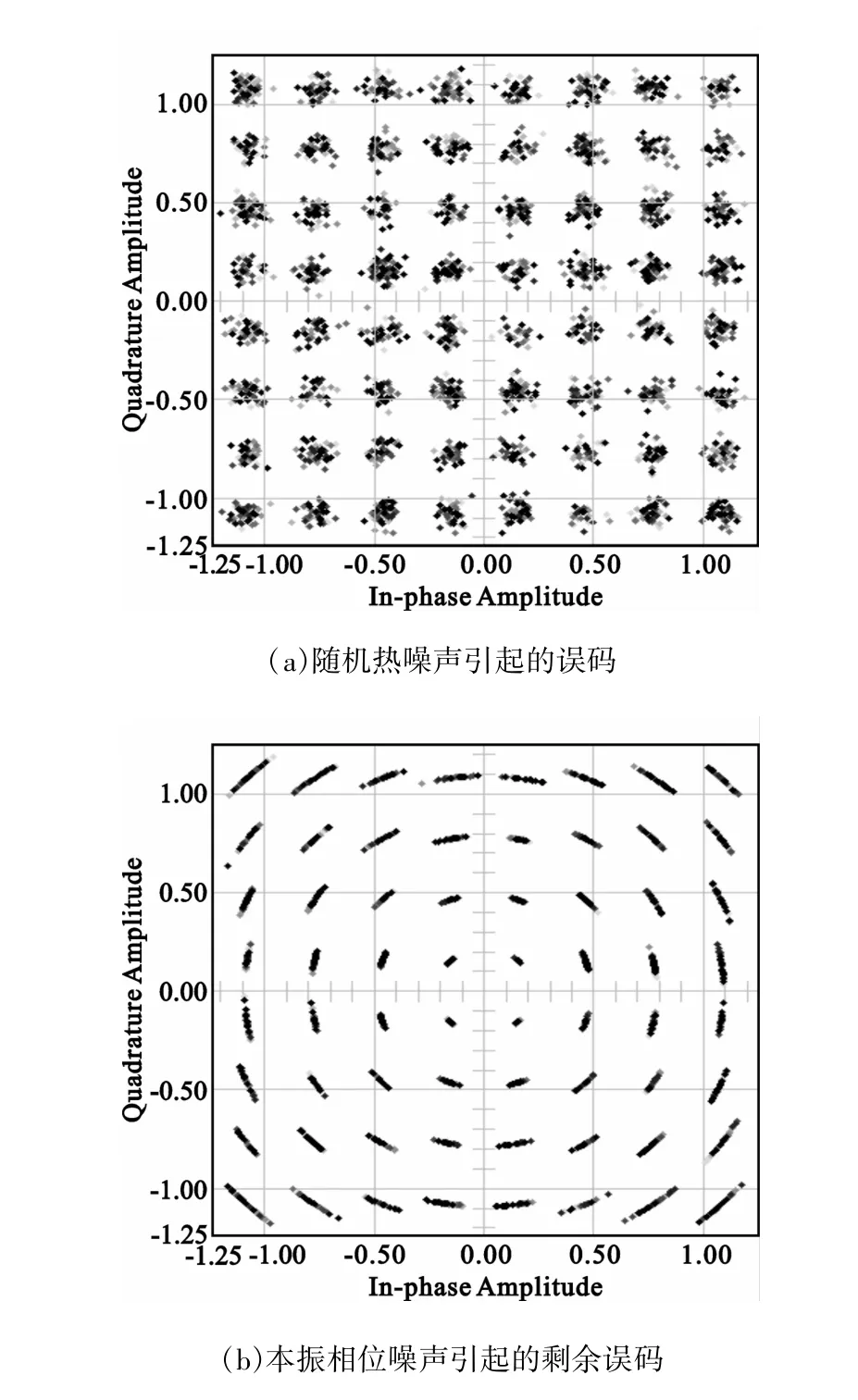
图2 误码特性示意图Fig.2 The demonstration diagram of biterror

4 相位噪声对动态范围的影响

为了适应现代电磁频谱的特点，对接收机提出了各种更高的要求，如高灵敏度、大动态范围和良好的选择性等。尤其是在通信、雷达一体化电子侦察中，要求接收机能处理同时进入接收机的强、弱信号，这就对本振的相位噪声提出了严苛的要求。如图3所示，在弱信号的相邻通道处存在强干扰信号，这两种强度不同的信号同时进入混频器，当本振噪声差时，就有可能导致弱信号在中频输出时被干扰信号的噪声边带所淹没，即产生所谓“倒易混频”现象。如果本振相位噪声好，则在中频输出端仍然可以分辨出混频后的弱信号。

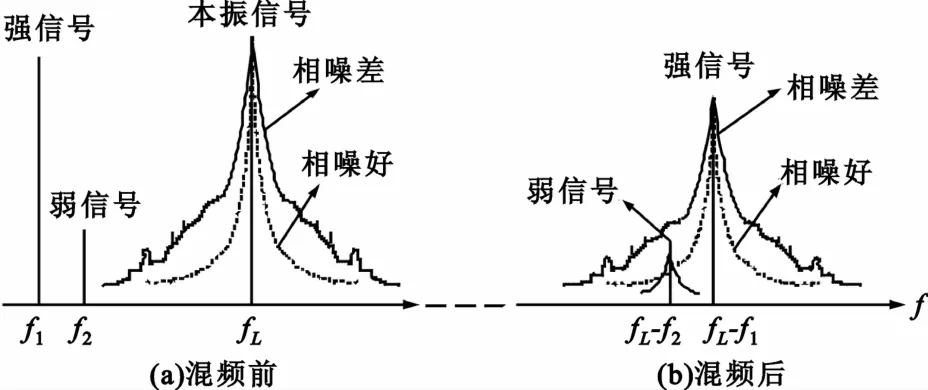
图3 相位噪声对动态范围的影响Fig.3 The effect of phase noise on dynamic range

从接收机动态范围的角度考虑，对本振的相位噪声的要求为：在系统要求的最小分辨率处，本振单边带相位噪声应优于系统的接收机动态范围，并适当留有一定余量。例如，接收系统要求的最小分辨率为10 kHz、动态范围为60 dB，那么，本振的单边带相位噪声在10 kHz至少要达到65 dBc。除此之外，考虑弱信号参数测量、解调时所需信噪比等因素，在10 kHz处的单边带相位噪声要远优于65 dBc，理想情况是对弱信号的载噪比不产生恶化。

5 相位噪声对误码率的影响

在数字通信系统中，决定系统误码率的主要因素是解调时的信噪比，当本振的相位噪声差时，本振的引入将影响解调信号的信噪比。相位噪声属于平稳随机过程，且其统计均值可以认为是零，因此，其均方值与方差等价。根据中心极限定理，电子系统中的热噪声及相关噪声具有零均值正态分布的平稳随机过程，所以相位噪声的相位变化分布可以表示为

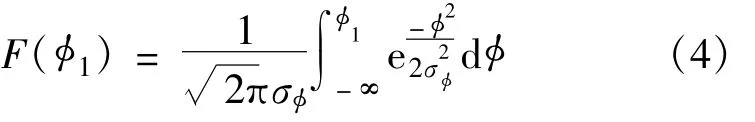
本振的相位噪声可以用一个等效近似的相位白噪声来代替［5］，其替代条件是：

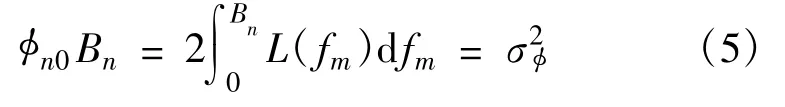
式中，φn0为等效的相位白噪声谱密度，Bn为接收系统的等效基带噪声带宽。图4可以直观地表示等效相位白噪声谱密度的原理，当图中A、B两部分的面积相等时，即可求得φn0。

图4 相位白噪声等效面积法Fig.4 Equivalent area of phase white noise

载波相位噪声在偏离载波零频到无穷大上都有分布，而在载波附近的相位噪声最为显著。因此，由图4可知，对于低数据率通信，等效的相位白噪声谱密度较大，所以低数据率对本振的相位噪声要求更高。

如前所述，由于相位抖动σφ的存在将引起接收信号的矢量波动，导致解调信号信噪比的恶化，影响接收系统的误码率。特别是对于频谱利用效率较高的高阶QAM调制，较差的本振相位噪声将严重影响系统的解调误码率。图5为256QAM调制、载波频率偏移2 kHz情况下，采用不同的等效相位白噪声谱密度对同一接收系统解调误码率的仿真结果。

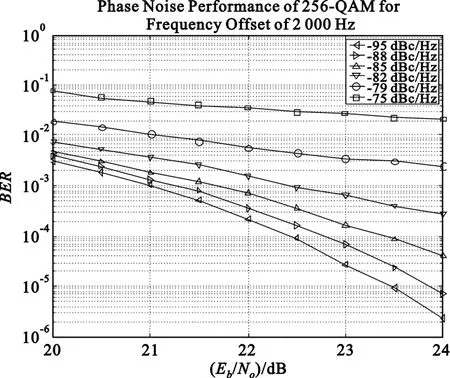
图5 相位噪声对误码率的影响Fig.5 The effectof phase noise on BER

由图中曲线的分布可知：以同一信噪比情况下，在本振等效相位白噪声谱密度较差时，随着相位噪声的改善，接收系统的误码率改善较为明显；在本振等效相位白噪声谱密度较好时，再进一步降低相位噪声，接收系统的误码率改善不再明显。这说明降低本振的相位噪声，即提高本振的频谱纯度有利于系统误码率的改善，但是当系统误码率达到一定程度时，再一味地过分追求高频谱纯度的本振并不能显著提高系统误码性能，反而会使得本振的实现方式异常复杂，成本变得昂贵甚至不可实现。从解调误码率的角度考虑，当本振的等效相位白噪声谱密度低于接收信号的C／N0一个量级时，相位噪声所带来的影响便可忽略不计。

6 结论

本振相位噪声是超外差接收机无法回避的一种噪声源，本文在接收机的分析及仿真中引入等效相位白噪声谱密度的概念，从另一个角度研究了相位噪声对接收性能的影响。仿真结果表明相位噪声对接收机性能具有重要的影响，工程中针对不同的场合，应要求合理的相位噪声指标。本文等效相位白噪声谱密度的分析角度，为系统对本振相位噪声进行合理的指标分配提供了另一种思路。

［1］Grebenkemper C J.本振相位噪声及其对接收机性能的影响［J］.和新阳，雷颖蓓，译.空间电子技术，2003（1）：4-13. Grebenkemper C J.Local Oscillator Phase Noise and Its Effect on Receiver Performance［J］.Translated by HE Xinyang，LEIYing-bei.Space Electronic Technology，2003（1）：4-13.（in Chinese）

［2］Mody A N，Shadaram M.Performance of QAM fiber optic links under the influence of RF phase noise［C］／／Proceedings of1998 International Conference on Applications of Photonic Technology.Toronto：SPIE，1998：527-531.

［3］Vaccaro D D.电子战接收系统［M］.付大毛，胡永福，译.北京：总参谋部第四部，1996：116-117. Vaccaro D D.Electronic Warfare Receiving System［M］. Translated by FU Da-mao，HU Yong-fu.Beijing：The Fourth Department of the General Staff Headquarters，1996：116-117.（in Chinese）

［4］陈大龙.相位噪声对QAM数字微波通信系统误码率的影响［D］.长沙：国防科技大学，2004. CHEN Da-long.The Effects of Phase Noise on BER of QAM Digital Microwave Communication System［D］.Changsha：National University of Defense Technology，2004.（in Chinese）

［5］刘嘉兴.相位噪声对数传误码率的影响［J］.电讯技术，2007，47（4）：63-65. LIU Jia-xing.The Effect of Phase Noise on BER of Data Transmission［J］.Telecommunication Engineering，2007，47（4）：63-65.（in Chinese）

Effect of Local Oscillator Phase Noise on Receiver Performance

LIYong-bo
（Southwest China Institute of Electronic Technology，Chengdu 610036，China）

To solve the problem that the effect of local oscillator phase noise on the receiver performance is immeasurable in practice，themethod of using equivalentwhite noise to evaluate the effect is proposed.Through analysing the generation of phase noise，and the affectionmechanism of residual BER and dynamic range，the influence degrees of differentphase noises on BER are simulated.The simulation results show thatphase noise is important to the performance of receiver.For different applications，the reasonable phase noise should be required.

superheterodyne receiver；phase noise；local oscillator；residual BER；dynamic range

the M.S.degree from Chongqing University in 2007. He is now an engineer.His research concernswideband receiver and satellite payload.

1001-893X（2012）04-0562-04

2011-12-20；

2012-03-30

TN911.4

A

10.3969／j.issn.1001-893x.2012.04.028

李永波（1981—），男，四川雅安人，2007年于重庆大学获工学硕士学位，现为工程师，主要研究方向为宽带接收机及卫星有效载荷。

Email：liyongbo8848＠126.com

LIYong-bo was born in Ya′an，Sichuan Province，in 1981. He