数字调制信号制式识别新方法✴
2012-07-01周敏冯全源
周敏,冯全源
(西南交通大学微电子研究所,成都610031)
数字调制信号制式识别新方法✴
周敏,冯全源
(西南交通大学微电子研究所,成都610031)
通过分析数字调制信号功率谱及高阶谱特征,对高阶谱的求取方法作了改进,并在此基础上提出新的特征参数,结合瞬时统计特征,采用支持向量机分类器,实现了AWGN信道下数字通信信号的制式自动识别。仿真表明,所提取的特征参数具有较好的抗噪性能,对调制参数的变化具有稳健性。考虑脉冲成形的影响,在信噪比大于12 dB时,单种信号最低正确识别率大于98.5%,平均识别率达99.5%以上。
调制方式识别;谱分析;特征参数提取;支持向量机;脉冲成形
1 引言
通信信号的调制方式自动识别是位于信号接收和解调的中间过程,为接收机选择正确的解调算法提供重要依据。在过去的20年间,自动调制识别一直是情报拦截和电子对抗等军事领域的重要研究课题。近年来,随着软件无线电(Software Radio, SR)[1-2]和认知无线电(Cognitive Radio,CR)[2]的高速发展,自动调制识别技术在民用领域的作用也愈显重要。
目前的调制识别算法可以分为判决理论识别方法和统计模式识别方法。判决论方法可以在低信噪比下得到较高的识别率,但其需要一些先验知识并且计算复杂[3]。统计模式识别法先从原始数据中提取有用的特征参数,然后通过某种分类器来确定未知信号的调制方式。这种方法不需要接收信号的先验知识,识别范围广,适用于信号的盲识别。根据特征提取方法的不同,现有的统计模式识别大概又可以分为基于时域特征[4-5]的提取方法和基于变换域[6-9]的提取方法。时域特征主要包括信号的瞬时幅度、瞬时频率和瞬时相位,这种方法以A.K.Nandi[4-5]等人的研究工作最具代表性。该方法易受噪声影响,在低信噪比下识别率不高。变换域方法主要包括时频域分析法[6]、高累积量分析法[7]、循环谱特征分析法[8]以及谱分析法[9-10]等。文献[6]采用小波变换提取特征参数,该方法对伸缩尺度这一参数并没有给出明确的选取规则,选取不好甚至会导致算法失效。文献[7]用高阶累积量的方法对MPSK信号进行了分类识别,但该方法对频偏敏感。文献[9-10]基于功率谱以及高次谱特征,提出一些抗噪性能良好的特征参数,但为了处理方便,这些高次谱需要先进行高通滤波处理,高通滤波器的系数不好设置,可操作性不强。
本文在前人研究的基础上提出基于功率谱和改进高阶谱的4个特征参数。根据这些识别特征,结合支持向量机分类器,提出一种数字通信信号识别的新方法。本文提出的识别算法简单,易于实现,抗噪性能良好,能对较大带宽内的调制信号进行正确识别,并且考虑了脉冲成形,适合工程应用。
2 问题假设与算法设计
本文所处理的通信信号调制识别是在前端接收机已经完成信号分离、下变频等预处理的基础上完成的。信号传输信道为加性高斯白噪声(AWGN)信道。根据分类算法的特点,本文采用统计模式识别方法,分为特征参数提取和调制方式识别两个步骤,如图1所示。

图1 统计模式识别方法流程Fig.1 Process of statistical pattern recognition
2.1 数字调制信号特征参数提取
对于已经完成信号分离和下变频处理的中频信号,先进行零中心包络归一化处理,主要是为了减小噪声、信道衰落以及成形滤波对信号幅度包络带来的影响。针对待识别的数字调制信号特点,本文提取信号的以下5个特征参数。
(1)倍频带宽比Λb
倍频带宽比定义为倍频信号和原信号的带宽之比,定义式为

式中,wd2为倍频信号的带宽,wd1为原始接收信号的带宽。倍频信号定义为同相信号和正交信号之积,为传统高阶谱的一种改进方法。该参数用于区分调制信息携带在瞬时频率上的MFSK/MSK信号和调制信息不携带在频率上的ASK/MPSK信号。
对于MFSK/MSK信号,倍频处理后调制指数加倍,其带宽近似变为原信号的2倍,因此MFSK/MSK信号的倍频带宽比约为2。而BPSK信号倍频后成为一个2倍中心频率的连续波(CW)信号,带宽接近于0,因此BPSK信号的Λb接近于0。另外,QPSK和8PSK信号在倍频处理后分别成为载频为2倍原信号载频的BPSK和QPSK信号,根据MPSK信号的带宽计算公式,其Λb约等于1。最后,对于调制信息携带在瞬时幅度上的ASK信号,倍频后中心频率搬移到2倍原载波频率处,带宽不变,因此ASK信号的Λb也约为1。综上所述,通过该参数也可以将待识别的7种数字信号分为{MFSK、MSK}和{MPSK、ASK}两个子集。另外,该参数也可以将{BPSK}和{ASK、QPSK、8PSK}区分开来。
事实上,利用信号的I/Q路而不直接对信号平方得到倍频信号的好处是可以避免直流项的产生,从而可以省掉去除直流分量的滤波器。在通信系统中,前端接收机往往已经将接收信号分解为I/Q路再送入信号系统中,因此在此不需要对信号进行Hilbert变换。
(2)零中心非微弱信号段归一化瞬时频率绝对值的标准差δaf[5]
该参数定义如下:
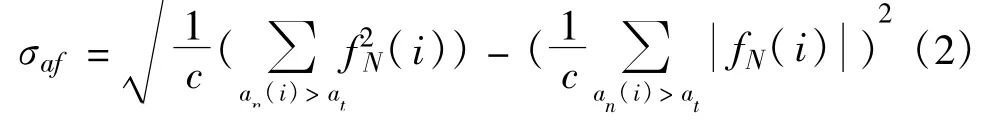
式中,fN为零中心非微弱段归一化瞬时频率序列,c为非微弱信号段样本点数。该参数用于区分包含绝对频率信息的2FSK和包含绝对频率的4FSK信号。
(3)归一化功率谱谱峰度Pk
归一化频谱峰度的定义式如式(3)所示:
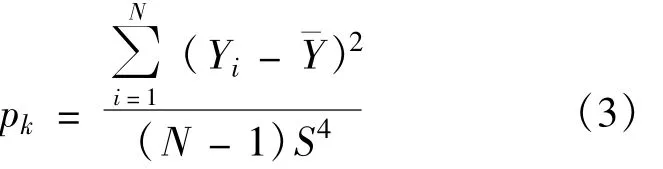
式中,¯Y为信号归一化功率谱的均值,S是归一化频谱的标准差N是数据段样本点数。该参数描述了分布形态的陡缓程度,用来度量数据在中心聚集程度,用于区分频谱高度集中的ASK信号和频谱相对分散的MPSK(M=4,8)信号。
(4)四倍频信号功率谱最大值Γmax
该参数定义为四倍频信号功率谱谱峰的最大值,用于区分QPSK信号和8PSK信号。这里的四倍频信号是经过信号两次同相和正交相信号相乘的结果,即先对接收到信号的I路和Q路信号做乘运算得到一个乘积信号x(t),然后对x(t)做希尔伯特变换得到其正交项y(t),最后求x(t)和y(t)的乘积得到四倍频信号。这样得到四倍频信号的好处是可以避免四次方运算产生的其他不需要的频率分量,为传统四阶信号的一种改进方法。QPSK信号四倍频后为中心频率为原值四倍的CW信号,其频谱表现为单根谱线,而8PSK信号四倍频后还包含相位跳变余量,其频谱表现为以四倍载频为中心的梳状谱。由于信号在接收送入信号处理系统先进行了包络归一化处理,因此信号的总能量值相等。综上所述,QPSK信号的Γmax比8PSK信号的Γmax大。
(5)归一化功率谱带内谱线密度、能量密度积Πs
该参数定义为信号归一化功率谱带内谱线密度和能量密度之积,用于区分2FSK和MSK信号,其定义式如式(4)所示:

其中,B表示信号归一化功率谱幅值大于特定门限值at的粗估计带宽,n表示带宽内大于at的谱线条数,∑ai表示带宽内大于at的谱线幅值之和。
由于MSK信号的频谱表现为以两个载频为中心的梳状谱,其载频受到抑制,而2FSK信号的频谱有两个谱峰。因此对信号功率谱进行归一化处理后,MSK信号的Πs参数较2FSK信号大,利用该参数可以对2FSK信号和MSK信号进行分类。
2.2 支持向量机分类器与识别流程
支持向量机(Support Vector Machine,SVM)的核心思想是通过非线性变换将一个线性不可分的低维空间映射到一个线性可分的高维空间,在高维空间以结构风险最小为原则构造最优分类超平面。它在解决小样本、非线性以及高维模式识别中表现出了特有的优势。与决策树分类器相比,支持向量机不需要设置特定的门限值。与神经网络分类器相比,支持向量机可以避免过学习或欠学习的问题。除此之外,支持向量机在训练样本较少的情况下仍然能够取得较好的识别结果。本文采用支持向量机对接收的未知调制模式信号进行识别。
结合提取到的每个特征采用二叉树结构分类器对信号进行分类,这种分类器的特点是判断逻辑简单,支持向量机数量较少,训练样本依次递减。本文算法SVM分类器结构如图2所示。
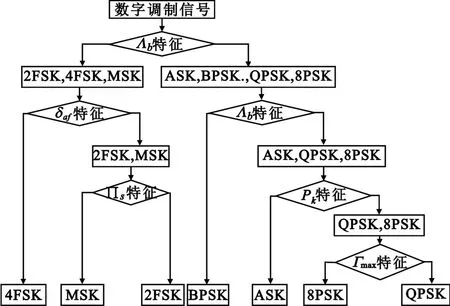
图2 数字调制信号分类器结构Fig.2 Structure of classifier for digitalmodulated signals
3 仿真结果与结论
3.1 仿真条件
所有仿真是在MATLAB7.9.0平台上进行的。信号源采用随机二进制序列,采样率为128 MHz,载波频率为11.3 MHz,符号速率为3.5 MHz,每次对2 048个样本点进行处理,成形滤波器采用升余弦滚降函数,滚降系数为0.4,噪声为加性高斯白噪声。
3.2 特征参数随信噪比变化仿真结果
为了测试本文提出的特征参数的抗噪性能,在不同信噪比条件下对这些特征参数进行仿真。设信噪比为从5~30 dB以1 dB为间隔变化,各特征参数仿真结果如图3所示。
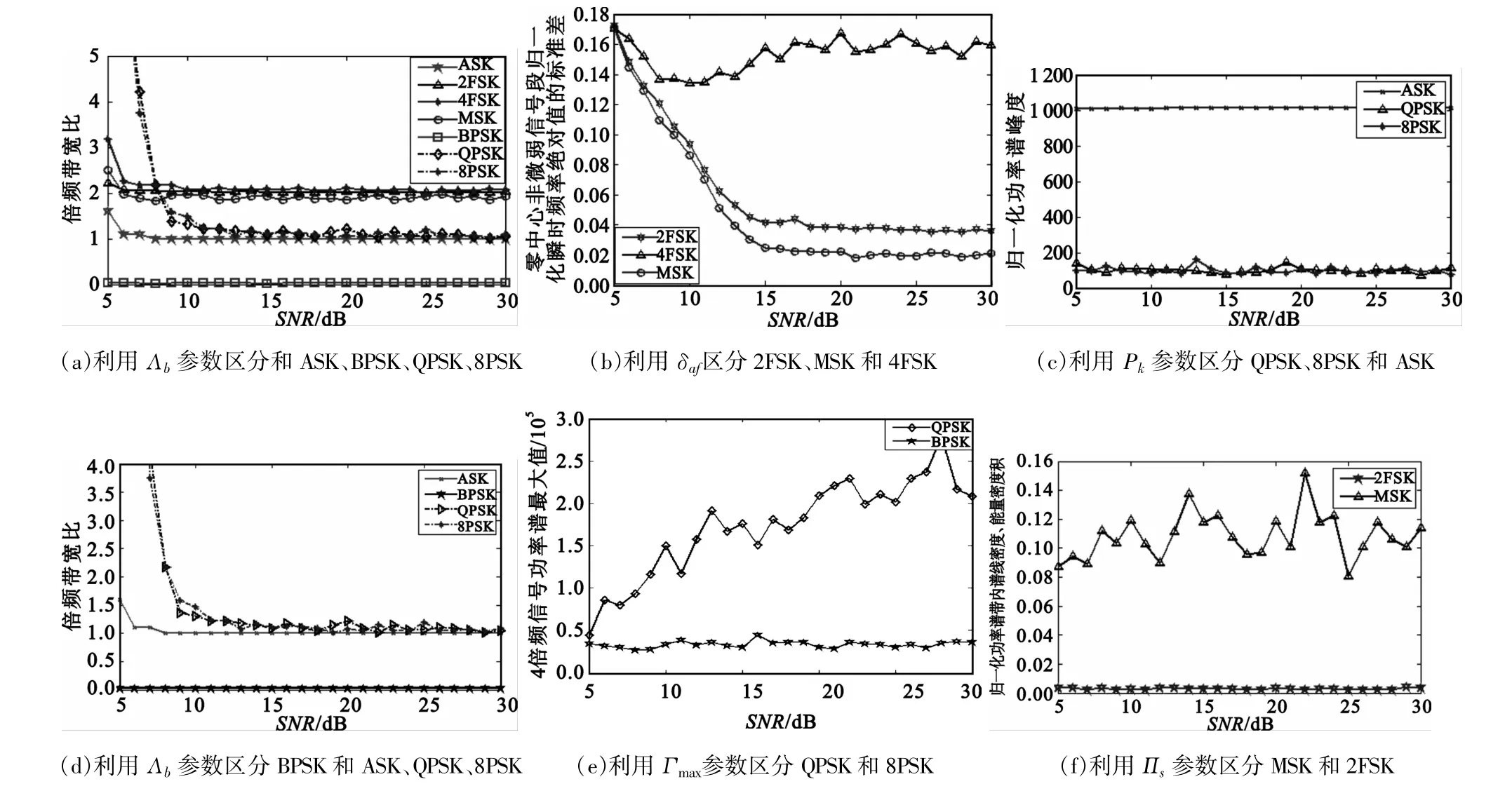
图3 各个特征参数随噪声的变化趋势Fig.3 Values of each feature parameter against SNR
3.3 特征参数随符号速率变化仿真结果
为测试本文算法对符号速率的敏感度,在其他仿真条件不变的情况下对符号速率进行3~10 MHz以1 MHz为间隔进行扫描,MFSK信号频偏等于符号速率值,信噪比为20 dB,每种测试条件下进行50次独立仿真,测试结果如图4所示。

图4 各个特征参数随符号速率年的变化趋势Fig.4 Values of each feature parameter against symbol rate
从图4可以看出,本文提出算法所采用的特征参数对符号速率在3~10 MHz变化时不敏感,说明本文算法能够在较大带宽内完成识别。
3.4 支持向量机分类识别仿真
为验证本文算法的性能,结合支持向量机,在信噪比为12 dB时用本文算法对每种调制信号进行500次独立仿真,识别正确率如表1所示。
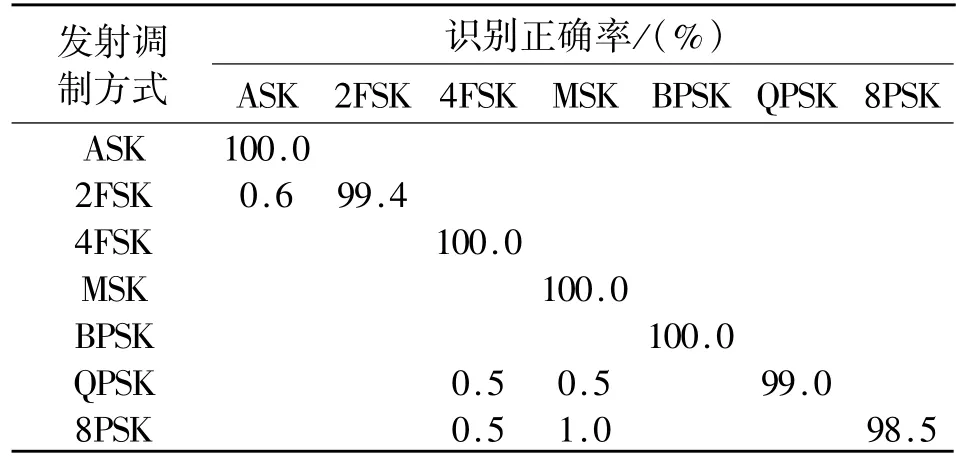
表1 在12 dB情况下本算法识别准确率测试结果Table 1 Simulation results of successful recognition rate at12 dB SNR
图5显示了信噪比从4~20 dB以2 dB为间隔变化时本文算法的正确识别率,每次测试时每种信号随机产生500个样本进行独立识别仿真,识别结果如图5所示。

图5 不同信噪比下的正确识别率Fig.5 Correct recognition rate at different SNR value
由于本文采用的带宽估计方法容易受噪声影响,导致倍频带宽比这个特征参数在低信噪比条件下分类效果不理想,因而研究受噪声影响小的带宽估计方法将是本文将来研究工作的一个重点。除此之外,更加复杂环境下的信号制式识别也是需要深入研究的问题。
[1]Mitola J.The software radio architecture[J].IEEE Communications Magazine,1995,33(5):26-38.
[2]陶玉柱,胡建旺,崔佩璋.软件无线电技术综述[J].通信技术,2011,44(1):37-39. TAO Yu-zhu,HU Jian-wang,CUI Pei-zhang.An Overview of Software Radio[J].Communications Technology,2011,44(1):37-39.(in Chinese)
[3]Hameed F,Dobre O,Popescu D.On the likelihood-based approach to modulation classification[J].IEEE Transactions onWireless Communications,2009,8(12):5884-5892.
[4]Nandi A K,Azzouz E E.Modulation recognition using artificial neural networks[J].Signal Processing,1997,56(2):165-175.
[5]Nandi A K,Azzouz EE.Algorithms for automaticmodulation recognition of communication signals[J].IEEE Transactions on Communications,1998,46(4):431-436.
[6]薛磊,刘小秋.基于小波变换的数字通信信号识别[J].电讯技术,2006,46(3):52-56. XUE Lei,LIU Xiao-qiu.Modulation Identification of Digital Signals[J].Telecommunications Engineering,2006,46(3):52-56.(in Chinese)
[7]陆凤波,黄知涛,易辉荣,等.一种基于高阶累积量的数字调相信号识别方法[J].系统工程与电子技术,2008,30(9):1611-1615. LU Feng-bo,HUANG Zhi-tao,YIHui-rong,et al. Recognition algorithm of phase shift keying signals by higher -order cumulants[J].Systems Engineering and Electronics,2008,30(9):1611-1615.(in Chinese)
[8]王瑛,程汉文,吴乐南.基于谱相关特征的信号调制方式识别[J].信息技术,2007,30(12):25-28. WANG Ying,CHENG Han-wen,WU Le-nan.Signal modulation mode identification based on spectral correlation characteristics[J].Information Technology,2007,30(12):25-28.(in Chinese)
[9]吴月娴,葛临东,许志勇.常用数字调制信号识别的一种新方法[J].电子学报,2007,35(4):782-785. WUYue-xian,GELin-dong,XUZhi-yong.ANovel Identification Method for Commonly Used DigitalModulations[J].Acta Electronica Sinica,2007,35(4):782-785.(in Chinese)
[10]李少凯,董斌,刘宁.基于谱线特征的MPSK调制识别[J].通信技术,2010,43(8):127-128. LIShao-kai,DONGBin,LIUNing.Modulation Recognition of MPSKSignals Based on Spectrum Line Feature[J].Communications Technology,2010,43(8):127-128.(in Chinese)
ZHOUMin was born in Chengdu,Sichuan Province,in 1987. She received the B.S.degree in 2010.She is now a graduate student.Her research direction is digital signal processing.
Email:mz0730@qq.com
冯全源(1963—),男,江西景德镇人,西南交通大学微电子研究所所长、博士生导师、IEEE高级会员,主要研究方向为数字、模拟、射频与混合信号集成电路设计,数字系统设计和嵌入式系统研究,现代天线技术、RFID技术(物联网技术)等。
FENGQuan-yuan was born in Jingdezhen,JiangxiProvince,in 1963.He is now the Director of Institute of Microelectronics as well as the Ph.D.supervisor in Southwest Jiaotong University,and also an IEEE seniormember.His research interests include digital,analog,RF andmixed-signal IC design,digital system design and research of embedded systems,modern antenna technology and RFID technology.
Email:fengyuanyuan@163.com
A Novel Identification M ethod for Digital M odulations
ZHOU Min,FENGQuan-yuan
(Institute of Microelectronics,Southwest Jiaotong University,Chengdu 610031,China)
By analysing the characteristics of digitalmodulations′power spectrum and higher order spectral,the method to calculate the higher spectrum is improved.On this base,new feature parameters are proposed.Combined with the instantaneous statistical feature parameter and support vectormachine(SVM)classifier,the automatic identification of digital communication signals in the AWGN channel is achieved.Simulation results show that the extracted feature parameters have good anti-noise performance as well as robustness to the change of modulation parameters.In consideration of the impact of pulse shaping,when the SNR value is greater than 12 dB,the lowest correct identification rate of the single-type signal is greater than 98.5%,and the average recognition rate is above 99.5%.
modulation identification;spectral analysis;feature extraction;support vectormachine;pulse shaping
The National Natural Science Foundation of China(No.60990320,60990323);The National High-tech R&D Program(863 Program)of China(2012AA012305)
TN911.72
A
10.3969/j.issn.1001-893x.2012.04.019
周敏(1987—),女,四川成都人,2010年获学士学位,现为硕士研究生,主要研究方向为数字信号处理;
1001-893X(2012)04-0518-05
2011-12-21;
2012-02-27
国家自然科学基金资助项目(60990320,60990323);国家高技术研究发展计划(863计划)项目(2012AA012305)
