基于最小二乘融合估计的双星时频差定位✴

彭华峰，夏畅雄，曹金坤

（西南电子电信技术研究所，成都610041）

基于最小二乘融合估计的双星时频差定位✴

彭华峰，夏畅雄，曹金坤

（西南电子电信技术研究所，成都610041）

针对单参考站条件下具有测量误差和星历误差时定位精度不高的特点，提出了一种基于多次观测数据的最小二乘融合估计定位算法，该算法无需增加观测条件即可有效提高辐射源定位精度。分析了测量误差、星历误差对单参考站单次定位及融合定位精度的影响，推导了测量误差、星历误差对定位误差的传递公式，提出了含星历误差影响的最小二乘融合估计加权算法。通过Monte-Carlo仿真验证了误差分析结果和定位算法，并比较了加权最小二乘估计定位和单次定位的性能。仿真试验表明：在相同观测精度条件下，加权最小二乘融合定位可极大地提高辐射源定位精度，最大提高10倍以上。

双星；时差频差；定位；估计；数据融合

1 引言

测量信号的到达时频差对目标进行定位是最重要的定位技术之一［1-4］。利用两颗卫星测量上行信号的到达时频差可以实现对地面辐射源定位，在导航、遥感及干扰源定位等方面有广泛的应用［3-4］。

利用同步轨道双星对地面进行定位时，由于卫星与辐射源距离远、相对运动较小、信号信噪比低等因素影响，定位精度比较低，在一些应用中通常难以同时找到满足条件的多颗卫星进行测量以进一步提高定位精度。工程实践中，为了克服星历误差及转发器时延等的影响，通常需要利用多个参考站校正误差影响［3-4］，但要满足同时多参考站条件要求相对比较苛刻，影响了系统实际效能的发挥。如何在现有双星定位条件下，通过融合多次观测数据进行融合估计实现单参考站条件下的辐射源定位，充分发挥单参考站条件下的定位能力是目前定位系统所需要解决的重要难点。

本文通过详细推导误差传递方程，将星历误差传递到测量误差后，然后取误差协方差的倒数为权值进行加权最小二乘融合估计，提高单参考站条件下定位精度，并通过计算机仿真比较了加权融合估计和非融合估计的定位精度，验证加权最小二乘融合估计算法的有效性。

2 双星定位原理

2.1 定位原理

双星定位原理为：利用两颗卫星接收到达信号的时频差（TDOA／FDOA），联立地球椭球方程可以求解得到目标的位置向量。

假设t时刻目标位置为Rs，参考站位置为Rr，主星位置为Rm，邻星的位置为Rn，则测量方程为

式中，rij=Ri-Rj，vij=Vi·j（Ri-Rj）／Ri-Rj，（i=m，n；j=r，s），Vij=Vi-Vj为相对速度向量；vij为相对速率；c是电磁波在空间的传播速度，ri（i =m，n）为卫星i与地面辐射源的距离。

此外，地球球面为椭球面，其曲面方程为

式中，a=6 378.14 km、b=6 356.755 km分别为地球的长短半径。

2.2 单次定位算法

基于单个时刻的两个观测量求解地面目标的位置时，已经提出了多种算法，如最大似然估计法、牛顿迭代算法等。本文给出牛顿迭代算法做单次定位仿真。

令

3 融合估计定位原理［5］

3.1 误差传递方程

对测量方程两边全微分可得

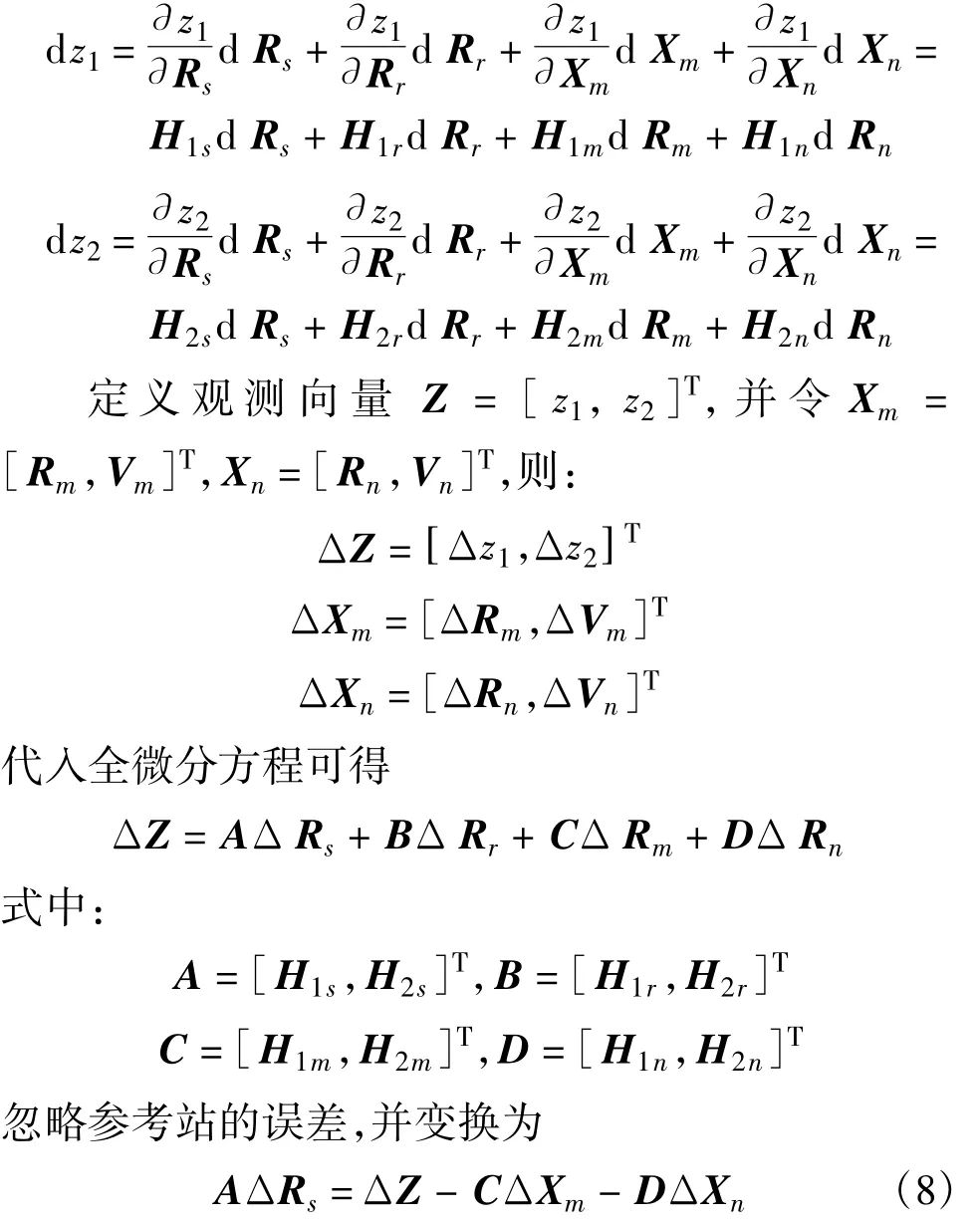
上式即为绝对星历误差表示时的误差方程。

本文采用相对星历误差进行分析。令相对星历误差为

式中，G=C+D。式（9）即为相对误差表示时的误差方程。

3.2 加权最小二乘融合定位算法

假设测量误差、主星星历误差和邻星星历误差的协方差矩阵分别为Cov（ΔZ）、Cov（ΔXm）和Cov（ΔδX），则误差方程右边等价为一个新的观测量ΔY，其协方差为

由加权最小二乘估计理论可知，取观测量的测量误差的协方差的倒数为其权值时估计效能最好，因此上式表明当有星历误差时，需要将星历误差传递到测量误差后，取传递后的测量误差协方差的倒数为权值才能实现最优估计。设W为Cov（ΔY）的对角线元素的倒数，则估计结果为

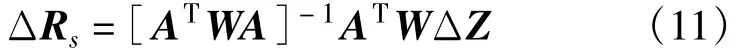
4 仿真分析

为了分析双星时频差对地面辐射源的定位，利用STK仿真产生了两颗同步轨道卫星的星历并随机生成了一个地面目标。模拟生成真实的测量参数，并分别对测量数据和卫星星历加正态高斯分布的随机噪声。假设卫星星历为正态分布的随机噪声是合理的，这是因为卫星星历可以通过实时测量和几何解算得到（如三站测距定位等），通过几何解算得到的星历符合正态高斯分布。测量数据和星历数据的采样间隔为1min。本文所有研究都是在该仿真条件下进行的。

4.1 单次定位仿真

采用Monte-Carlo分别仿真了在无星历误差、无相对星历误差和有相对星历误差条件下双星定位系统对辐射源的定位误差，如图1～3所示。设定的参数中，测量精度为300m、0.1 Hz，主星星历误差为20 km和2m／s，相对星历误差为5 km和0.5m／s。

图1 无星历误差时单次定位Monte-Carlo仿真Fig1Monte-Carlo simulation of positioning withoutephemeris error

图2 无相对星历误差时Monte-Carlo仿真Fig.2 Monte-Carlo simulation of positioning without relative ephemeris error

图3 有相对星历误差时的Monte-Carlo仿真Fig.3 Monte-Carlo simulation of positioning with relative ephemeris error

从仿真结果可以看出，主星星历误差对定位结果影响很大，相对星历误差对定位结果影响更大。当无星历误差时，单次定位误差在100 km以内；无相对星历误差时，单次定位误差在250 km以内；存在相对星历误差时，单次定位误差达到600 km。

4.2 融合定位仿真分析

采用60组数据进行融合估计，图4～6对应无星历误差、无相对星历误差和有相对星历误差时的Monte-Carlo仿真结果。图中虚线圈对应定位误差椭圆。从Monte-Carlo仿真结果可以看出，利用该加权估计算法得到的定位误差仍然满足高斯分布，验证了该加权估计方法的正确性。

对比图1～3可知，通过融合估计后，定位精度得到极大提高。当无星历误差时，定位精度由100 km提升至10 km以内；无相对星历误差时，定位精度由250 km提升至15 km以内；有星历误差时定位精度由600 km提升至100 km以内。

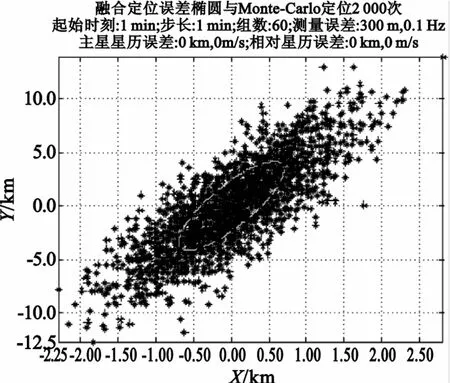
图4 无星历误差时融合定位Monte-Carlo仿真（60组数据融合）Fig.4 Monte-Carlo simulation of fusion positioning withoutephemeris error（60 observations fused）

图5 无相对星历误差时融合定位Monte-Carlo仿真（60组数据融合）Fig.5Monte-Carlo simulation of fusion positioning without relative ephemeris error（60 observations fused）

图6 有相对星历误差时融合定位Monte-Carlo仿真（60组数据融合）Fig.6Monte-Carlo simulation of fusion positioning with relative ephemeris error（60 observations fused）

5 结论

通过推导单参考站条件下融合定位的误差传递方程，证明当存在星历误差时，需要将星历误差传递到测量误差，取传递后的测量误差方差倒数进行加权。理论分析和Monte-Carlo定位仿真结果均表明，基于该加权方法的最小二乘估计算法在无星历误差时，定位精度由100 km提高至10 km；无相对星历误差时，定位精度由250 km以内提高到15 km以内；有相对星历误差时，定位精度由600 km以内提高到100 km以内。

本文从理论上分析和计算机仿真研究了具有随机星历噪声条件下观测数据加权融合估计算法，但利用网上公开星历时的最优加权估计算法是下一步需要研究的问题。

［1］Ho K C，Xu Wenwei.An Accurate Algebraic Solution for Moving Source Location Using TDOA and FDOA Measurements［J］.IEEE Transactions on Signal Processing，2004，52（9）：2453-2463.

［2］Ho K C，Lu Xiaoning，Kovavisaruch L.Source Localization Using TDOA and FDOA Measurements int the Presence of Receiver Location Errors：Analysis and Solution［J］.IEEE Transactions on Signal Processing，2007，55（2）：684-696.

［3］Ho K C，Chan Y T.Geolocation of a known altitude object from TDOA and FDOA Measurements［J］.IEEE Transactions on Aerospace and Electronic Systems，1997，33（3）：770-783.

［4］Haworth D P，Smith N G，Bardelli R.Interferrence localization for EUTELSAT Satellites-The First European Transmitter Location System［J］.International Journal of SatelliteCommunications，1997，15（2）：155-183.

［5］韩崇昭，朱洪艳，段战胜，等.多源信息融合［M］.北京：清华大学出版社，2006. HAN Chong-zhao，ZHU Hong-yan，DUAN Zhan-sheng，etal.Multisource information fusion［M］.Beijing：Tsinghua U-niversity Press，2006.（in Chinese）

PENG Hua-feng was born in Xinhua，Hunan Province，in 1979.He received the M.S.degree from Sichuan University in 2006.He is now an engineer and currently working toward the Ph.D.degree.His research concerns target location，tracking and satellite orbitmeasurement.

Email：hualong913＠sina.com

夏畅雄（1979—），男，湖南岳阳人，2008年于西南电子电信技术研究所获博士学位，现为高级工程师，主要研究方向为目标定位等；

XIA Chang-xiong was born in Yueyang，Hunan Province，in 1979.He received the Ph.D.degree from Southwest Electronics and Telecommunication Technology Research Institute in 2008.He is now a senior engineer.His research concerns target location.

Email：xiaxiong＠sohu.com

曹金坤（1980—），男，安徽阜阳人，2006年于信息工程大学获硕士学位，现为博士研究生，主要研究方向为信号处理、目标定位等。

CAO Jin-kunwasborn in Fuyang，AnhuiProvince，in 1980. He received the M.S.degree from Information Engineering University in 2006.He is currently working toward the Ph.D.degree.His research interests include target location，tracking and satellite orbit measurement.

Email：kingquencho＠gmail.com

TN 电子技术、通信技术类核心期刊表

Geo-location Using Dual-satellite′s TDOA and FDOA Data by Least Square Fusion Estimation

PENGHua-feng，XIAChang-xiong，CAO Jin-kun
（Southwest Electronics and Telecommunication Technology Research Institute，Chengdu 610041，China）

Aiming at the problem ofgeo-location with only one reference station，which has feature of low position precision when there aremeasurement error and ephemeris error，a Least Square（LS）estimationmethod is proposed here by fusingmulti-time′s observation，bywhich the location accuracy can be greatly improved without increasing the observation conditions.In condition of one reference station，when measurement error and ephemeris error are added，the one observation geo-location method and multi-observation geo-location method are studied.The influence of observation error and ephemeris error is analysed.The equation of error transfer from observation error and ephemeris error to geo-location error is derived.A weighted algorithm for LS estimation geo-location is proposed and compared with the one observation geo-location algorithm.By Monte -Carlo simulation，the analysis conclusion and weighted LSestimation geo-location algorithm are proved，and also the performance ofone-observation andmulti-observation algorithm is compared.Simulation result shows that theweighted LSmulti-observation geo-location estimator can greatly improve the location precision.The best result shows thatmulti-observation algorithm can be 10 times better than one-observation geo-location algorithm.

dual-satellite；time and frequency difference of arrival；location；estimation；data fusion

序号刊名序号刊名1电子学报23半导体技术2光电子、激光24激光杂志3液晶与显示25光通信技术4红外与激光工程26电路与系统学报5电波科学学报27电子元件与材料6红外与毫米波学报28电子科技大学学报7电子与信息学报29应用光学8通信学报30应用激光9北京邮电大学学报31数据采集与处理10激光与红外32光电子技术11西安电子科技大学学报33光通信研究12系统工程与电子技术34电子器件13现代雷达35电信科学14红外技术36电讯技术15微电子学37电子技术应用16半导体光电38电视技术17光电工程39压电与声光18微波学报40重庆邮电大学学报.自然科学版19激光技术41功能材料与器件学报20信号处理42南京邮电大学学报.自然科学版21激光与光电子学进展43微纳电子技术22固体电子学研究与进展

TN971

A

10.3969／j.issn.1001-893x.2012.04.003

彭华峰（1979—），男，湖南新化人，2006年于四川大学获硕士学位，现为博士研究生、工程师，主要研究方向为目标定位、跟踪和测轨等；

1001-893X（2012）04-0435-05

2011-12-21；

2012-02-17