基于锁频环与锁相环相结合的载波跟踪技术✴

许志鹏，崔琛，余剑

（电子工程学院信息系，合肥230037）

基于锁频环与锁相环相结合的载波跟踪技术✴

许志鹏，崔琛，余剑

（电子工程学院信息系，合肥230037）

针对锁频环与锁相环各自在载波跟踪方面的优点与不足，设计了一种基于Costas环的锁频环与锁相环相结合的载波跟踪环路。基于锁频环与锁相环各自锁定时残余频差与残余相差都接近于0的原因，提出了mc、mpe两个阈值，当阈值满足设定的条件时，载波跟踪环路自适应地选择相应的工作状态。仿真结果表明，在阈值达到设定的条件时环路能够正确地实现工作状态的转换，在多普勒频移为固定值以及阶跃函数时能进行准确的跟踪，达到了设计目的。

相干接收机；载波跟踪；锁频环；锁相环

1 引言

相干接收机中，恢复出与载波同频同相的相干载波是接收机系统设计的关键技术之一。载波跟踪环路通常采用锁频环（FLL）和锁相环（PLL）来实现。锁相环在低动态时具有较高精度和较好的抗噪性能，但是在较大多普勒频偏条件下锁相环必须增加环路带宽才能对载频进行跟踪，而这也意味着更多噪声的进入，必然减低跟踪精度；而锁频环虽然直接跟踪载波频率，具有较好的动态性能，但是跟踪的精度不如锁相环。

目前文献对锁相环的设计讨论较多，对锁相环和锁频环的结合应用讨论较少。文献［1］虽然也采取了锁相环与锁频环联合跟踪载波的方式，但是并没有对环路工作状态切换条件作深入细致的讨论，且多普勒频移为固定值以及阶跃函数的情况没有进行仿真。基于此，针对锁相环与锁频环各自的优缺点，为了实现对载波的精确跟踪，设计了一种锁相环与锁频环相结合的载波跟踪架构，并提出一种使用阈值md和mpe的判断方法：环路工作过程中不断检测频差大小，当多普勒频移大于设定值时采用锁频环进行频率跟踪；反之锁相环进行相位补偿，实现对载波相位的精确跟踪。

2 载波跟踪环架构

设计的载波跟踪环架构如图1所示，该跟踪环主要由积分清除器、锁频环、锁相环以及状态鉴别器组成，其中状态鉴别器的主要功能是对I（k）、Q（k）两路正交值进行相应的运算，以判明环路当前工作状态和应该转入的状态。

设图中x（n）、Voc（n）、Vos（ n）分别为

则

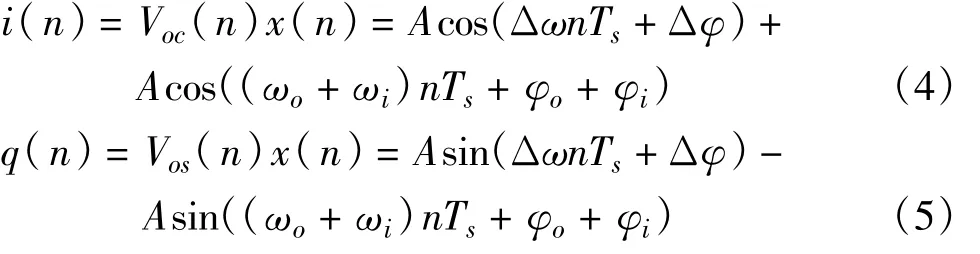
其中，ωi与ωo分别为输入输出频率，φi与φo分别为输入与输出信号的初始相位，Ts为采样间隔，Δω=φi -φo为输入输出频差，Δφ=φi-φo为初始相差。

积分清除器实质上是一个低通滤波器［3］，设积分长度为N，则

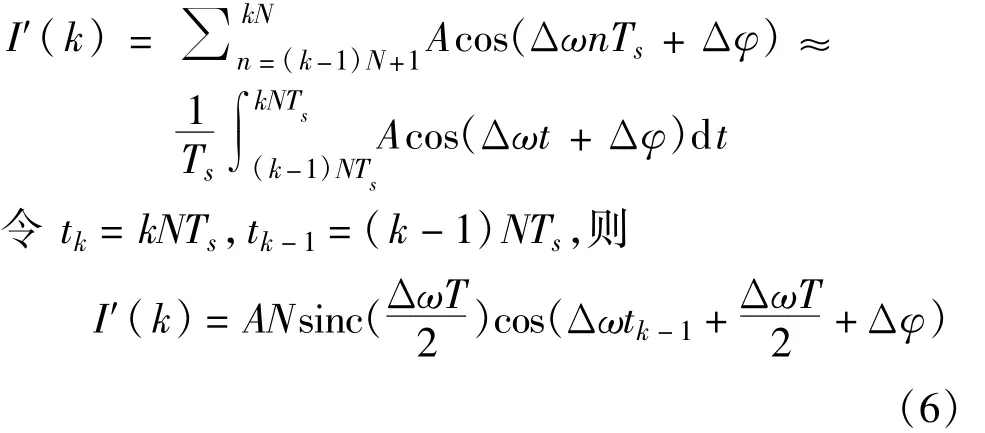
其中，T=tk-tk-1=NTs。

同理：

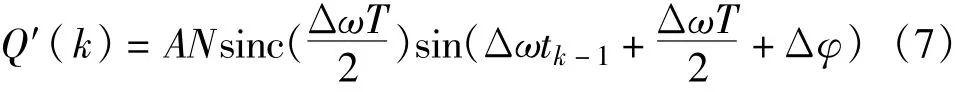
3 载波环路的具体设计

3.1 锁频环的设计

3.1.1 鉴频器的设计

叉积鉴频法是目前鉴频器中常用的鉴频算法，叉积鉴频器如图2所示，由图可知：

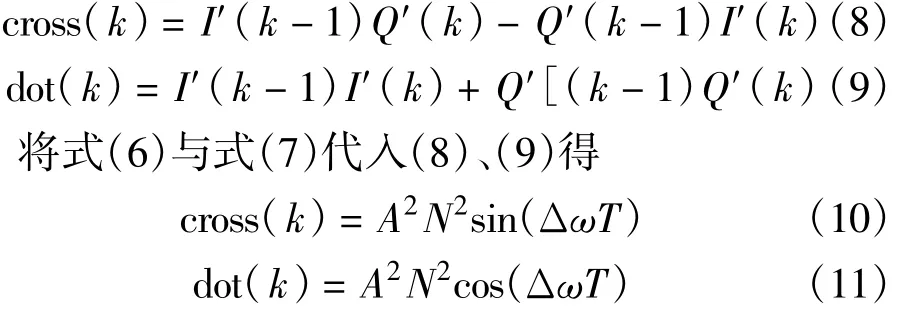
则利用反正切法鉴频可得

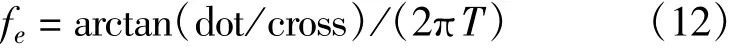
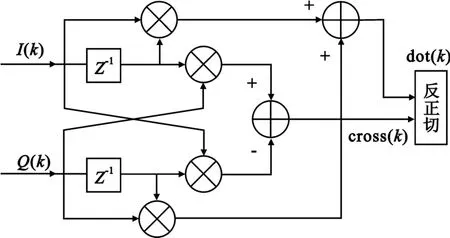
图2 叉积鉴频器Fig.2 Cross-dot frequency discriminator

3.1.2 锁频环滤波器设计

锁频环环路滤波器采用二阶杰夫-瑞廷滤波器，其模拟形式如图3所示。

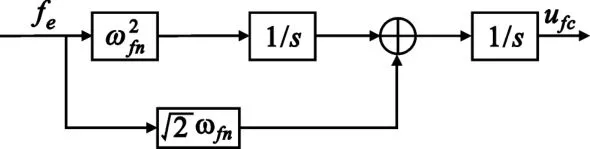
图3 锁频环环路滤波器模拟形式Fig.3 Analog form of loop filter of PLL

式中，ωfn为锁频环环路滤波器带宽。使用双线性变

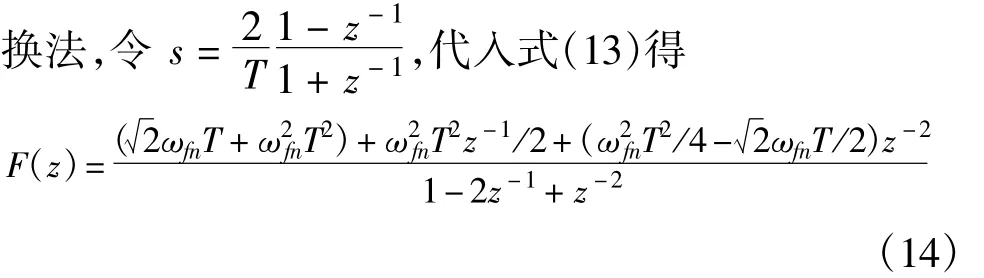
由图可得滤波器传递函数

设输入频率为465.4 kHz，T=1 ms，ωfn=4 Hz，频偏400 Hz，采用上述架构，锁频环的频率跟踪性能如图4所示。

图4 锁频环频率跟踪性能Fig.4 FLL′s performance of tracking frequency

3.2 锁相环的设计

采用反正切法鉴相器，即：

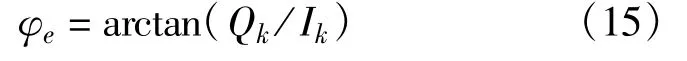
锁相环环路滤波器采用理想二阶环［6］，如图5所示，图中C1、C2分别为

图5 理想二阶环框图Fig.5 Ideal second-order loop filter′s architecture

设输入信号频率为465.01 kHz，T=1ms，ωpn= 40 Hz，频偏10 Hz，采用上述架构，锁相环的相位跟踪与频率跟踪性能如图6所示。

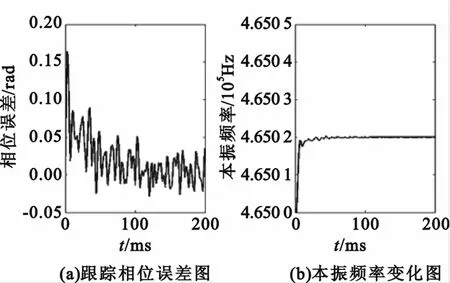
图6 锁相环频率跟踪性能Fig.6 PLL′s performance of tracking frequency

3.3 状态鉴别器的设计

设计的载波跟踪环路的基本思想是在频偏超过设定值时采用锁频环对频率进行粗锁定，当频偏减小到设定值以下时转入锁相环对进行精确锁定。下面分两个方面对状态转换条件进行讨论。

（1）锁频环向锁相环转换条件

由式（10）、（11）可知，在锁频环工作状态下，当Δω足够小时，cross（k）≈0，dot（k）≈A2N2。当这两个条件同时满足时说明频差已足够小，则转入锁相环工作。令

作为判决条件（mc为mean dot的缩写）。当Δω足够小时mc≈0。考虑到噪声影响，实际仿真中当md＜0.05时即转入锁相环工作。

（2）锁相环向锁频环转换条件

由式（9）和式（10）可知，当转入锁相环工作时，I′（k）=AN cos（Δφ），Q′（k）=AN sin（Δφ），当锁相环稳定时，Δφ趋近于零，当频率产生较大变化时，Δφ也产生较大变化。令

作为判决条件（mpe为mean phase error的缩写，Δφk为k时刻鉴相器输出）。由于刚进入锁相环工作时初始相差可能较大，若是此时即开始判断则很容易造成误判断。所以应该舍弃初始的鉴相值，待锁相环稳定后再取Δφ的均值mpe，当mpe＞ε时（0＜ε＜1，文中取ε=0.6），载波跟踪环路由锁相环转入锁频环工作。

4 仿真验证

输入信号频率465.1 kHz，采样率1 MHz，初始频差100 Hz，在250ms处发生200 Hz频率阶跃，用所设计的载波跟踪环对频率进行跟踪。在高信噪比（5 dB）与低信噪比（-10 dB）情况下对转换条件的仿真结果分别如图7与图8所示。

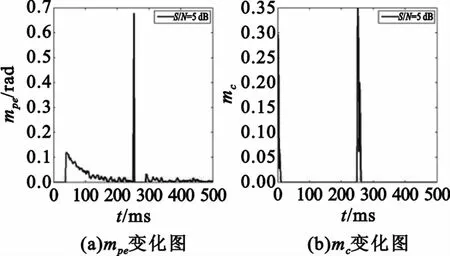
图7 高信噪比下阈值图Fig.7 Thresholds in high SNR

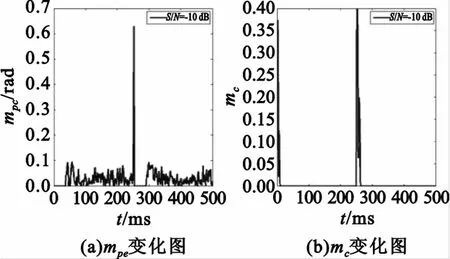
图8 低信噪比下阈值图Fig.8 Thresholds in low SNR

由图7（b）和图8（b）可知，在高低信噪比下，环路在刚开始的20ms内mc迅速减小，这是由于此时锁频环在工作，频差迅速减小。此时锁频环停止工作，锁相环开始起作用；在250ms处频率发生突变，鉴相值迅速增大，mpe也迅速增大，很快超过设定的ε，环路转入锁频环工作；之后mc又迅速减小，环路再次进入锁相环工作状态。因此，由仿真可见，文中所设计的mc与mpe阈值起到了控制环路工作状态的作用。

在高低信噪比下对载波频率跟踪的结果如图9和图10所示。

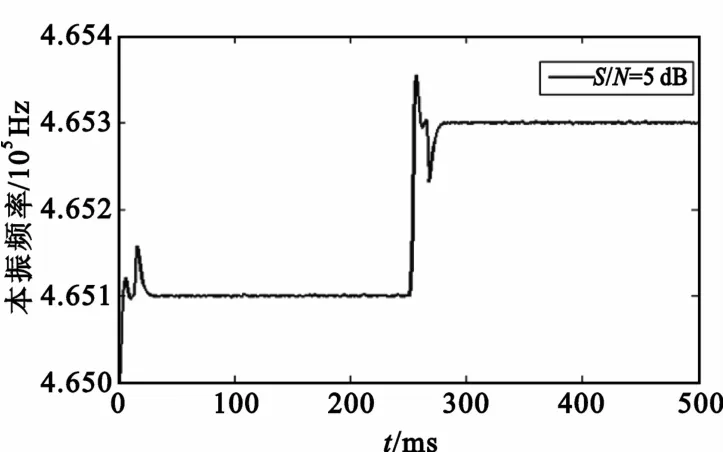
图9 高信噪比下联合载波跟踪结果Fig.9 Performance of carrier-tracking of the loop in high SNR

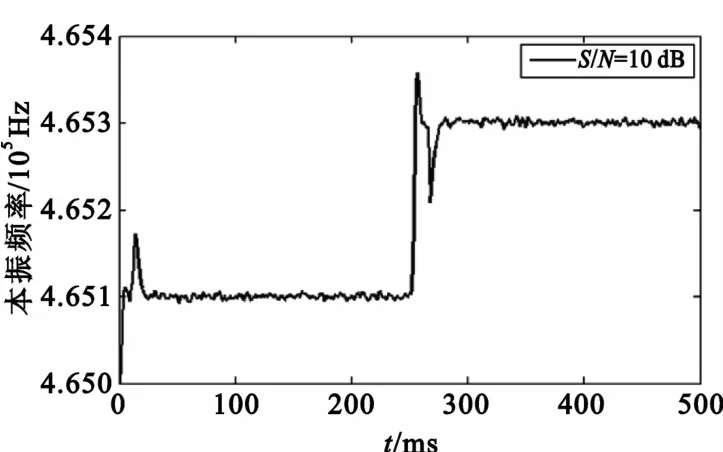
图10 低信噪比下联合载波跟踪效果Fig.10 Performance of carrier-tracking of the loop in low SNR

图中突起部分是由于在频率从发生阶跃到再次被锁定这一过程中输入输出相差累积较大，从而鉴相输出较大，因此频率变化率也较大。随着环路的工作，频率渐趋稳定。

5 结论

本文设计了一种锁频环与锁相环相结合的载波跟踪环路，基于锁频环与锁相环在跟踪载波达到稳定状态时残余频差与相差接近于0的原因，提出了两个阈值，用以判决载波跟踪环路该以何种方式对载波进行跟踪。与单独使用锁相环对载波进行跟踪相比，该方法既快又准确。目前我们只是对多普勒频偏为固定值和阶跃值的情况进行了仿真，对于多普勒频偏为一次斜升函数和二次斜升函数等其他情况下如何对载频进行跟踪的问题尚未研究，这将是我们下一步工作的重点。

［1］王兰芳，吴长奇，高秀英.基于FLL与PLL级联的高动态载波跟踪技术［J］.电子测量技术，2009，34（3）：25-27. WANG Lan-fang，WUChang-qi，GAOXiu-ying.Technology of carrier tracking for high dynamic signals based on FLL and PLL cascade［J］.Electronic Measurement Technology，2009，34（3）：25-27.（in Chinese）

［2］王雪芹，郑郁正.一种高动态载波跟踪方案的仿真分析［J］.成都信息工程学院学报，2009，24（2）：118-121. WANG Xue-qin，ZHENGYu-zheng.Analysis of a carrier tracking scheme for high-dynamic signal［J］.Journal of Chengdu University of Information Technology，2009，24（2）：118-121.（in Chinese）

［3］Natali F D.AFC Tracking Algorithms［J］.IEEE Transactions on Communications，1984，25（8）：935-947.

［4］王兰芳.基于FLL和PLL的载波跟踪技术研究［D］.秦皇岛：燕山大学，2009 WANG Lan-fang.The Study Of Carrier Tracking Based on FLL And PLL［D］.Qinhuangdao：Yanshan University，2009.（in Chinese）

［5］罗大成，王仕成，王明福.载波跟踪算法综述［J］.系统仿真学报，2008，20（22）：6023-6028. LUODa-cheng，WANG Shi-cheng，WANG Ming-fu. Overview of Carrier Tracking Algorithms［J］.Journal of System Simulation，2008，20（22）：6023-6028.（in Chinese）

［6］吴华明，苏雁泳，刘爱军.锁相环与锁频环在数字Costas环中的应用［J］.科学技术与工程，2010，10（19）：4645-4650. WUHua-ming，SU Yan-yong，LIU Ai-jun.Application of PLL and FLL in the Digital Costas Loop［J］.Science Technology and Engineering，2010，10（19）：4645-4650.（in Chinese）

［7］罗大成，王仕成，刘志国.一种基于FQFD／FLL／PLL的混合载波跟踪算法［J］.航天控制，2009，27（1）：10-14. LUODa-cheng，WANG Shi-cheng，LIU Zhi-guo.A Hybrid Carrier Tracking Algorithm Based on FQFD，FLL and PLL［J］.Aerospace Control，2009，27（1）：10-14.（in Chinese）

XU Zhi-peng was born in Lianshui，Jiangsu Province，in 1985.He received the B.S.degree in 2007.He is now a graduate student.His research interests include AGC and AFC.

Email：279671691＠qq.com

崔琛（1962—），男，安徽合肥人，教授，主要研究方向为通信系统仿真。

CUIChen was born in Hefei，AnhuiProvince，in 1962.He is now a professor.His research concerns communication system simulation.

Carrier Tracking Based on Combination of FLL and PLL

XU Zhi-peng，CUIChen，YU Jian
（Department of Information，Electronic Engineering Institute，Hefei230037，China）

A carrier-tracking loop is designed on the base of respective advantages and disadvantages of FLL and PLL on carrier-tracking.Two thresholds（mcand mpe）are proposed according to the reason thatwhen FLL and PLL catch the frequency，the restof frequency error and phase error are approximately equal to zero.When the two thresholds satisfy the given conditions，the loop will choose work state automatically.Simulation shows thatwhen the two thresholds satisfy the given conditions，the loop can switch work state correctly，and carrier can all be tracked whenever the Doppler frequency is a constant value or a step equation of time，and the aim of design is realized.

coherent receiver；carrier tracking；FLL；PLL

TN973.3

A

10.3969／j.issn.1001-893x.2012.04.027

许志鹏（1985—），男，江苏涟水人，2007年获学士学位，现为硕士研究生，主要研究方向为自动增益控制与自动频率控制；

1001-893X（2012）04-0558-04

2011-12-21；

2012-02-29