一种改进的基于EMD分解的超宽带信号消噪算法✴
2012-07-01王海梁熊华钢吴庆刘成
王海梁,熊华钢,吴庆,刘成
(北京航空航天大学电子信息工程学院,北京100191)
一种改进的基于EMD分解的超宽带信号消噪算法✴
王海梁,熊华钢,吴庆,刘成
(北京航空航天大学电子信息工程学院,北京100191)
针对低信噪比超宽带信号的消噪问题,提出一种改进的基于经验模式分解(EMD)的消噪算法。该算法首先对含噪信号进行EMD分解,得到多个固有模态函数(IMF)分量,然后选取高阶IMF重构原信号,达到消噪的目的。针对对UWB信号的IMF重构过程中阶数阈值难以确定的问题,通过数值仿真的方法,得到信号分量和噪声分量在不同阶IMF上的能量分布特性;在对所得特性进行分析的基础上,设计了一种数据自适应的阶数阈值选取算法,解决了EMD消噪中的阶数阈值选取问题。仿真结果表明,EMD消噪算法能够在较低信噪比下提供平均10 dB的信噪比增益,可以有效地对超宽带信号进行消噪。
超宽带;信号消噪;经验模式分解
1 引言
脉冲超宽带(Ultra-wideband,UWB)无线电技术具有高隐蔽性、抗多径效应、较高的距离分辨力等优良特性,在通信、定位和雷达等领域都有应用,是当前无线电技术的一个研究热点[1-2]。受发射功率的限制,脉冲UWB信号通常信噪比较低,因此,对UWB信号的消噪是UWB信号处理中的一个重要课题。
处理信号消噪问题的传统方法是利用Fourier变换或者小波变换消噪。由于UWB信号具有高带宽、低功率谱的特性,利用Fourier变换进行消噪的方法对UWB信号难以取得较好的消噪效果;而小波消噪需要预先选择好基函数,对于不同种类的UWB脉冲波形,很难找到一种通用的基函数选择方法,目前,尚未有针对UWB信号的有效消噪方法的相关文献见诸报道。
经验模态分解(Empirical Mode Decomposition,EMD)是近年来提出的一种时频处理算法[3],该算法无需预先指定基函数,特别适用于对非平稳、非线性信号的处理。文献[4-7]提出对EMD分解得到的固有模态函数(Intrinsic Mode Function,IMF)进行筛选,选取部分IMF重构原信号可以达到消噪的目的。
本文将IMF重构消噪的思想应用于超宽带信号消噪问题的解决中。针对重构过程中IMF的阶数阈值选取问题,设计了一种自适应的阈值选取算法。该选取算法以超宽带信号的各阶IMF能量分布特性为基础,从数据中直接提取阈值信息,无需对信号和噪声做特殊假设。IMF重构方法和自适应的阈值选取方法相结合,构成了基于EMD分解的超宽带信号消噪方法。通过对人工合成信号和实际采集信号的仿真实验,验证了该消噪方法的有效性。
2 超宽带信号消噪问题
2.1 脉冲超宽带信号
脉冲超宽带信号由一系列时间上不连续的窄脉冲构成,脉冲的宽度通常在纳秒或者百皮秒的量级,根据使用目的的不同,脉冲的幅度或者位置可以被编码,形成移位的窄脉冲序列。脉冲超宽带信号一般具有较大的带宽和较低的功率谱密度,受到发射功率的的限制,一般接收到的超宽带信号具有较低的信噪比。图1给出了文献[1]中描述的跳时超宽带信号原始脉冲串和附加了噪声的含噪信号波形图。
2.2 超宽带信号的消噪
已知含噪信号y(t)=x(t)+n(t),原始信号为x(t),n(t)是高斯白噪声。信号消噪即求对原始信号的估计信号^x(t),使得均方误差

尽可能小。
为衡量消噪的效果,定义信号输入信噪比Sin和消噪后的输出信噪比Sout分别为
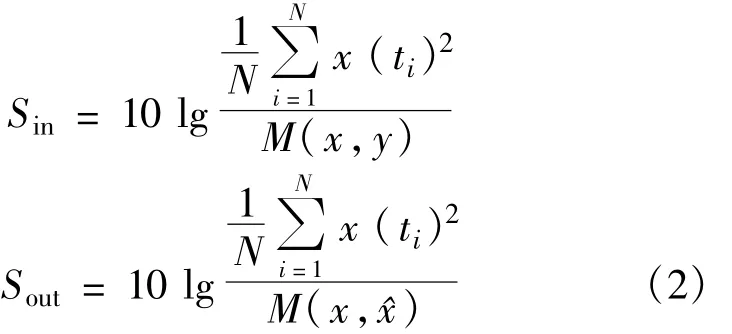
那么可以用信噪比增益

来描述消噪的性能。
3 EMD分解
EMD方法利用一个迭代的筛分过程将一个给定的信号s(t)分解成L个IMF分量hi(t)和一个残余分量rL(t),每个IMF代表了信号s(t)在某个时间尺度或者频带上的细节。每个IMF要满足两个条件[3]:一是IMF中的极值点和过零点的数目最多相差1,二是上包络线和下包络线的局部均值为0。
筛分过程按照从高频到低频的顺序形成不同阶的IMF,最先得到的IMF(低阶IMF)具有最高的频率,最后得到的IMF(高阶)具有最低的频率。EMD的主要优点是筛分过程是数据驱动的,不需要预先构造基函数。
由文献[3],IMF的筛分过程是一个迭代的过程,每次迭代筛分出一个IMF分量,对于第j次迭代,rj-1(t)为当前残余分量,并且当j=1时,有r0(t)=s(t)。迭代过程如下:
(1)令hj,i(t)←rj-1(t),i←1;(2)求hj,i(t)的极大值和极小值,并利用3次样条插值求得极大值确定的上包络线和极小值确定的下包络线;
(3)求上下包络线的均值mj,i(t);
(4)更新hj,i+1(t)←hj,i(t)-mj,i(t),i←i+1;
(5)判断hj,i(t)是否满足IMF的两个条件,若满足,则hj(t)=hj,i(t)为第j阶IMF分量,若不满足,重复步骤(2)~(4);
(6)更新残余值rj=rj-1(t)-hj(t),j←j+1,如果rj(t)中的极值点少于两个,终止迭代,否则,从第1步开始继续迭代过程。
筛分过程结束后,原信号s(t)可以表示成分解得到的各阶IMF hj(t)和残余值rL(t)的组合:
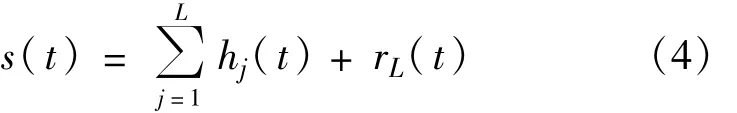
式中,hj(t)代表不同频段的信号分量,rL(t)代表信号整体的变化趋势。
4 基于EMD的超宽带信号消噪
4.1 IMF重构消噪
EMD过程将信号分解成一系列代表不同特征频率的IMF分量,低阶IMF代表信号的高频部分,高阶IMF对应信号的低频部分。由文献[5,8]可知,对于白噪声,EMD分解后噪声的能量将主要集中于高频IMF分量中。当对过采样的含噪信号进行EMD分解时,由文献[6],可以认为噪声的主要能量分布在高频IMF中(前几阶IMF),信号的主要能量分布在低频IMF中(后几阶IMF),并随着阶数的降低而递减。因此,可以认为存在某个阶数阈值th,对于任何阶数大于等于该阈值的IMF,其中信号部分占据主要成分;阶数小于该阈值的IMF中,噪声占据主要成分。
通过滤除阶数小于该阈值的IMF,利用高阶IMF和趋势分量重构原信号,可以达到消噪的目的,重构信号可以表示为
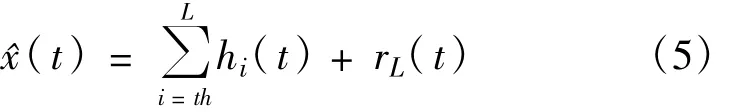
能否选择合理的阶数阈值是有效实现该重构算法的关键。在实际应用中,由于带宽和采样率的变化,使得对于不同信号的分解,有效部分对应的阶数不固定,无法预先确定。下面通过对超宽带含噪信号和噪声的EMD分解结果的对比分析,给出一种阈值选取算法。
4.2 超宽带信号IMF重构的阈值选取
目前,EMD方法还没有比较完备的解析解释,大多数针对EMD的研究结果都是在数值仿真的基础上通过对实验结果进行总结得出的。本文也采取计算机数值仿真的方式研究超宽带信号EMD分解后不同阶IMF的能量分布特性,从中找出选取阶数阈值的方法。
仿真采用跳时UWB信号,采用高斯0阶脉冲作为基本脉冲波形,脉冲宽度为1 ns,脉冲的重复周期为10 ns,信号总长度为100 ns,对该信号叠加高斯白噪声,形成信噪比为-5 dB的含噪信号。仿真在20 GHz和50 GHz两种采样率下进行,在每种采样率下各运行了10 000次仿真,每次仿真生成含噪信号和噪声,并分别进行EMD分解,求各阶IMF的能量,最后对10 000次结果求平均值,得到了含噪信号和噪声的各阶IMF能量分布图,如图2和图3所示。

图2 采样率20 GHz时噪声和含噪信号的各阶IMF能量对比(对数坐标)Fig.2 IMF energy of noise and noised signal at 20 GHz sample frequency(semi-log axis)
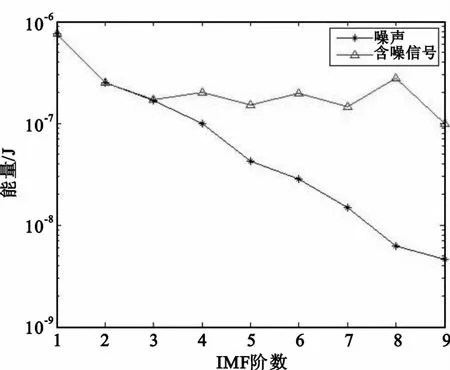
图3 采样率50 GHz时噪声和含噪信号的各阶IMF能量对比(对数坐标)Fig.3 IMF energy of noise and noised signal at 50 GHz sample frequency(semi-log axis)
从图中可得,对于噪声的EMD分解,各阶IMF的能量随着阶数的增加而逐渐减弱;在对数坐标轴中,各阶IMF的能量近似构成一条下降的直线,说明各阶IMF的能量近似构成等比数列,这与文献[8]中对白噪声IMF的研究结果是一致的。
对于含噪信号,其前几阶IMF和噪声的IMF曲线基本重合,当阶数到达某个值时(20 GHz采样率时为3,50 GHz采样率时为4),两条曲线的差值出现跃变,含噪信号该阶IMF的能量远大于对应的噪声IMF的能量,说明在该阶IMF中,信号能量开始占据主要成分,这个阶数即需要求的阶数阈值。
令含噪信号第i阶IMF的能量密度为Es,i,噪声第i阶IMF的能量密度En,i, 两者的比值为

那么,当βi大于某个常数λ(一般可采用1.5)时,可以认为该IMF中信号能量占据主要成分。于是,可以选择满足βi>λ的最小i值为阶数阈值。
在实际应用中,无法准确获得噪声的IMF,也无法获得En,i的准确值。在过采样的条件下,可以假设含噪信号的前两阶IMF和噪声前两阶IMF近似相等,利用噪声IMF能量的等比数列特性可以获得对En,i的 估计:
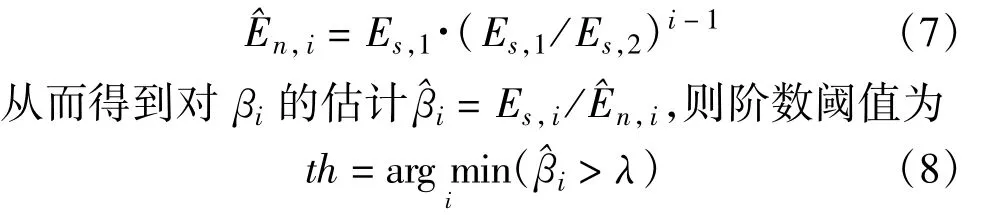
采用这种阈值选取方法,可以直接由获得的信号中估计阈值,不需要对噪声分布的先验知识,因此这是一种自适应的阈值选取方法,具有较好的灵活性和实用性。
4.3 EMD消噪算法描述
由上面分析,超宽带信号的EMD消噪算法可以表述如下:
(1)对含噪信号进行EMD分解,得到IMF集合{hi(t),i=1,2,…,L};
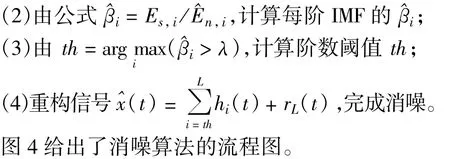
5 仿真与分析
为了考察EMD消噪算法对超宽带信号的消噪效果,本文进行了一系列的仿真实验。
实验一采用计算机合成的、被白噪声污染的跳时UWB信号做为待处理的含噪信号,用0阶高斯脉冲做为基本脉冲,脉冲的重复周期取10 ns,脉宽1 ns,信号长度取3个脉冲重复周期。分别在不同的信噪比条件下对EMD消噪算法的性能进行了仿真。作为对比,同时采用小波消噪方法对相同的信号进行了仿真。
表1给出了不同信噪比条件下,EMD消噪和小波消噪算法的信噪比增益。可以看到,使用EMD消噪算法,在不同信噪比下,平均可以获得10 dB左右的信噪比增益;在相同信噪比条件下,可以比小波消噪算法获得3 dB以上的信噪比增益。
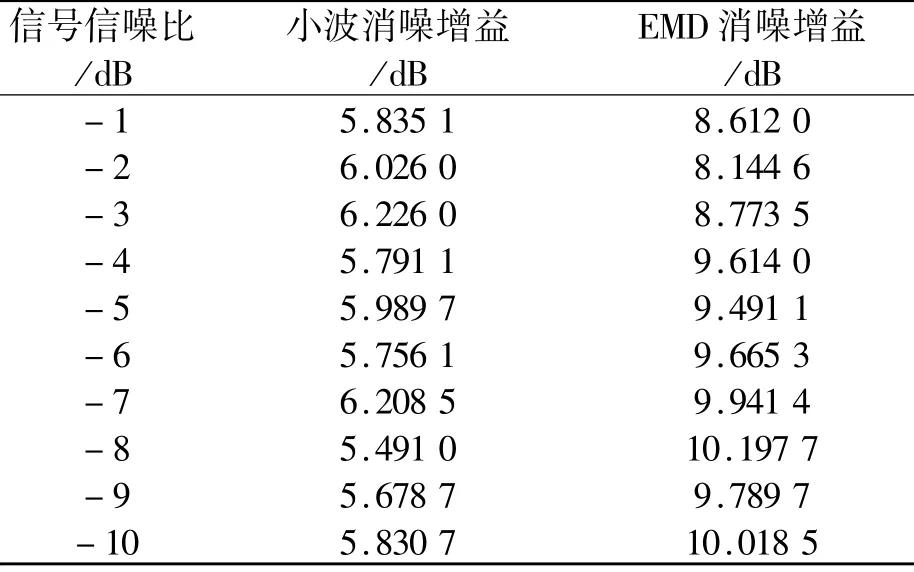
表1 消噪后信噪比增益Table 1 SNR gain after denosing
图5给出了信噪比为-5 dB时原始信号、含噪信号和消噪后的信号对比图。从图中可以看到,相比小波消噪,EMD消噪算法可以消除信号波形中由噪声引起的毛刺,更有效地突出原始窄脉冲的轮廓和位置。
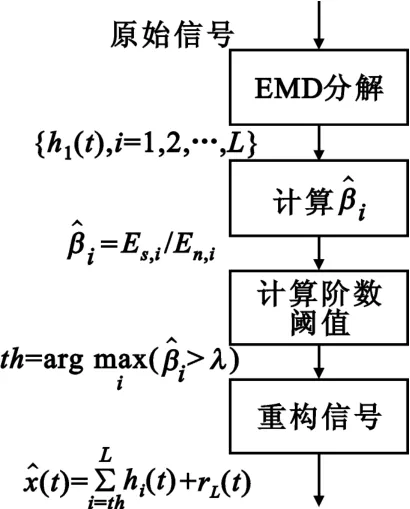
图4 消噪算法流程图Fig.4 Flow chart of proposed denosing algorithm
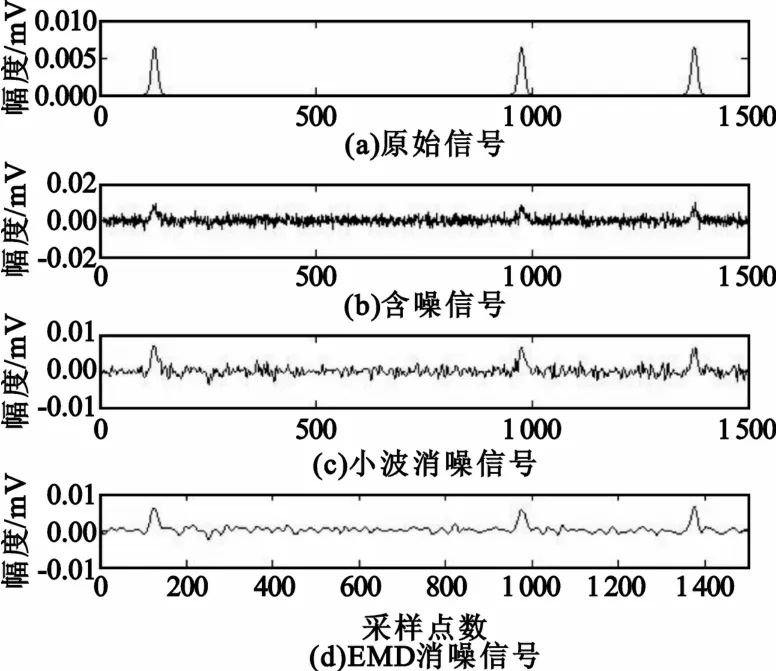
图5 -5 dB输入信噪比信号的消噪结果Fig.5 Denoising resultswhen SNR=-5 dB
实验二采用了一段实际采集的含噪超宽带脉冲信号,该信号来自于某超宽带穿墙雷达[9]的脉冲回波,雷达发射脉冲为类高斯脉冲,脉宽1.4 ns,采样率为20 GHz。回波中含有多个从不同反射体反射回来的脉冲,因为发射功率受限,并且回波信号穿墙后受到较大衰减,使得接收信号的信噪比较低。图6给出了含噪回波信号和采用小波消噪和EMD消噪后的信号对比图。从图中可以看到,采用EMD消噪算法,将附加在脉冲回波中的大量噪声毛刺滤除,消噪后的信号与原信号相比,脉冲轮廓更加清晰,相邻脉冲之间的界限更明显。在原信号中,由于信噪比较低,一些低能量的脉冲回波被埋藏在噪声水平线下,无法分辨,而EMD消噪后,这些低能量脉冲可以被清晰地分辨出来。EMD消噪算法增强了UWB雷达对回波脉冲的分辨能力。

图6 UWB穿墙雷达回波信号消噪效果Fig.6 Denoising results of UWB radar signal
6 结论
本文提出了一种利用EMD分解来解决超宽带信号消噪问题的算法。该算法通过部分选取EMD分解得到的高阶IMF分量重构原始信号,从而达到消噪的目的;该算法针对各阶IMF的能量分布特征,给出一种自适应的阶数阈值选择方法,解决了IMF重构中的阈值选择问题。仿真结果表明,该算法在低信噪比下具有较好的消噪效果,可以有效地应用在低信噪比超宽带通信和雷达信号处理领域,具有较好的实用前景。如何降低对信号采样率的要求和如何获得高效的硬件实现可以作为该问题的进一步研究方向。
[1]Win M,Scholtz R.Ultra-wide bandwidth time hopping spread-spectrum impulse radio for wirelessmultiple access communications[J].IEEE Transactions on Communications,2000,48(4):679-691.
[2]Di Benedetto,Guerino Giancola.超宽带无线电基础[M].北京:电子工业出版社,2005. Di Benedetto,Guerino Giancola.Understanding Ultra Wide Band Radio Fundamentals[M].Beijing:Publishing House of Electronics Industry,2005.(in Chinese)
[3]Huang N E,Shen Zheng,Long SR,etal.The empiricalmode decomposition and the hilbert spectrum for nonlinear and non -stationary time series analysis[J].Proceedings of the Royal Society A,1998,454(1971):903-995.
[4]Flandrin P,Goncalves P,Rilling G.Detrending and denoisingwith empiricalmode decompositions[C]//Proceedings of the 2004 European Signal Processing Conference.Vienna,Austria:IEEE,2004:1581-1584.
[5]Flandrin P,Goncalves P,Rilling G.Empiricalmode decomposition as a filter bank[J].IEEE Signal Processing Letters,2004,11(2):112-114.
[6]Boudraa A,Cexus JC.EMD-based signal filtering[J]. IEEE Transactions on Intsrument and Measurement,2007,56(6):2196-2202.
[7]Elgamel SA,Soraghan JJ.Using EMD-FrFT filtering tomitigate very high power interference in chirp tracking radars[J]. IEEESignal Processing Letters,2011,18(4):263-266.
[8]Wu Z,Huang NE.A study of the characteristics ofwhite noise using the empiricalmode decompositionmethod[J].Proceedings of the Royal Society A,2004,460(2046):1597-1611.
[9]Wu Qing,Zheng Kuangyu,Li Qiao,et al.Design and implementation of sub-GHz transmitterfor ultra-wideband throughwall radar[C]//Proceedings of 2010 IEEE International Conference on Ultra-wideband.Nanjing:IEEE,2010:1-4.
WANG Hai-liang was born in Shenyang,Liaoning Province,in 1983.He is currently working toward the Ph.D.degree.His research interests include UWB communicationsand signalprocessing.
Email:gabbar@163.com,gabbar@ee.buaa.edu.cn
熊华钢(1961—),男,1998年获博士学位,现为教授、博士生导师,主要研究方向为航空电子网络、超宽带通信;
吴庆(1984—),男,博士研究生,主要研究方向为超宽带通信和信号处理;
WUQingwas born in 1984.He is currentlyworking toward the Ph.D.degree.His research interests include UWB communications and signal processing.
刘成(1985—),男,博士研究生,主要研究方向为航空电子网络、超宽带通信。
LIUCheng was born in 1985.He is currently working toward the Ph.D.degree.His research interests include avionics networks and UWB communications.
A Novel Denoising Algorithm for UWB Signals Based on Em pirical M ode Decom position
WANGHai-liang,XIONGHua-gang,WU Qing,LIU Cheng
(School of Electronics and Information Engineering,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)
To solve the problem of denoising ultra-wideband(UWB)signals,a novel denosing algorithm based on empiricalmode decomposition(EMD)is proposed.The algorithm first uses EMD to decompose the noised signal into intrinsicmode functions(IMF),then uses high order IMFs to reconstruct the original signal.In order to get the proper threshold in IMF reconstructing,the energy distribution property of each IMF is examined by numeric simulation.According to the distribution property,a data-adaptive algorithm on choosing the threshold is proposed.Simulation results show that the proposed denoising algorithm can improve the signal signal-tonoise ratio(SNR)by 10 dB under low SNR conditions.
ultra-wideband;signal denoising;empiricalmode decomposition
-gangwas born in 1961.He
the Ph.D. degree in 1998.He is now a professor and also the Ph.D.supervisor.His research interests include avionics networks and UWB communications.
The National Natural Science Foundation of China(No.60879024)
TN911.6
A
10.3969/j.issn.1001-893x.2012.04.008
王海梁(1983—),男,辽宁沈阳人,博士研究生,主要研究方向为超宽带通信和信号处理;
1001-893X(2012)04-0461-05
2011-12-20;
2012-02-20
国家自然科学基金资助项目(60879024)
