拉索高强镀锌平行钢丝摩擦系数的进一步确定

陈 璨，郑 罡，燕海蛟，杜 渊

(1.重庆交通大学土木建筑学院，重庆400074;2.招商局重庆交通科研设计院有限公司，重庆400067)

平行钢丝斜拉索的局部弯曲应力的大小直接与弯曲刚度的大小取值、钢丝间是否发生滑移相关。斜拉索是否发生滑移主要取决于索体内部钢丝之间的极限摩擦剪应力与斜拉索钢丝间受到的剪应力的大小。因此，准确测定斜拉索高强镀锌平行钢丝摩擦系数值非常重要。

对斜拉索钢丝摩擦系数值的初步研究表明，在自重作用下和小荷载作用下，斜拉索内平行钢丝间摩擦系数均值为0.210 8［1］，但该研究所施加的正压力值过小，无法达到实桥中拉索所受正压力值的大小。故笔者对斜拉索内高强镀锌平行钢丝摩擦系数进行了进一步的确定。影响摩擦系数的因数很多，如正压力的大小、接触时间、平滑程度、润滑情况、滑动速度等。由于斜拉索内高强镀锌平行钢丝每层钢丝平均受到正压力的大小不相同［2］，故笔者在研究中主要考虑正压力大小对平行钢丝摩擦系数值的影响，其它影响因素暂不予考虑。

1 正压力对摩擦系数的影响

根据固体力学相关知识，表观接触面积一定时，正压力N越大，实际接触面积S0越大，并和正压力成正比:

式中:S0为实际接触面积;s为正压力为0时的实际接触面积;N为正压力;ΔS0为实际接触面积增量;ΔN为正压力增量。

设单位实际接触面积上的分子引力P0，则接触面上的合分子引力为:

它相当于物体增加了重量负载，等效正压力Neff为:

根据摩擦二项式定律，滑动摩擦力fr和等效正压力Neff成正比，即:

式中:fr为滑动摩擦力;μ为摩擦系数;Neff为等效正压力;P0为分子引力;N0为接触面上的合分子引力;其他符合同前。

由摩擦二项式定律即式(4)可得:

而一般意义的摩擦系数为:

即，表观摩擦系数随着正压力N的增大而减小，从而不是恒量［3］。蒋浩民，等［4］采用平板摩擦试验研究了正压力对镀锌钢板摩擦系数的影响，实验证实了摩擦系数随着正压力N的增大而减小。

总之，正压力对摩擦系数的影响与实际接触面积有关，一般情况下是摩擦系数随正压力增加而降低，然后趋于稳定［5］。

2 实验方法

2.1 加压方式及实验装置的确定

本实验装置是在此前实验装置的基础上经设计改装而成的，利用此前实验所用的1#、2#两块钢槽固定钢丝，如图1。

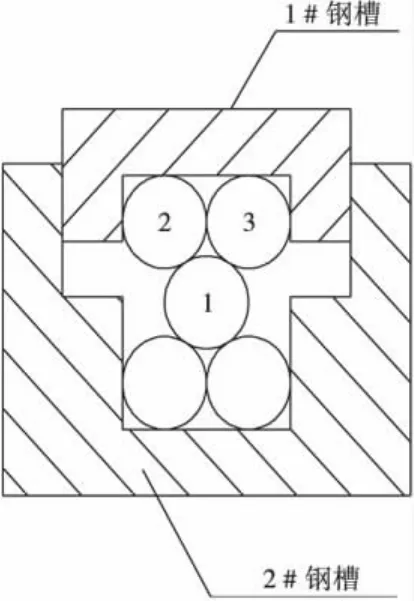
图1 实验所用1#、2#钢槽Fig.1 The 1#，2#steel tank used in experiments

采用两枚M10×200螺栓对钢槽均匀地施加正压力，为了较精确地给螺栓加压，采用螺距为1mm的M10标准螺距螺栓［6］。实验装置如图2。

图2 实验装置Fig.2 Experimental device

将两根M10螺栓螺杆穿过自制的承压梁，并将螺母栓在螺杆上。用扳手拧螺母时，螺母对承压梁产生压力，此压力将通过梯形钢板传递至钢槽上，从而实现对钢槽内钢丝的加压。试验中，设置梯形钢板的目的是为了实现对钢槽的均匀加压，根据力基本沿45°方向传递原则，将梯形钢板设计成两底角为45°［图2(b)］。在梯形钢板和钢槽之间放置橡胶板，目的是防止加压过程中梯形钢板与钢槽之间的打滑，且有利于将梯形钢板所受到的的力均匀传递至钢槽。在试验中，为了使整个装置能够悬挂起来，在1#和2#上挖两个 φ8的孔［图2(b)］。

把装置悬挂起来［图2(c)］，当用扳手拧紧螺帽时，产生的压力通过承压梁一直传至梯型钢板，通过梯型钢板对钢槽均匀加力。在加压过程中，较难控制螺栓对钢槽所加的力的大小。但明显的，当对螺栓加压时，螺栓会因此而产生相应的应变。所以，为了较精确地控制螺栓加力的大小，在螺栓中部位置黏贴电阻应变片，螺栓上应变片布置如图3。通过电阻应变片测得的钢筋的平均应变值，由应变值可反算出所加压力值的大小，此压力值也可视为螺栓对承压梁所加的压力值，也为螺栓对钢槽所加的压力值。

图3 螺栓的应变片布置Fig.3 Strain gauge on the bolt arrangement figure

2.2 加压值的大小

经过层间累加之后，内层单根钢丝间挤压力可高达40 kN/m［7］。由试验用钢丝的受力长度 10 mm，确定出对1#钢丝加压范围为300～4 000 N，在此压力范围加压，足以模拟斜拉索实际工作中拉索的真实受力状态了。在300～4 000 N范围内，对应各个级别的正压力，分别进行拉拔实验，得出相应的钢丝摩擦系数值。本次实验中，由于时间和精力有限，在所得数据在统计上有一定保证率的前提下，将所加正压力300～4 000 N范围分成17个级别，分别进行了拉拔实验。

3 实验开展与结果讨论

3.1 实验开展

本实验测试螺栓应变所用的应变片为电阻位为120 Ω的BE120-4AA的应变片，灵敏度 K=2.23±0.01。将两张应变片对称地布置在用于加力的螺栓的中部(图3)。为了进行温度补偿，取一螺栓，在其上黏贴补偿片(补偿片的布置如图4、图5)。

图4 补偿片上应变片布置Fig.4 Strain gauge on the compensator arrangement figure

图5 补偿片上应变片布置实物Fig.5 Strain gauge on the compensator physical map

本实验利用美国DEWE-501数据采集系统进行应变的采集，实验采用单倍电桥接线法接线。实验方案布置如图6。

图6 实验方案布置Fig.6 Experimental arrangement

3.2 实验结果讨论

根据实验数据得出斜拉索高强镀锌平行钢丝摩擦系数随正压力变化的变化趋势如图7。

图7 摩擦系数随正压力变化的变化趋势Fig.7 Friction coefficients changing with the positive pressure

从图7可看出:随着正压力的增大，高强镀锌钢丝的摩擦系数值总体上成下降趋势。此实验结果与理论推导得出的结论——表观摩擦系数不是恒量，而是随着正压力的增大而减小——是相吻合的。随着正压力的增大，一直增大到1 700 N附近，高强镀锌钢丝的摩擦系数值下降十分显著，可能的原因是由于一定的正压力有助于钢丝与钢丝之间达到良好的润滑并抑制表面的粗糙。但当压力继续增大，直到4 000 N左右时，图中出现了一段非常平缓的下降段。即当正压力增大到较大值时摩擦系数的降幅明显减缓了。出现此下降段的原因可能是:随着压力的继续增加，钢丝与钢丝之间的接触面积会有所增加，在较高压力下镀锌层对摩擦系数的影响已经明显减小了。

4 结论

笔者利用自行设计的装置对钢丝施加一定的正压力。测定出一定压力下一系列钢丝间的摩擦系数值，描述出摩擦行为表现和摩擦系数变化趋势为:随着正压压力的增大，斜拉索内高强镀锌平行钢丝的摩擦系数明显降低，但当压力增大到较大值时摩擦系数的降幅明显减缓。

［1］李红，郑罡，陈璨.斜拉索内平行钢丝间摩擦系数的确定［J］.重庆交通大学学报:自然科学版，2011，30(2):196－199.Li Hong，Zheng Gang，Chen Can.Determination of friction coefficients between steel wires in stay cables［J］.Journal of Chongqing Jiaotong University:Natural Science，2011，30(2):196－199.

［2］Zheng Gang，Li Hong.Normal stress between steel wires in the stay-cable［J］.Applied Mechanics and Materials Journal，2011，50/51:541－546.

［3］刘亚民.摩擦力与摩擦系数的几点性质［J］.乌伦贝尔学院学报，2006，14(4):67 －68.Liu Yamin.Some qualities of friction and friction modulus［J］.Journal of Hulunbeier College，2006，14(4):67－68.

［4］蒋浩民，陈新平，俞宁峰，等.正压力和滑动速度对镀锌钢板摩擦系数的影响［J］.锻压技术，2005，30(增刊1):129 －132.Jiang Haomin，Chen Xinping，Yu Ningfeng，et al.Effects of contact pressure and sliding velocity on the frictional coefficient of zinccoated sheets［J］.Forging ＆ Stamping Technology，2005，30(supp1):129－132.

［5］贾毅朝，摩擦与摩擦系数的分析［J］.运城学院学报，2006，24(2):60－61.Jia Yichao.Analysis of friction and friction factors［J］.Journal of Yuncheng University，2006，24(2):60－61.

［6］GB/T 5782—2000六角头螺栓［S］.北京:中国标准出版社，2001.

［7］李红.斜拉索内钢丝间联合工作模式对局部弯曲应力的影响［D］.重庆:重庆交通大学，2010.

［8］黄平.摩擦学教程［M］.北京:高等教育出版社，2008.

［9］PTI.Recommendation for Stay Cable Design，Testing and Installation［R］.Phoenix，Arizona:Post-Tensioning Institute，2001.

［10］杨骏，王刚雷，黄瑶.电镀锌板摩擦系数的影响因数分析［J］.精密成形工程，2009，1(3):14 －17.Yang Jun，Wang Ganglei，Huang Yao.The analysis on the influence factors of frictional coefficient of zinc-coated sheet［J］.Journal of Netsshape Forming Engineering，2009，1(3):14－17.

［11］杨兴，张敏，周水兴.影响矩阵法在斜拉桥二次调索中的应用［J］.重庆交通大学学报:自然科学版，2009，28(3):508 －511.Yang Xing，Zhang Min，Zhou Shuixing.Application of influence matrix method to secondary cable-adjustment of cable-stayed bridges［J］.Journal of Chongqing Jiaotong University:Natural Science，2009，28(3):508－511.