连续刚构桥顺桥向非线性地震反应研究

曾金明，朱东生，张永水，张 洁

(重庆交通大学土木建筑学院，重庆400074)

连续刚构桥具有造型优美，行车舒适，造价低等优点，近年来在国内修建较多。由于连续刚构桥一般跨径较大，多采用薄壁高墩，地震反应较为复杂，其抗震性能也受到了研究人员的重视。如，范立础［1］曾对5座连续刚构桥用反应谱进行了线性地震反应分析，指出抗震设计的控制截面位置为墩底截面、主梁根部和跨中截面;李忠献，等［2］对一座4跨连续刚构桥进行了线性时程分析，计算了不同波速下其地震响应，讨论了行波效应对连续刚构桥地震响应的影响;陈星烨，等［3］对某高墩连续刚构桥进行了Pushover分析，讨论了连续刚构桥进行Pushover分析时应注意的一些问题;夏修身，等［4］采用集中塑性铰模型，计算了连续刚构桥的非线性地震响应;刘怀林，等［5］采用 Pushover方法，按 JTG/T B 02 －01—2008《公路桥梁抗震设计细则》［6］的要求，对某连续刚构桥的抗震能力进行了分析和验算。

分析现有的研究可以看出，目前多数研究是结合具体工程进行连续刚构桥的线性地震响应分析，讨论相关工程的抗震性能，缺少深入的规律性研究。仅有个别学者采用集中塑性铰模型对连续刚构桥进行过非线性时程分析。

笔者对某高墩大跨连续刚构桥进行了较为深入的非线性时程地震响应分析，计算模型中桥墩采用纤维单元模拟。沿顺桥方向分别输入了不同场地上的实际地震记录，得到了不同场地条件下连续刚构桥顺桥向的非线性时程地震响应，发现了影响连续刚构桥非线性地震响应的一些因素和抗震设计中应注意的问题。

1 计算模型及输入的地震波

笔者以实际工程中的一座高墩大跨连续刚构桥为对象，该桥跨径布置为(90+166+90)m，桥宽12 m，主梁采用变高度预应力混凝土单箱单室箱梁，桥墩为单肢矩形薄壁空心墩，其中1号墩高70 m，2号墩高83 m。1号墩沿顺、横桥均采用1∶100放坡，桥墩沿顺桥的宽度为6.0～7.4 m，横桥向的宽度为6.6 ～8.0 m;2 号墩沿顺、横桥均采用 1∶80 放坡，桥墩沿顺桥向的宽度为6.000～8.075 m，横桥向的宽度为6.600～8.675 m。壁厚均为0.9 m。桥墩纵筋的配筋率在1.08%左右，桥墩墩顶、墩底15 m内箍筋的间距为0.1 m，其余范围的间距为0.15 m，箍筋采用φ16钢筋。桥梁所在场地为Ⅱ类场地，水平基本设计加速度为0.3 g。

1.1 单元模型

在进行结构非线性地震响应分析时，单元模型和恢复力曲线模型的选择非常关键。目前对于桥墩的非线性模拟多采用集中塑性铰单元和纤维梁单元［7］。

集中塑性铰方法具有使用简便的优点，适用于塑性铰位置及构件变形明确的场合。由于高墩的塑性铰位置并不明确，且沿墩高方向桥墩的轴力变化较大，因此采用更为精确的纤维模型模拟桥墩。

由于笔者重点分析该桥顺桥向的非线性地震反应，故桥墩纤维只针对顺桥向进行单向条形划分，纤维的划分见图1。主梁在地震中一般不会进入非线性，因此采用普通梁单元模拟，全桥计算模型见图2。

图1 桥墩纤维划分Fig.1 Sketch of pier cross section meshing

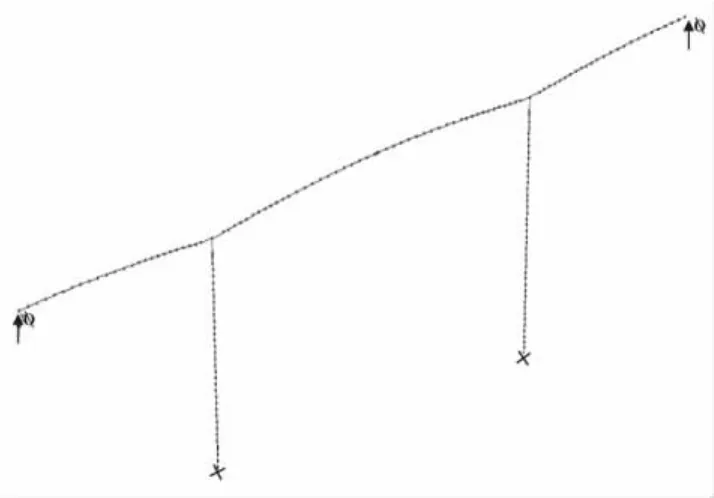
图2 计算模型Fig.2 Calculating model of the bridge

1.2 材料本构模型

恢复力曲线模型可以建立在材料应力－应变关系层次上，也可以建立在截面内力－变形关系层次上。通过分析所采用的单元模型和研究问题的特点，所选用的恢复力曲线模型是建立在材料应力－应变关系层次上的。

1.2.1 钢筋本构模型

钢筋采用理想弹塑性模型，其屈服应力取为335 MPa，弹性模量为 2.0E+5 MPa，极限应变设为0.05，钢筋本构关系见图3。

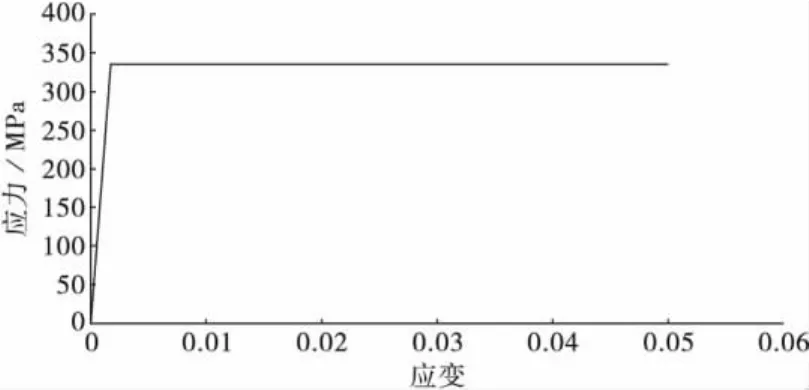
图3 钢筋应力－应变关系Fig.3 Stress-strain relationship of steel

1.2.2 混凝土本构模型

目前常用的混凝土本构模型有Mander模型［8］和Kent-Park模型。笔者采用Mander模型，该模型的本构关系与截面的形状和箍筋的配置等因素有关。根据桥墩截面的形状、箍筋配置，计算得到核心混凝土的屈服应力为32.4 MPa，屈服应变为0.003 9，极限压应力为38.56 MPa，极限应变为0.035，混凝土的本构关系如图4。

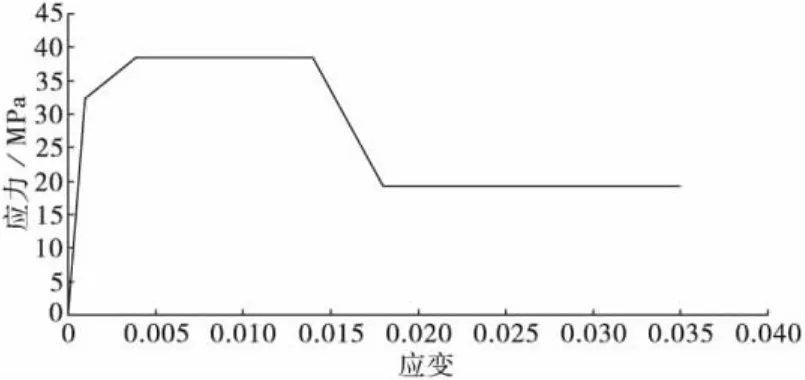
图4 混凝土应力－应变关系Fig.4 Stress-strain relationship of the confined concrete

混凝土滞回关系在PERFORM-3D软件中由能量退化系数来控制(图5)。能量退化系数是滞回曲线上退化滞回环的面积与非退化滞回环面积之比(图6)。能量退化系数可通过试验或者理论分析结果得到。根据Mander模型设定滞回关系中的卸载刚度和再加载刚度。

计算中结构的材料阻尼采用瑞利阻尼，阻尼比选择为5%。

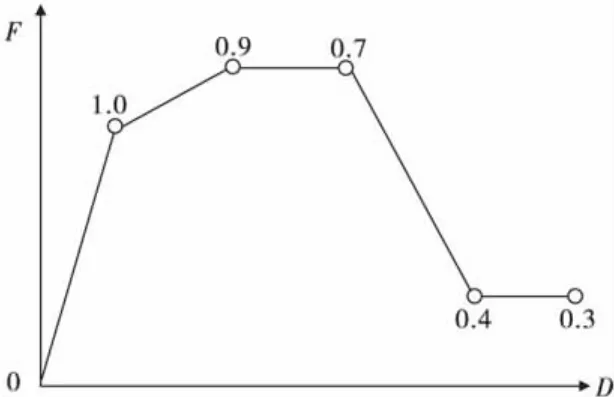
图5 混凝土能量退化系数Fig.5 Energy degradation factor of concrete

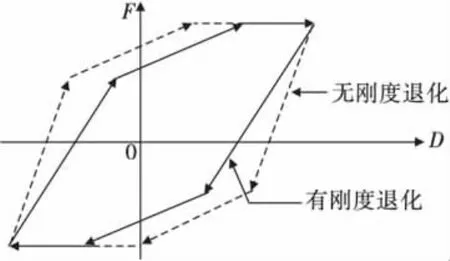
图6 刚度退化滞回环示意Fig.6 Sketch of hysteresis loop with stiffness degradation

1.3 地震波选择

为了研究场地条件对大跨高墩连续刚构桥地震响应的影响，选择3种类型场地上的地震波。3条波及其所代表的场地和加速度峰值区间见表1。3条波的加速度反应谱如图7。

表1 地震动记录Table 1 Earthquake records

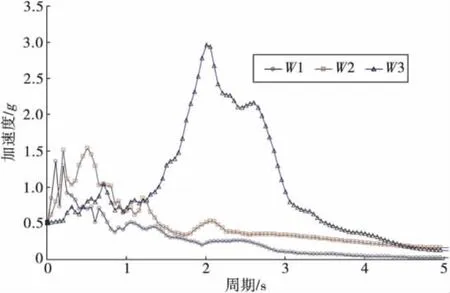
图7 地震动加速度反应谱图Fig.7 Response spectrum curves of earthquake waves

该桥所在场地的基本设计加速度峰值为0.3g，考虑E2地震作用时，根据文献［6］，将各条波的加速度峰值均调整为0.51g。

2 动力特性

按照建立的计算模型，首先计算了该桥的自振特性，其前5阶频率及振型特点如表2。从结果可以看出，该桥由于跨度较大，且桥墩较高，刚度相对较小，自振频率也相对较小;前5阶振型中多为横向振动，这是因为该桥的宽度只有12 m，横向刚度相对较小。

表2 前5阶阵型自振特性Table 2 Natural vibration characteristics of the first five modes

3 非线性时程响应结果及分析

根据前述的计算模型，采用PERFORM-3D程序，分别计算该桥在上述3条地震波作用下的线性和非线性时程响应。表3为计算得到的桥墩内力非线性、线性响应最大值;表4为墩顶位移响应最大值，由于本桥是连续刚构桥，两个桥墩在主梁的联系下沿顺桥方向同步变形，墩顶的顺桥向位移基本相同。图8为1号墩墩底弯矩－曲率滞回曲线。

表3 桥墩内力最大响应值Table 3 Maximum force of time-history of the piers

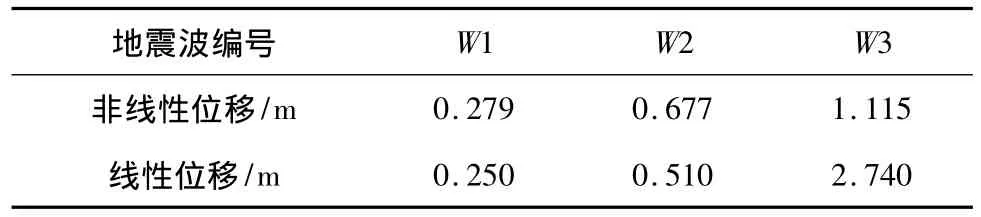
表4 墩顶位移时程响应最大值Table 4 Maximum displacement of time-history top of piers

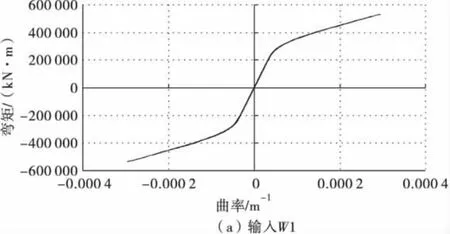
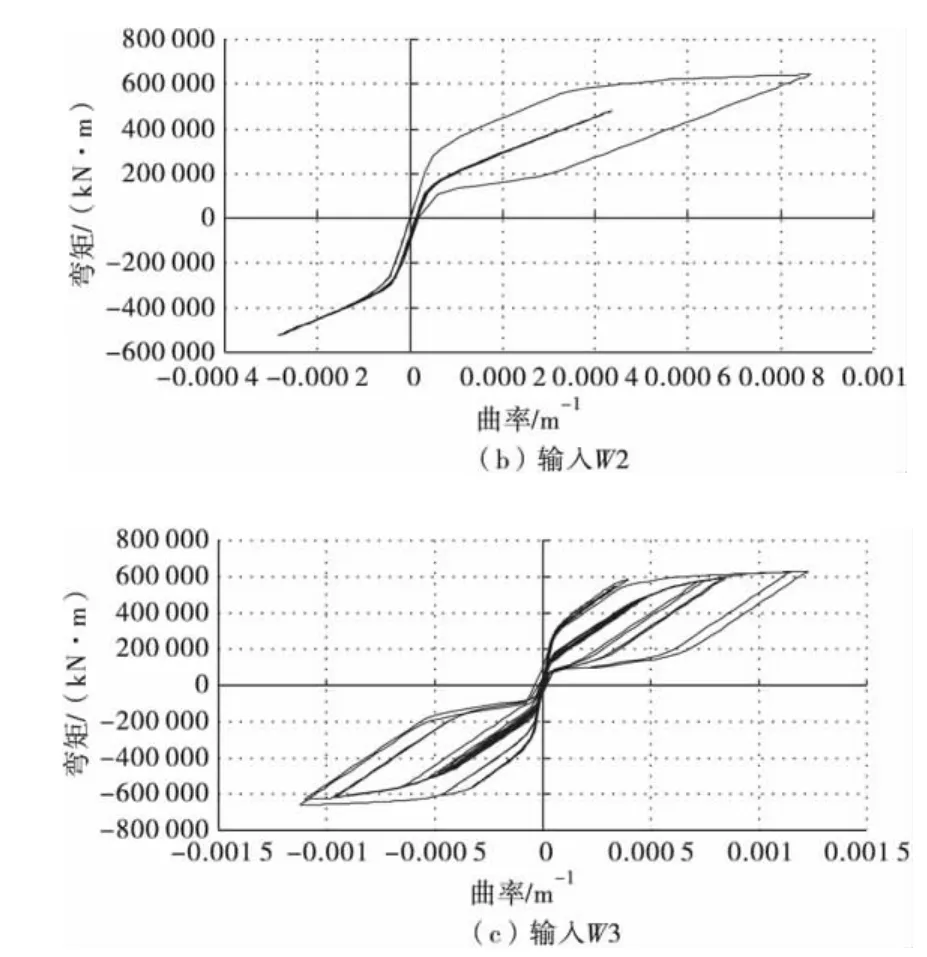
图8 1号墩墩底弯矩－曲率滞回曲线Fig.8 Moment-curvature hysteresis loop at the bottom of No.1 pier

3.1 场地条件对地震响应的影响

从表3中可以得出，在相同的场地条件下，1号墩墩顶剪力、弯矩和墩底的剪力都较2号墩的大，而1号墩墩底的弯矩较2号墩墩底弯矩小。由表3、表4可以看出，场地条件由中硬变得软弱时，桥墩内力的最大响应值、墩顶的位移都在增加。结合图8的墩底弯矩－曲率滞回曲线，可以看出，在中硬场地上，该桥桥墩出现了开裂，但没有发生屈服;在中软场地上，桥墩部分区域发生了屈服，但塑性变形较小，墩底截面曲率响应延性最大值小于3;在软土场地上，桥墩的非线性变形较大，墩底截面的曲率延性系数接近5。

虽然笔者只对一座桥用3条波进行了分析，但考虑到大跨高墩连续刚构桥的刚度普遍较小，周期偏大，因此从有利于抗震的角度考虑，高墩大跨连续刚构桥适宜修建在地质条件较好坚硬场地上，在高烈度地区的中软或软土场地上修建大跨高墩连续刚构桥时，需要认真处理其抗震问题。

3.2 线性结果与非线性结果的比较分析

比较表3中桥墩内力线性、非线性时程响应最大值可以发现，线性与非线性分析所得桥墩内力差异较大，且3条波作用下桥墩内力线性结果均较非线性结果大，这表明该桥在E2地震情况下，无论处于那类场地，都进入了非线性。

从线性分析内力结果可以看出，3条波的弯矩最大值均远超过了桥墩的弯矩极限承载能力，线性分析结果已不能反映E2地震下桥梁的真实响应。

比较3条地震波非线性响应的内力及位移最大值可以看出，随着地震波的不同，桥墩墩顶的位移成倍增长，而桥墩内力增长较慢。这是因为当桥墩进入塑性后，其刚度变得很小，即使在很小的荷载作用下，都会产生很大的位移。

比较线性与非线性墩顶位移响应最大值可以发现，在W1和W2地震波作用下，线性位移和非线性位移结果比较接近，而在W3地震波作用下，线性位移和非线性位移差异很大。这表明当桥墩处于弱非线性状态时(即非线性变形较小)，其位移响应符合等位移原则，而当桥墩处于强非线性状态时，等位移原则不一定成立。

3.3 墩高对桥墩地震响应的影响

分别计算了3类场地的地震波作用下的两桥墩墩底、墩顶弯矩－曲率滞回曲线。现以分析墩底非线性地震反应为例，列举了两桥墩墩底的最大曲率(表5)。

表5 墩底最大曲率Table 5 Maximum curvature at the bottom of piers/m－1

从表5可以看出，在3类场地的地震波作用下，1号墩墩底的最大曲率都比2号墩墩底的大。

图9为W3地震波作用下的两桥墩墩底的弯矩－曲率滞回曲线。由图9可以得出，输入W3时，1号墩墩底的最大曲率都比2号墩底的大，而1号墩墩底弯矩较2号墩的小。即对于墩高差异较大的连续刚构桥，矮墩的曲率都较高墩大。这是由于各墩墩顶顺桥向的位移相同，矮墩墩底的塑性铰区，就需要更大的转动能力。

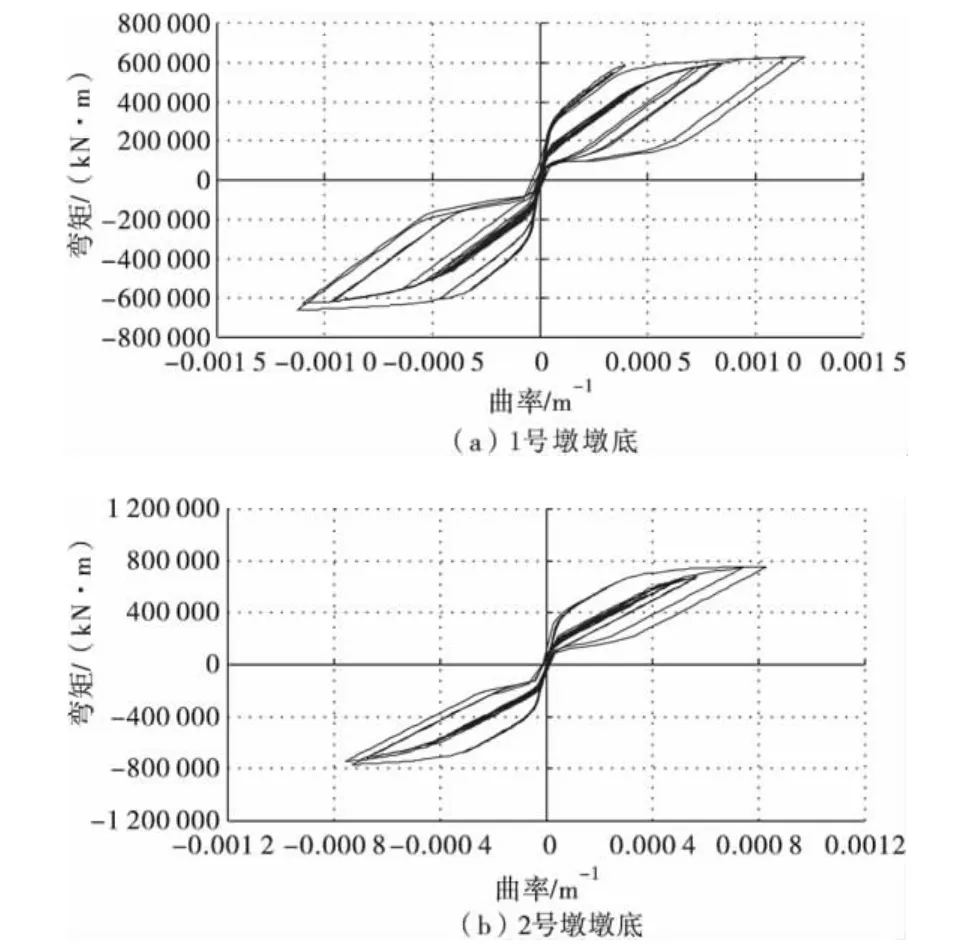
图9 W3作用下墩底弯矩－曲率滞回曲线Fig.9 Moment-curvature hysteresis loop at bottom of piers under W3

3.4 轴压比对桥墩滞回性能的影响

高墩连续刚构桥由于上部结构和墩身自重大，且常采用薄壁空心墩，桥墩轴压比较大，如本文桥墩的恒载轴压比接近0.22。以下分析高轴压比对桥梁的地震响应的影响。

为了分析轴压比对桥墩地震响应的影响，计算了在 W3 作用下，轴压比分别为0.22，0.132 和0.066时桥墩的地震响应。图10为1号墩墩底的弯矩－曲率滞回曲线。

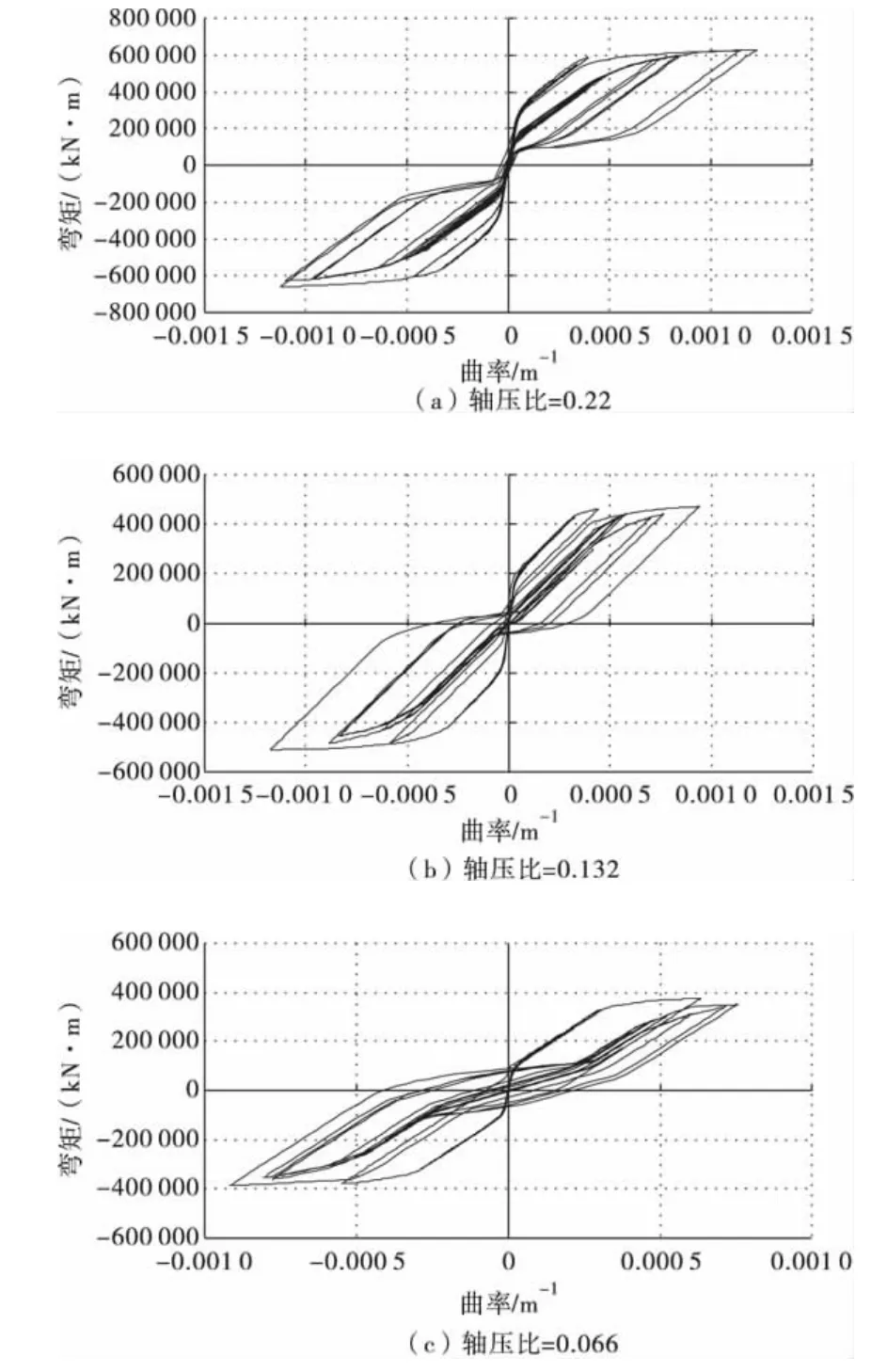
图10 不同轴压比下1号墩墩底弯矩－曲率滞回曲线Fig.10 Moment-curvature hysteresis loop at the bottom of No.1 pier under different axial compression ratios

从图10的墩底截面弯矩－曲率滞回曲线可以发现，在高轴压比下，弯矩－曲率滞回曲线具有明显的捏拢现象，随着轴压比的减小，滞回曲线的捏拢现象减弱。

表6为1号桥墩时程响应最大值。从表6可以得到，轴压比对桥墩墩底内力和墩顶位移影响较大，随着轴压比的减小，墩底内力和墩顶位移随之减小。

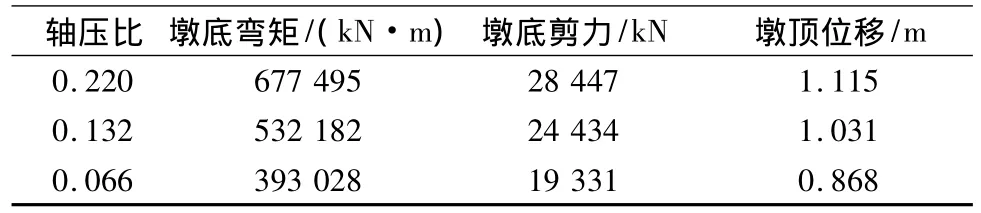
表6 不同轴压比下1号墩最大响应值Table 6 The maximum response of No.1 pier under different axial compression ratios

A.V.Pinto，J.Molina，等［9］曾针对矩形空心墩进行了大比例尺的往复加载试验，当桥墩轴压比为0.1左右时，试验得到的滞回曲线也具有明显的捏拢现象。这表明本文计算得到的弯矩－曲率滞回曲线中的捏拢现象是正确的。

4 结语

以一高墩大跨连续刚构桥为研究对象，对其进行了顺桥向非线性地震响应分析，得出以下结论:

1)连续刚构桥的顺桥向非线性地震反应在中硬场地较中软和软弱场地上的小，因此从有利于抗震的角度考虑，连续刚构桥适宜修建在地质条件较好的地区。

2)当桥墩处于弱非线性状态时(即非线性变形较小)，其位移响应符合等位移原则，而当桥墩处于强非线性状态时，等位移原则不一定成立。

3)对于桥墩高度相差较大的连续刚构桥，由于顺桥向地震作用下各墩墩顶的位移相同，所以在矮墩的墩底塑性铰区，就需要提供更大的转动能力。

4)高墩连续刚构桥轴压比较大，轴力比对桥墩的弯矩－曲率滞回性能影响较大。高轴压比将对弯矩－曲率滞回曲线产生较明显的捏拢现象，并使墩底弯矩、剪力和墩顶位移增大。

［1］范立础.桥梁抗震［M］.上海:同济大学出版社，1997.

［2］李忠献，史志利.行波激励下大跨度连续刚构桥的地震反应分析［J］.地震工程与工程振动，2003，23(2):68 －76.Li Zhongxian，Shi Zhili.Seismic response analysis for long-span continuous rigid-framed bridges under excitation of traveling waves［J］.Earthquake Engineering and Engineering Vibration，2003，23(2):68－76.

［3］陈星烨，唐雪松，赵冰.修改的MPA法用于连续刚构桥的抗震性能分析［J］.振动与冲击，2010，29(12):93 －96.Chen Xingye，Tang Xuesong，Zhao Bing.Antiseismic performance analysis of a continuous rigid frame bridge by application of modified MPA method［J］.Journal of Vibration and Shock，2010，29(12):93－96.

［4］夏修身，陈兴冲，王常峰，等.高墩大跨连续刚构桥抗震性能研究［J］.西北地震学报，2010，32(1):88 －91.Xia Xiushen，Chen Xingchong，Wang Changfeng，et al.Study on seismic performance of tall-pier and long-span continuous rigidframe bridge［J］.Northwestern Seismological Journal，2010，32(1):88－91.

［5］刘怀林，郑罡.大跨径连续刚构桥抗震分析及抗震性能评价［J］.公路交通技术，2009(6):81 －84.Liu Huailin，Zheng Gang.Seismic analysis and seismic performance evaluation for large-span continuous rigid frame bridges［J］.Technology of Highway and Transport，2009(6):81 －84.

［6］JTG/T B 02－01—2008公路桥梁抗震设计细则［S］.北京:人民交通出版社，2008.

［7］Computers and Structures Inc..Components＆ Elements of Perform-3D version 4［CP/OL］.California:Computers and Structures Inc.，2006.

［8］Mander J B，Priestley M J N，Park R.Theoretical stress-strain model for confined concrete［J］.Journal of Structural Engineering，1988，114(8):1804 －1826.

［9］Pinto A V，Molina J，Tsionis G.Cyclic tests on large-scale models of existing bridge piers with rectangular hollow cross-section［J］.Earthquake Engineering and Structural Dynamic，2003，32:1995－2012.