桥墩对沱江二维流场影响研究

彭永勤，彭 涛

(1.重庆西南水运工程科学研究所，重庆400016;2.中煤科工集团重庆设计研究院，重庆400016)

跨越河流的桥梁工程主要由于桥墩、桥台对水流的束窄阻水作用，使局部水流流态发生变化，引起相应的河床调整，这种调整主要表现为:在桥墩上游，因桥墩阻水而产生壅水，流速减小，泥沙淤积;在桥墩之间因桥墩束水，水位降低，流速增大，造成局部冲刷［1－5］;在桥位下游，则因水流扩散，流速降低，再一次引起河道的泥沙淤积。同时，由于桥墩的分流和导流作用，可引起水流流向的局部改变，也可能引起主流的摆动和河床的演变。笔者应用流场计算分析软件SMS，利用成渝客运专线沱江吴家坝双线特大桥实测资料对数值模型进行验证，并计算河流流场，分析建桥前后桥墩对河流流场的影响。

1 二维水流数学模型［6－8］

1.1 守恒型浅水方程的基本方程

1.1.1 水流连续方程

1.1.2 X 方向动量方程

1.1.3 Y 方向动量方程

以上各式中:t为时间;x，y为空间坐标;z为水位;h为水深，h=z－zb(zb为河床高程);u，v分别为沿x，y方向的垂线平均流速;g为重力加速度;n为糙率系数;νt为湍流动能扩散系数。

1.2 FVM离散基本方程

本二维水流数学模型采用基于结构网格的有限体积法，变量布置采用部分变量布置在网格节点，部分变量布置在单元质心的方法，在网格的节点布置水位和高程z，zb，在单元的质心布置垂线平均流速u，v。

1.3 连续方程的离散

在以三角形节点为中心，由周围三角形单元的质心和边中心形成的多边形内，对连续方程(1)进行面积积分，具体的积分过程可以离散为:

式中:上标n代表第n个时间步长;Δt代表时间步长;Sj是由通过与zj所在节点相连的三角形中心点所围成的闭合线的面积。

1.4 动量方程的离散

与连续方程离散相似，动量方程在每一个三角形内，对动量方程组(2)、(3)进行面积积分，得到具体的积分过程可以离散为:

式中:i为每个三角形单元的边;¯vn为此边上的法向流速，取相邻两个单元垂线流速的平均。

1.5 计算网格

全长约2.2 km，其中拟建大桥以上1.1 km，拟建大桥以下约1.1 km。

计算区域共划分成2 783个网格，平均网格长度约为25 m，平均网格宽度约为25 m，同时对拟建大桥桥墩附近河段进行了网格加密处理，见图1。

图1 二维数值计算网格Fig.1 Two-dimensional numerical calculation grid graph

2 数学模型验证

模型验证所采用的资料为2009年9月实测工程河段河床地形图和实测水位及流速流向成果(测时流量Q=810 m3/s)。采用实测的表面流速流向资料及水位资料进行验证，验证河槽率定糙率在 0.03左右，岸滩糙率在 0.032 ～0.038 之间。

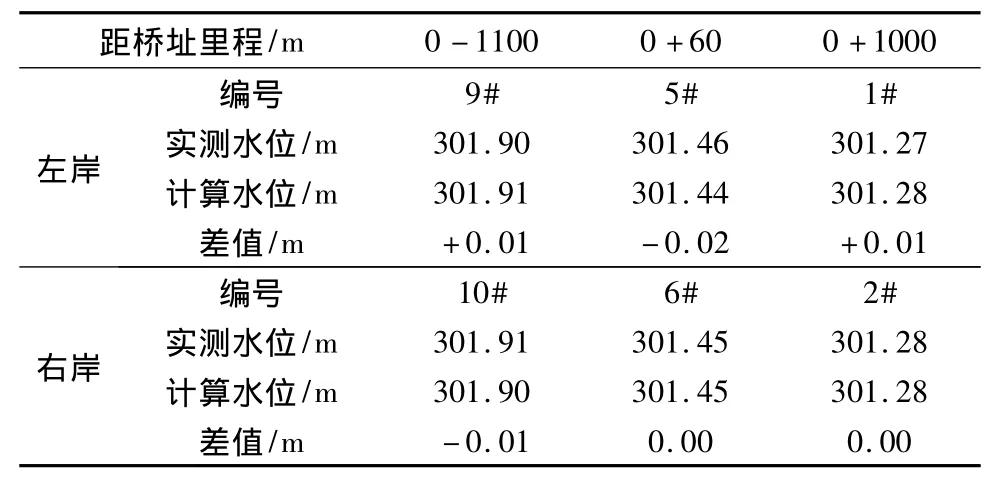
表1 数学模型水位验证(Q=810 m3/s)Table 1 Numerical model level verified table

表2 断面计算流速与实测比较Table 2 Calculated velocity and actual measured of cross-section comparison table

经数模对多个断面复核，计算流量为802m3/s，偏差约8 m3/s，相对误差为1.0%左右。通过工程河段水位、流速分布及流量的验证，证明笔者建立的二维数学模型计算结果与实测资料吻合较好，说明本数学模型的建立和数值计算方法合理，模型基本能够正确模拟工程河段的水流条件变化情况，可以进行下一步工程前后通航水流条件的计算。

3 计算结果分析

拟建吴家坝大桥位于沱江金堂—牛佛航段，按Ⅴ级航道标准论证，设计最高通航水位采用3年一遇洪水标准，流量为6 000 m3/s。根据数模计算结果:建桥前，当流量为两年一遇洪水 Q=4 730 m3/s时，桥轴线处表面流速为1.08 ～2.85 m/s，其流向与桥轴线法向的交角在左1.5～右9.0°之间;当流量为3年一遇洪水Q=6 000 m3/s时，桥轴线处表面流速为1.39～3.40 m/s，其流向与桥轴线法向的交角在左1.4°～右 7.9°。建桥后，当流量Q=4 730 m3/s时，桥位断面的流速在1.18～3.01 m/s之间，最大增加 0.21 m/s，最大减小 0.20 m/s;当流量为3年一遇洪水Q=6 000 m3/s时，桥位断面的流速在1.53～3.51 m/s之间，最大增加0.31 m/s，最大减小0.25 m/s。详见表3，表中夹角为与桥轴线法向的夹角。

表3 流速、流向Table 3 Velocity and flow direction

图2 工程河段建桥前流场Fig.2 Flow field in engineering sections before bridge construction

图3 工程河段建桥后流场Fig.3 Flow field in engineering sections after bridge constrution

从工程前后的流场图(Q=6 000 m3/s)可以看出，桥区河段流场变化主要发生在桥位附近水域，流速有增有减，桥位断面流速增幅最大，增加值在0.2～0.31 m/s，主墩前部和后部流速有一定减小，周边存在一定的绕流流态，但其影响范围有限，其他水域的流速流向较工程前变化不明显，因此大桥建设对通航水流条件影响小。

4 结语

计算结果表明，由于设计方案采用的圆端矩形墩，所以除桥墩附近水域的主流线在建桥前后有一定改变外，其余水域的主流在建桥前后基本没有变化，流速分布及形态一致，其影响范围有限，因此大桥建设对通航水流条件影响小。

［1］高东光.公路与桥梁水毁防治技术［M］.北京:人民交通出版社，2002.

［2］蒋焕章.公路水文勘测设计与水毁防治［M］.北京:人民交通出版社，2002.

［3］Antonis C，Fotis S，Terry W S.Coherent structures in flat-bed abutment flow:computational fluid dynamics simulations and experiments［J］.Journal of Hydraulic Engineering，2003，129(3):171－182.

［4］Briaud J L，Hen H C，Wang J.Pier and Contraction Scour in Cohesive Soils［R］.Washington D.C.:Transportation Research Board，2004.

［5］Tarek S M，Jasim I，Chaudhry H M.Numerical modeling of threedimensional flow field around circular piers［J］.Journal of Hydraulic Engineering，2004，130(2):102 －117.

［6］Arved Js，Raudkivi，Ettema1 R.Clear water scour at cylindrical piers［J］.Journal of Hydraulic Engineering，1983，109(3):338－3491.

［7］Johnson P A，Jones J S.Merging laboratory and field data in bridge scour［J］.Journal of Hydraulic Engineering，1992，119(10):1176－1181.

［8］Melville B W，Sutherland A J.Design method for local scour at bridge piers［J］.Journal of Hydraulic Engineering，1988，114(10):1210－1226.