基于断裂力学原理的石拱桥裂缝允许灌浆压力研究

蒋晓源，宁金成，赵亚飞，周建庭

(1.重庆交通大学 土木建筑学院，重庆400074;2.河南交通职业技术学院，河南郑州450005;3.广西交通科学研究院，广西南宁530007)

在上世纪六七十年代，我国修建了大量的石拱桥，经过多年的运营，或多或少都出现了病害，其中以裂缝最为常见，包括拱腹的纵向裂缝、侧墙的竖向裂缝等等。这些裂缝的产生大大削弱了桥梁结构的整体性，威胁着桥梁的安全运营，迫切需要对全桥裂缝进行有效的修补处理。

目前，压力灌浆是裂缝修补最常见也是最行之有效的处理方式，而作为裂缝灌浆的重要设计参数——灌浆压力，它的正确与否直接关系着裂缝灌浆的成败，因为根据断裂力学原理，灌浆压力过大，将会对裂缝面产生劈裂力，使裂缝进一步扩展;而灌浆压力过小又不能达到修补裂缝、补强结构的目的。在工程实践过程中，裂缝灌浆压力多数是通过压水试验、压气试验或施工员的工程经验确定(多数为0.3～0.4 MPa)，很少有人从理论上来研究石拱桥砌石裂缝灌浆压力的的临界安全值。在这样的背景下，笔者基于断裂力学原理，从简单ANSYS断裂模型出发，计算石拱桥砌石裂缝在不同灌浆压力作用下的缝端应力强度因子，再通过裂缝扩展σ0准则工程判据［1］，分析整段灌浆的允许灌浆压力以及不同分段灌浆长度下的允许灌浆压力，为压力灌浆修补裂缝技术提供理论支撑。

1 石拱桥砌石体抗裂韧度

首先假定石拱桥砌石裂缝为理想线弹性体，根据经典断裂力学原理，裂缝的扩展取决于裂缝端部的应力集中程度这一力学状态(即应力强度因子)与材料性质(即材料的抗裂韧性)，而不取决于结构整体应力状态［1］，即当裂缝端部的应力强度因子大于材料的抗裂韧度，裂缝发生扩展现象;当裂缝端部应力强度因子小于材料的抗裂韧度，裂缝稳定。传统断裂力学将裂纹分为3种类型:I型为张开型断裂，II型为滑开型断裂，III型为撕开型断裂。其中，I型断裂裂缝扩展σ0准则工程判据如下:

式中:KΙ为I型裂纹应力强度因子;KIc为材料断裂韧性。

通过查阅大量文献，知材料断裂韧性KIc与裂纹的形状、大小无关，也和外加应力无关，只决定于材料自身特性，是一个反映材料性能的常数［1］。目前，砌石体的断裂韧度测定可通过实验方法或解析法，综合多年试验研究成果，石拱桥砌石体断裂韧度KIc的数值大约在 0.2 ～0.5 MPa·m－1/2之间［2－5］。

2 简单裂缝在均匀压力作用下缝端应力强度因子［1，6］

2.1 无限板缝端应力强度因子

典型的最简单裂缝如图1，在无限板上裂缝整个裂纹面上作用均布压力σ，根据断裂力学原理，缝端应力强度因子为:

式中:σ为作用在缝面上的均匀压应力;a为1/2缝长。

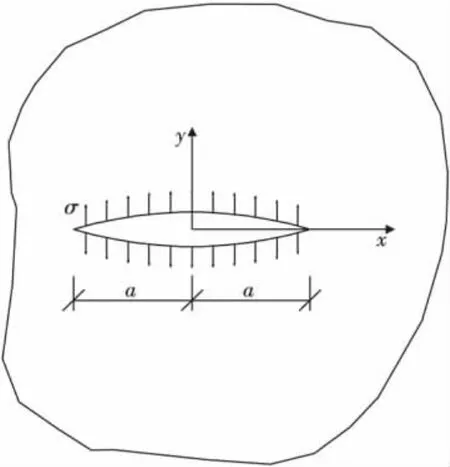
图1 无限板上对裂纹面作用均布压力σFig.1 Put uniform pressure σ to crack of infinite plate

不同缝长，作用在缝面上不同压力时，缝端应力强度因子值如表1。

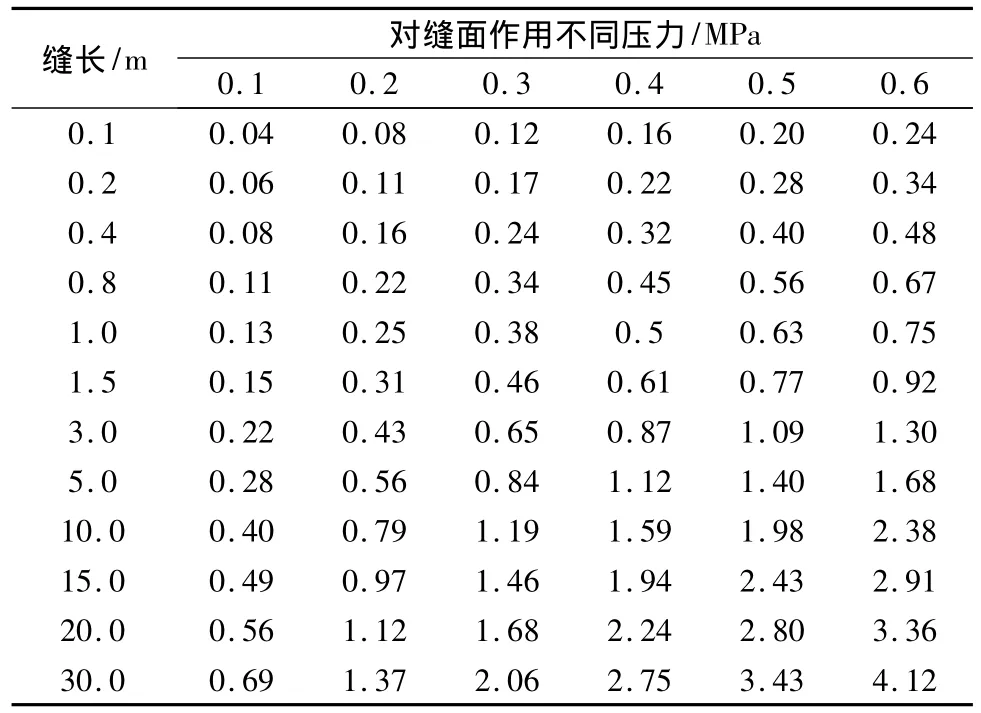
表1 无限板不同缝长、缝面作用不同压力的应力强度因子Table 1 The stress intensity factor of infinite plate with different crack length and surface pressure/(MPa·m －1/2)

从表1可以看出，对缝面作用相同压力时，随着缝长的增长，缝端应力强度因子不断增大;当缝长一定时，随着对缝面作用压力不断增大时，应力强度因子也呈递增趋势。

2.2 有限板缝端应力强度因子

对于有限板上裂缝(图2)，缝端应力强度因子为:

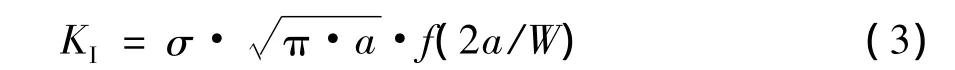
式中:σ为作用在缝面上的均匀压应力;a为1/2缝长;W为与裂缝走向一致的板边长度;f(2a/W)为考虑有限板两侧由于解除了位移约束而使裂纹端部应力强度因子提高的修正系数，部分具体取值见表2。

表2 不同的2a/W值下函数f(2a/W)的值Table 2 The f(2a/W)value under different 2a/W values

由表2可以看出，2a与W越相近时，f(2a/W)值越大，且始终是f(2a/W)≥1的值，即是说在相同缝长、缝面作用相同压力下，由于板两边的自由边界的影响，有限板裂缝应力强度因子始终比无限板应力强度因子大。

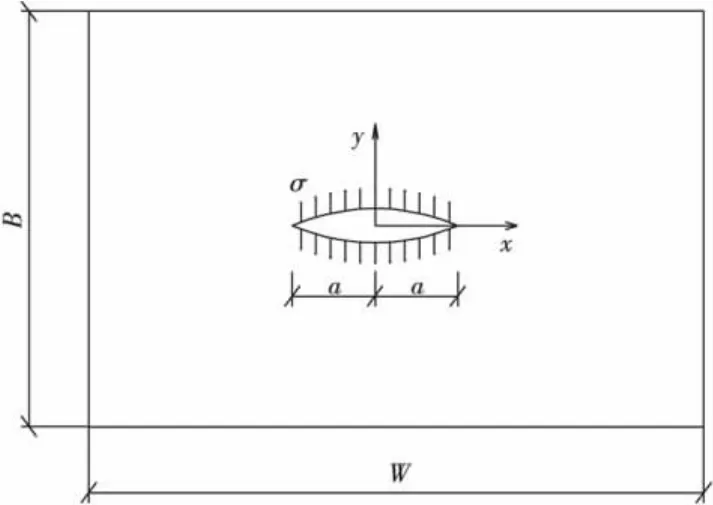
图2 有限板上对裂纹面作用均布压力σFig.2 Put uniform pressure σ to crack of finite plate

3 砌石裂缝允许灌浆压力

3.1 整段灌浆方式

假设结构形式简单、裂缝形态规则，砌石裂缝在灌浆压力作用下为I型裂缝，故整段允许灌浆压力可以直接用断裂力学原理的公式(2)、公式(3)近似计算不同灌浆压力、不同缝长时的缝端应力强度因子，或在已知石拱桥砌石体抗裂韧度条件下计算允许灌浆压力(注:假设竖向裂缝不受灌浆材料自重的影响)。

假设 KIc=0.2，0.3，0.4，0.5 MPa·m－1/2，取W=20m，B=10m，不同缝长下理论允许灌浆压力见表3，允许的灌浆压力与缝长关系曲线见图3。

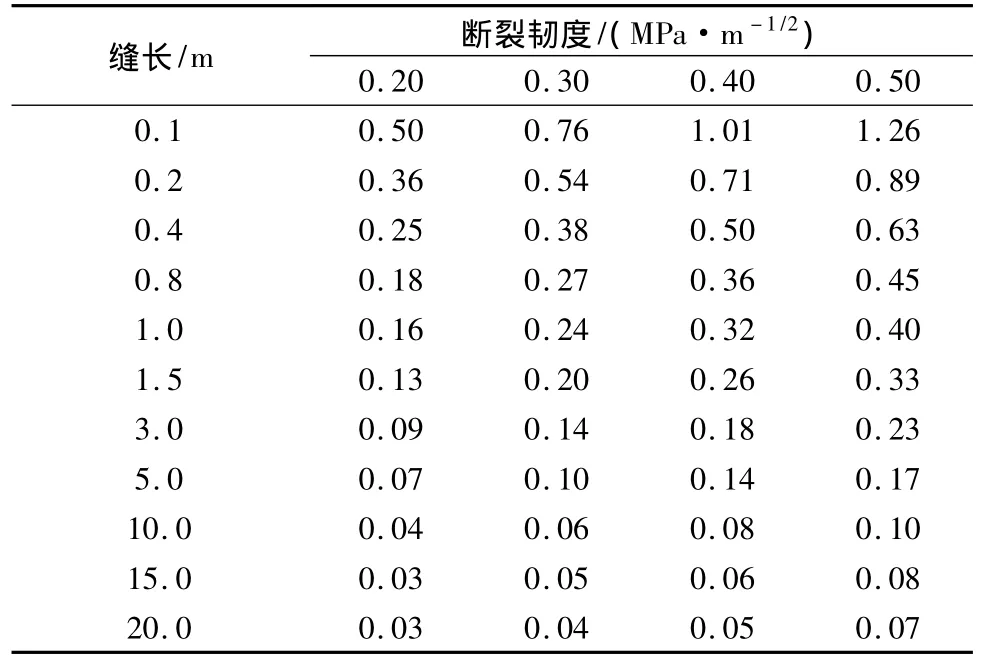
表3 允许灌浆压力Table 3 Allows grouting pressure /MPa

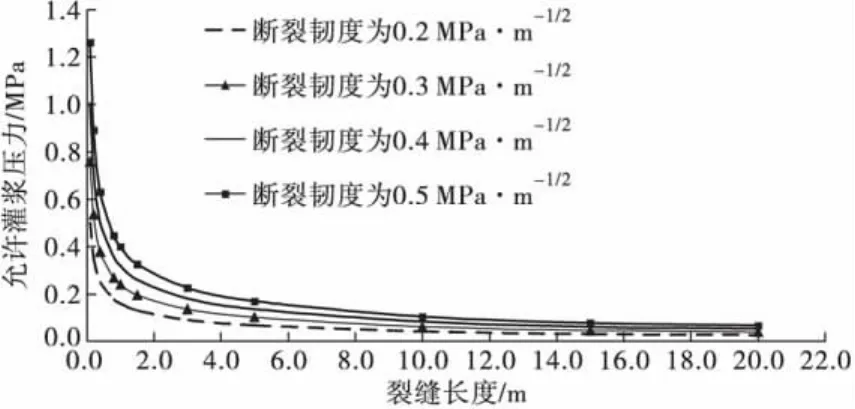
图3 允许的灌浆压力与缝长关系曲线Fig.3 Allowable grouting pressure and the crack length relationship curve

从图3可以看出，在已知材料断裂韧度的前提下，随着缝长不断增长，裂缝允许灌浆压力呈不断下降趋势(其中，裂缝为0～2 m长度时下降最为急剧)。这严重威胁着灌浆质量的保证，故须提高灌浆压力，对长裂缝宜采用分段灌浆裂缝方式。

3.2 分段灌浆方式

当缝长较长时，宜采用分段灌浆的方式。灌浆多数采用环氧砂浆对裂缝进行封闭，对要设进浆孔与出气孔的位置进行预留，逐个对注浆孔进行注浆，当相邻出浆孔流出浆液与注入浆液浓度一致时，换至下一个注浆孔。这种注浆方式使作用在缝面上的压力分布大致呈均匀分布形式。由于这种灌浆方式的优越性，在实际工程中得到了广泛的运用。但是分段灌浆如何分段，分段长度多少为宜，目前一般都是经验取值，还缺乏在理论上论证。

分段灌浆方式计算裂缝允许灌浆压力同整段灌浆方式一致，对于结构形式简单且裂缝形态规则时裂缝允许灌浆压力可以采用理论近似求解，但当裂缝形态不规则时，就需要采用数值解法来求解，当前工程中广泛采用的数值解法是有限单元法。

4 工程实例

4.1 问题描述

以某石拱桥主拱圈拱腹面作为研究对象，建立一个简单的ANSYS二维断裂模型。拱腹横向宽B=12 m，纵向长W=16 m，有一条长为12 m的纵向砌石裂缝，拱桥砌石体的弹性模量为5 650 MPa，泊松比为0.2，对裂缝作用不同的均布拉应力值σ。

4.2 有限元模型建立［7－9］

利用对称条件，取计算模型的1/4建模，以缝尖端为坐标原点，x方向与裂缝平行，y方向与裂缝垂直。单元采用Plane 82(图4)，8个节点，每个节点有2个自由度，四边形和三角形混合网格。由于裂缝尖端存在应力奇异性，利用ANSYS里的KSCON命令来使裂缝尖端生成奇异单元来模拟，之后进行网格划分。对1/4模型的左右侧面和下侧面(裂缝处除外)进行SYMM约束处理，最后对模型的上侧施加σ的均布拉应力，1/4网格划分模型图如图5。

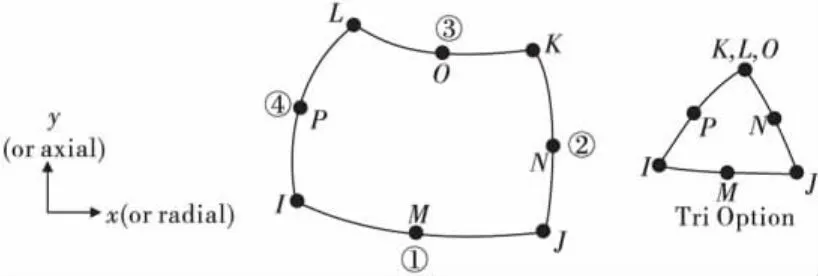
图4 Plane 82几何单元Fig.4 Geometric units of Plane 82

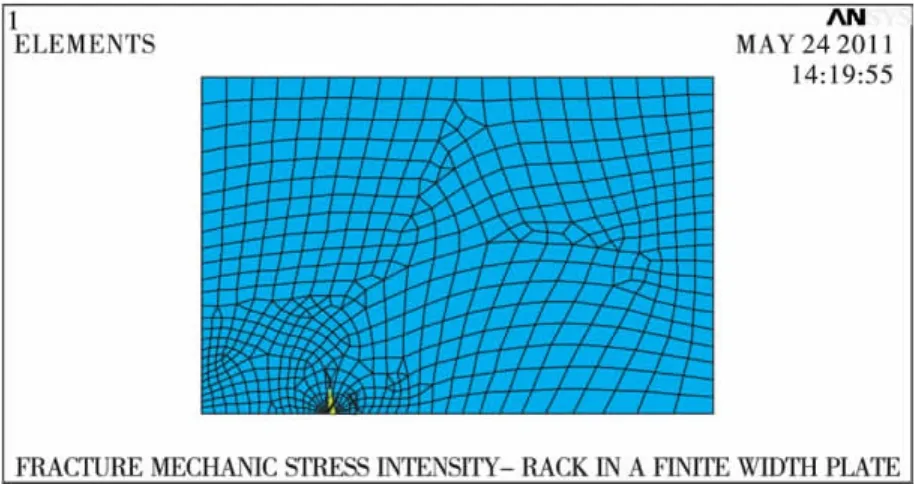
图5 1/4网格划分模型Fig.5 1/4 Mesh model diagram

4.3 缝端应力强度因子求解过程

依次选取1，2，3节点定义路径(图6)，其中1点必须在缝尖端上，然后采用J积分方法求解缝端应力强度因子。J积分是通过定义单元应变能及在积分路径上应力应变位移回路围线上积分来求解。求出J积分后，利用J积分与应力强度因子之间的关系式(4)［1，9］，换算得到缝端的应力强度因子值。

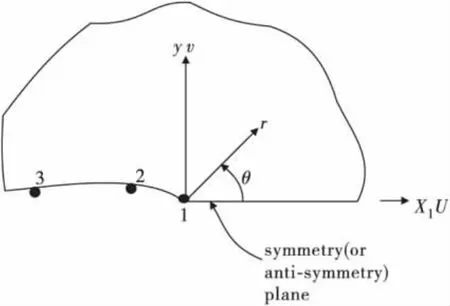
图6 路径定义Fig.6 Definition sketch of the path

4.4 结果分析

对不同分段灌浆长度，采用J积分方法计算的缝端应力强度因子值见表4，应力强度因子与灌浆压力关系见图7。

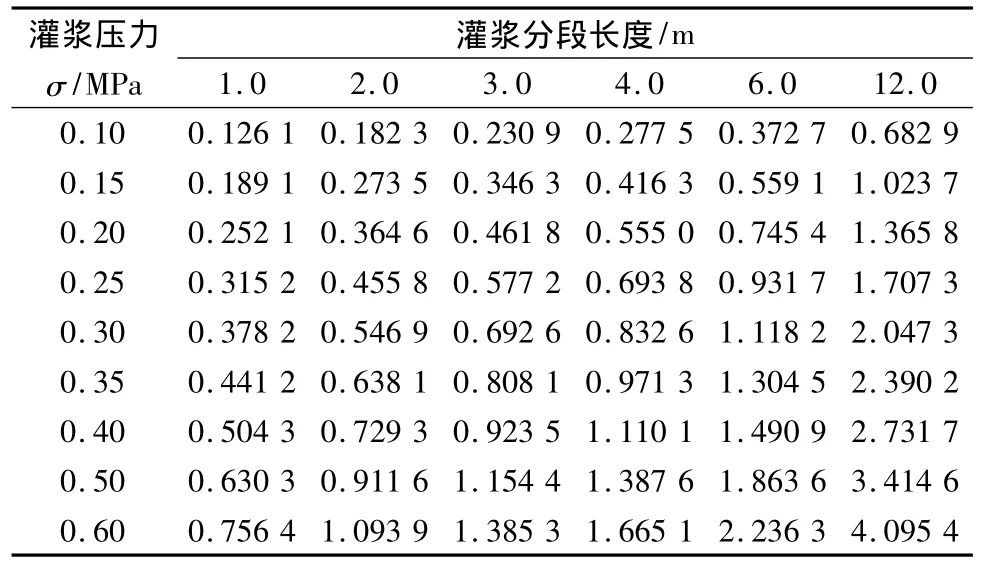
表4 缝端应力强度因子汇总Table 4 Summary of slit tip stress intensity factors/(MPa·m －1/2)

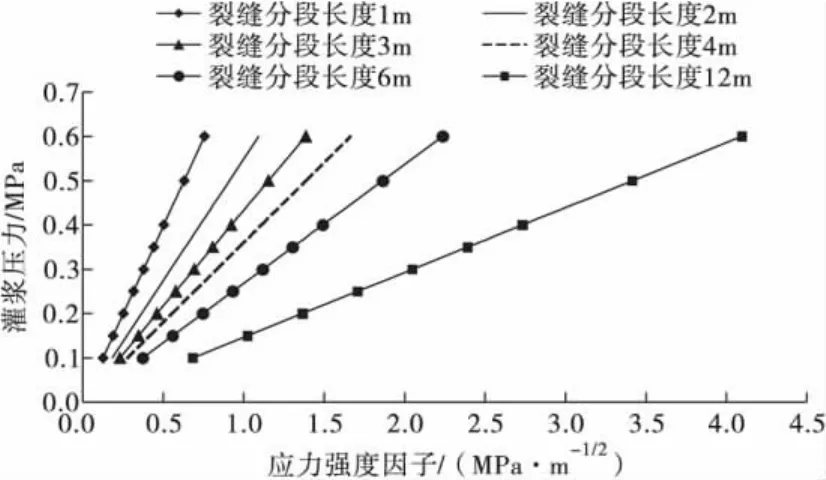
图7 裂缝在各分段灌浆长度下的允许灌浆压力Fig.7 Allow grouting pressure of crack in each segment length

从计算分析结果可以看出，石拱桥砌石裂缝灌浆分段长度越长，允许的灌浆压力越低，即分段长度与允许的灌浆压力成反比。例如石拱桥砌石体断裂韧度取0.5 MPa·m－1/2时，根据断裂力学裂缝 σ0扩展判据，即材料能承受缝端最大应力强度因子为0.5 MPa·m－1/2，采用1 m 一段进行压力灌浆，允许灌浆压力最大可用0.35 MPa，采用3 m一段进行压力灌浆，允许灌浆压力最大可用0.2 MPa;采用6 m整段进行压力灌浆，允许灌浆压力最大可用0.1 MPa;采用12 m整段进行压力灌浆时，不能满足砌石体的防裂要求。

5 结论

1)根据理论计算和有限元数值结果分析，当石拱桥灌缝长度达到一定长度时，只需在缝面上作用少许灌浆压力就会使缝端的应力强度因子超过砌石体的断裂韧度，从而引起裂纹扩展;

2)保证灌浆质量和防止裂缝扩展是一对矛盾体，想要解决矛盾，必须得对裂缝进行分段灌浆，以提高允许灌浆压力值来保证灌浆质量;

3)根据石拱桥砌石体断裂韧度低的特性，裂缝灌浆压力宜采用低压分段灌浆法;

4)分段太短势必也增大工作量，降低工作效率，故须严格论证，兼顾三者，即提高工作效率，又在保证灌浆质量的同时，防止裂缝劈裂扩展。

［1］洪起超.工程断裂力学基础［M］.上海:上海交通大学出版社，1987.

［2］于骁中.岩石和混凝土断裂力学［M］.长沙:中南工业大学出版社，1991.

［3］肖小松，王根生.断裂力学与砌体强度设计［J］.四川建筑科学研究，1997(3):2－6.Xiao Xiaosong，Wang Gensheng.The fracture mechanics and strength of masonry design［J］.Sichuan Building Research，1997(3):2－6.

［4］梁汝涛，乔纪中，赵森，等.砌石体的断裂韧度［J］.砌石坝技术，1987(1):51－56.Liang Rutao，Qiao Jizhong，Zhao Sen，et al.Masonry body fracture toughness［J］.Stone Masonry Dam Technology，1987(1):51 －56.

［5］李妍，孟广伟，尹新生.砌体等效断裂韧度的实用解析方法研究［J］.西安建筑科技大学学报，2009，41(6):800 －888.Li Yan，Meng Guangwei，Yin Xinsheng.The masonry of equivalent fracture toughness of a practical analytical method［J］.Journal of Xi’an University of Architecture and Technology，2009，41(6):800－888.

［6］张国新，李海枫.用断裂力学研究混凝土裂缝的允许灌浆压力［J］.水利水电技术，2009，40(12):52 －55.Zhang Guoxin，Li Haifeng.Using fracture mechanics study on the allowable grouting pressure of concrete crack［J］.Water Resources and Hydropower Engineering，2009，40(12):52 －55.

［7］朱伯芳.有限单元法原理与应用［M］.北京:中国水利水电出版社，2004.

［8］赵海涛，战玉宝，杨永腾.基于ANSYS的应力强度因子计算［J］.煤矿机械，2007(2):22 －23.Zhao Haitao，Zhan Yubao，Yang Yongteng.ANSYS based on the calculation of stress intensity factor［J］.Coal Mine Machinery，2007(2):22－23.

［9］赵伟，向阳开.三点弯曲梁裂缝应力强度因子有限元分析［J］.重庆交通大学学报:自然科学版，2007，26(增刊1):1－2.Zhao Wei，Xiang Yangkai.Three point bending beam crack stress intensity factor of the finite element analysis［J］.Journal of ChongqingJiaotong University:NaturalScience， 2007， 26(supp1):1－2.