基于行星式旋转机构的恒速控制系统研究

吕科，熊庆宇，石为人

（重庆大学 自动化学院，重庆 400030）

现代光学加工设备与现代光学加工过程密不可分，是实现现代光学加工工艺的关键。为了适应现代光学加工工艺，各种现代光学加工设备不断涌现。光学加工是一个复杂的工艺过程，不仅存在磨盘与工件之间的机械切削，还有研磨液与工件之间的化学作用［1］，精密的光学仪器，更需要纳米级的精度，而且整个加工过程周期长。磨头作为抛光过程中的末端执行器，更是实现抛光工艺效果和抛光效率的保证。目前，大部分磨头以行星轮结构来实现行星运动。这种结构存在公转半径固定，不易调节偏心距，传动比固定，不易调节转速比，机构复杂，体积大等问题。本文针对这些问题，基于研制出的具有双转子行星式旋转机构的抛光磨头，按照抛光过程要求自转轴、公转轴的速度波动小，两轴之间能够实现任意的速比，能够在要求的范围内无级调速等实际需求，设计并研究了基于行星式旋转机构的转速控制系统，包括机构的特性，多模态PID，耦合力矩补偿，位置反馈摩擦力补偿等控制策略。

1 抛光磨头结构

在光学研抛过程中，工件材料去除量、相对压强与相对速度满足Preston方程［2］：

式中：U为单位之间内的材料去除量；A为工艺系数，与工件材料、磨盘、抛光剂有关；p为工件与磨盘之间的相对压强；v为工件与磨盘之间的相对速度。

在计算机控制下，磨头以特定的速度、压强及路径在工件表面运行，通过控制每一区域的驻留时间，即可精确地控制表面材料去除量，达到修正误差，提高精度的目的［3］。

抛光磨头采用行星式旋转运动方式。其结构示意图及基本结构如图1所示。

图1 磨头结构示意图Fig.1 Polishing head schematic

通过自转和公转电机实现转速比的任意可调性；通过自制偏心轴螺杆调距机构实现0～0.5倍抛光盘直径大小偏心距的大范围调节；在自转轴内布置气压系统，以获得可调且稳定输出的抛光压力；活塞杆（轴）与自转轴之间有轮齿等传动连接，抛光盘和活塞杆（轴）采用球铰链联结，以增强抛光盘对工件面形变化的自适应性。

基于行星式旋转机构的特点，采用控制器＋驱动器＋伺服电机的模式，作为双转子转速控制系统，如图2所示。

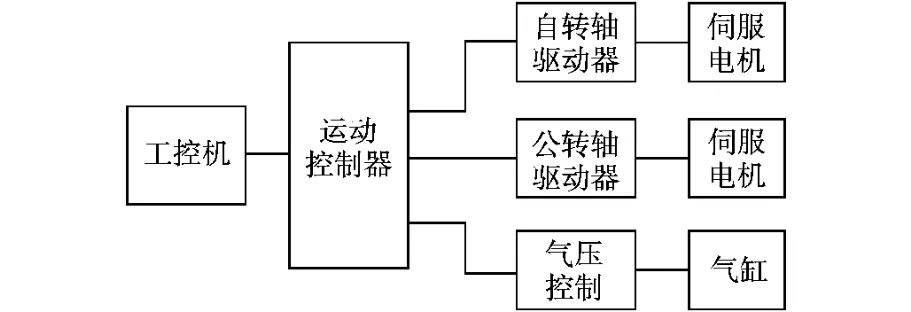
图2 磨头控制示意图Fig.2 Scheme of polishing head control system

2 双转子转速控制系统设计

此系统采用交流永磁同步伺服电机作为自转轴及公转轴的执行器，通过控制两个电机的转速来达到抛光过程中对速度的要求。

2.1 行星式旋转机构的扰动特性

在研抛过程中要求双转子速度在一定范围内连续可变，但在调速完成后，又要求较高的转速稳定性。对于这种二自由度的旋转机构，其机构框架的质量分布，加工精度不对称性，旋转时都会产生扰动转矩。

在无负载情况下，通过实验测得双转子具有周期性扰动，以自转轴为例，如图3所示。

双转子在研抛过程中，具有耦合性。磨盘与工件的接触面上的合速度由自转轴的速度和公转轴的速度组成。因此受到的阻力虽然和速度相反，但可以分成两个阻力，即自转运动产生的阻力和公转运动产生的阻力。

图3 自转轴周期性扰动Fig.3 Periodic disturbance of rotation

为建立阻力距方程，假设工件上的压力是均匀分布的，研磨系数为μ。磨盘转速恒定为ω，磨盘半径为R1，O1，O2分别为公转和自转的原点。A点位工件上某点受力。如图4所示。

图4 磨盘与工件相对运动关系Fig.4 Relation of movement between plant and workpiece

公转轴固定，自转轴以ω2的角速度运行，则自转阻力矩为

当公转运动时，由于磨盘同一环带上的速度不同，从而产生不同的粘滞阻力，作用于自转轴上就形成了阻力矩。

分析磨盘A点上的受力为

式中：ds为点的微元面积。

整个接触面上的摩擦力对O2点产生的力矩为

其中

公转时，自转轴受到的阻力矩是一个与磨盘半径，偏心距有关的函数，当e较大，磨盘半径一定时，阻力矩较小，当e一定，R1较大时，阻力矩较大。

公转受到的阻力矩为

1）当e＝R1时，

2）当0＜e＜R1时，

3）当e＝0时，

由此，双转子在研抛过程中的耦合性，可以解耦为自转轴自转时的阻力矩和公转轴作用于自转轴的阻力矩，从而可以在控制器中加入阻力矩补偿。

2.2 双轴永磁同步电机模型建立

交流永磁同步伺服电机的状态方程［4］：

式中：R为绕组等效电阻；L为等效电感；p为电机极对数；ωm为转子机械角速度；Ψr为每对磁极磁通；id为d轴电流；iq为q轴电流。

本系统的转速执行器主要有2个松下A5的电机构成，双转子基本参数为：额定输出功率2 kW，额定转矩9.55N·m，瞬时最大转矩28.6 N·m，额定电流11.6A，额定转速2000r／min，最高转速3000r／min，增量式编码器每转1048576个脉冲，自转轴4∶1，折合惯量6.5×10－4kg·m2，公转轴10∶1，折合惯量2.45×10－3kg·m2。

双轴伺服系统传递函数如图5所示。

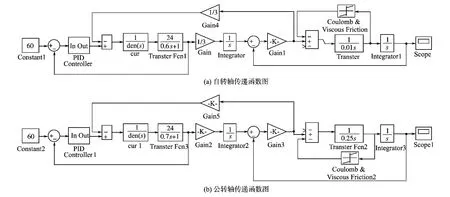
图5 双轴伺服系统传递函数Fig.5 2－axis servo system transfer function

在实际场合下，工业驱动电机的转矩响应应与一阶惯性环节近似。通过实验数据获取速度响应曲线，如图6所示。

图6 速度响应曲线Fig.6 Rotate speed curve of 100r／min

简化转轴传动部分传递函数为

式中：τa，τb为响应延迟时间。

2.3 双转子转速控制器设计

控制对象特点为：1）具有周期性大扰动，也具有不确定扰动；2）双转子具有速度耦合性；3）负载可变，粘滞力大；4）公转轴具有较大惯性，较低速度。

基于PID的基础上研究适用于此系统的控制规律。对于有效抑制扰动，在控制系统中加入扰动观测器。如果把干扰观测器加到PI速度控制回路中，则整个系统就变成2自由度控制的鲁棒控制系统，可以分别独立设计［5］。如图7所示。

图7 扰动补偿控制系统Fig.7 Disturbance compensation control system

为了提高控制系统的快速性，稳定性，在复合控制中加入多模态PID控制。将速度偏差分成3档，大，较大，小。当偏差为大时，采用适中比例系数，小积分系数；偏差较小时，采用较大比例系数，较小积分系数；当偏差小时，采用大比例系数，大积分系数，加上微分作用。

由于负载需要变化，即研抛过程中，磨盘的大小需要更换，因此对应不同磨盘，控制器的参数也将发生变化，通过经验值调试不同的磨盘对应的PID参数，建立参数组合，不同的磨盘从组合中选取不同的参数组。

控制系统存在周期性扰动，由旋转特性可知，扰动是一个关于旋转角位置的周期函数。通过测试可以获取扰动关于角位置的函数，在控制器设计时通过位置反馈，补偿扰动转矩，从而达到较好的控制效果。

结合不同控制系统的不同特点及控制对象的特性。设计复合控制系统如图8所示。

图8 双转子复合控制系统Fig.8 Dual－rotor composite control system

3 仿真及实验结果

本文仿真系统在Matlab 7.1中的Simulink环境下进行仿真研究。

双转子控制系统分别采用了PID控制和基于PID的复合控制方法。两种控制器参数的选取都为闭环系统下的性能相对最优。自转轴和公转轴给定速度分别为100r／min和90r／min。系统中分别施加4sin（12t）的正弦扰动信号，噪声为1.5的白噪声信号，1s时突加负载转矩扰动4N·m。

图9、图10、图11分别是不同干扰环境下，常规PID控制与复合控制对不同扰动的抑制情况。

图9 白噪声扰动Fig.9 Disturbance of white noise

图10 负载突变扰动Fig.10 Sudden disturbance of load

图11 正弦波扰动Fig.11 The sin wave disturbance

图12为设定自转轴速度100r／min时，通过松下A5自带的示波器软件，观测的电机阶跃响应曲线。

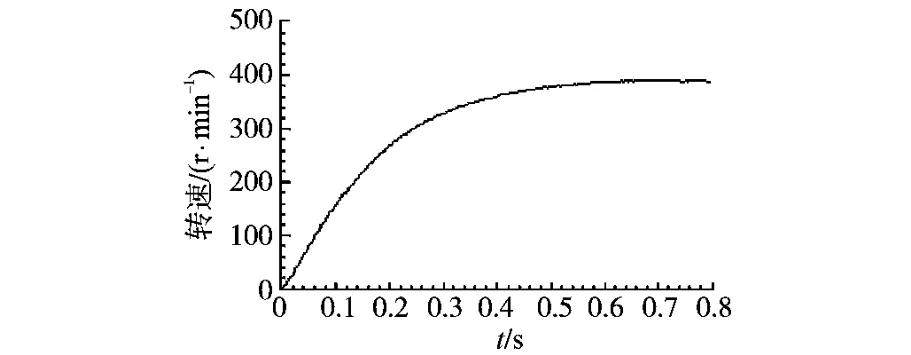
图12 实际自转轴速度控制曲线Fig.12 Real rotation speed curve of control system

4 结论

从仿真结果及实验数据可以看出，双转子行星式旋转结构恒速控制系统，在系统动态运行过程中，系统不可避免地存在非线性和不确定性因素，且旋转机构相互耦合，不同磨盘对应不同的负载情况。研抛过程中工件的曲率不同产生的摩擦力、粘滞力也不同。针对此系统的特性，采用本文提出的控制器、驱动器、伺服电机结合的形式，运用耦和转矩补偿、位置反馈摩擦力前馈补偿的复合控制，系统在不同的扰动下及控制要求下，具有良好的鲁棒性及速度平稳性。

［1］杨力.先进光学制造技术［M］.北京：科学出版社，2001.

［2］Preston F W.The Structure of Abraded Glass Surfaces［J］.Trans.Opt.Soc.，1992，23（3）：141－164.

［3］王贵林.SiC光学材料超精密研抛关键技术研究［D］.长沙：国防科技大学，2002.

［4］尔桂花，窦曰轩.运动控制系统［M］.北京：清华大学出版社，2002.

［5］海老原大树.电动机技术实用手册［M］.王益全，刘军，秦晓平，等译.北京：科学出版社，2005.

［6］Kurfess T R，Whitney D E.Predictive Control of a Robotic Grinding System［J］.Journal of Engineering for Industry，1992，114（4）：412－420.

［7］Kamijyo K，Sakamoto M，Asao T，et al.Development of an Automatic Polishing System for Metal Molds Anddies［J］.JSME（C），1989，55（2）：193－196.

［8］杨上陆，董湘怀.基于PMAC和松下伺服电机的电子横移控制系统研究［J］.机床与液压，2004（11）：73－76.

［9］陈诚，李世华，田玉平.永磁同步电机调速系统的自抗扰控制［J］.电气传动，2005，35（9）：13－16.