新型矩阵式MMC拓扑结构及控制算法研究

方璇，李永东，许烈，王奎

（1.金华市电业局，浙江 金华 321000；

2.清华大学 电力系统国家重点实验室，北京100084）

1 引言

高压大容量变频调速领域中，比起矩阵变换器，基于H桥级联型的多电平变换器更具有优势，但也存在一些问题，如每个功率单元前端采用二极管不控整流，所以在电机制动时不能实现能量回馈电网，另外就是网侧必须有移相变压器接入，移相变压器的抽头多、体积大，成本也很高。为此，很多学者提出了改进的拓扑结构［1－2］，随着模块化多电平（MMC）拓扑的提出，采用模块化多电平拓扑与矩阵变换器结构相结合是一种可行的方案［3－4］。它秉承了矩阵变换器和 MMC的优点，不仅可以升降压，而且还能通过增加H桥级联数，提高电压等级。然而其控制方法还不成熟，美国学者为此提出了该拓扑两电平的控制方案［5］，其中心思想是采用空间矢量PWM控制，由于开关状态繁多，使得其控制变得复杂，而且也不易于扩展到多电平。本文在此基础上，将其基本拓扑进行改进，并扩展到多级H桥级联结构，提出了载波层叠PWM调制方法和悬浮电容电压平衡方案。不仅大大增加了电平数和提高电压等级，而且还简化了控制的复杂程度。最后，在Matlab中搭建了一个8级H桥级联的矩阵式MMC变换器，仿真结果证明了改进的新型矩阵式MMC拓扑结构和相应控制方案的正确性。

2 新型矩阵式MMC建模

一个8级H桥级联的新型矩阵式MMC结构如图1所示，其结构类似于矩阵变换器，输入为三相交流电源，输出为三相交流负载，不同的是，其两端均通过电感元件相连。它由9个结构完全相同的桥臂组成。每个桥臂都相当于一个受控电压源，包含8个H桥单元。本文在此基础上在每个桥臂中添加了一个滤波电感。当该拓扑结构正常运行时，每个桥臂均同时接入，参与合成交流输出。

图1 改进的矩阵式MMC拓扑Fig.1 Improved matrix MMC topology

假设输入的三相交流电压瞬时值为VA，VB，VC，输出电压瞬时值为VU，VV，VW。每个桥臂的电压瞬时值可表示为

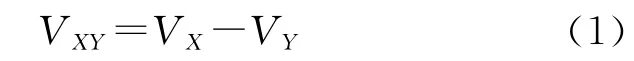
式中：x＝A，B，C；y＝U，V，W。

同理，假设每相桥臂的电流分别为：iAU，iBU，iCU，iAV，iBV，iCV，iAW，iBW，iCW，输出电流分别 为iU，iV，iW，则：

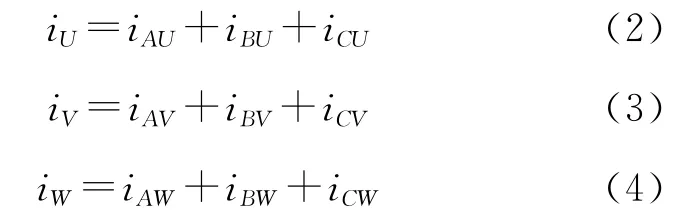
由式（1）～式（4）可知，矩阵式 MMC的电压电流输入输出关系。

如图1所示，在一个开关周期内，令S为开关状态，ta为PWM信号占空比，每个H桥单元的开关状态可分为4种。

1）充电状态S＝1。①Q1和Q4导通。电容正极接到X端，负极接到Y端。当电流从X流向Y端，D1和D4导通，电容充电。②Q2和Q3导通。电容正极接到Y端，负极接到X端。当电流从Y流向X，D2和D3导通，电容充电。

2）放电状态S＝－1。①Q1和Q4导通。电容正极接到X端，负极接到Y端。当电流从Y流向X，Q1和Q4导通，电容放电。②Q2和Q3导通。电容正极接到Y端，负极接到X端。当电流从X流向Y端，Q2和Q3导通，电容放电。

3）PWM状态S＝ta。即半充电或半放电状态。

4）旁路状态S＝0。Q1和Q2同时导通，或者Q3和Q4导通，构成共发射极连接或共集电极连接的双向开关，从而令X和Y端短接，即旁路状态。见表1。

表1 悬浮电容状态Tab.1 Suspended capacitance state

由于每个H桥单元中含续流二极管，所以它没有断开状态。

3 PWM调制及悬浮电容电压平衡控制

对以上矩阵式MMC拓扑的控制包括以下2个方面：1）输入交流，合成交流输出；2）控制每个H桥单元悬浮电容电压的平衡。

PWM调制法通常可分为载波层叠法、载波移相法和空间矢量PWM（SVPWM）法等。文献［5］中采用了SVPWM法，由于矩阵式 MMC的开关状态繁多，而当级联数增加时，基本矢量和冗余开关状态的选择会变得更加复杂。而如果采用载波移相PWM，控制电容电压平衡时则需要根据每个单元的电压大小由独立的PI调节器生成不同的参考波，控制器的设计和PWM信号的生成都比较复杂［6］。

通过对矩阵式MMC拓扑的改进后，本文采用了载波同相层叠法，其原理是，针对1个x电平的变换器，采用x－1个等幅值、同频率、同相位的三角波为载波，上下连续层叠，与同一调制波进行比较，在采样时刻根据调制波与各个三角波的比较结果输出不同的电平，并决定对应开关管的开关状态［7］。图2所示为1个5电平载波层叠法的示意图。

图2 5电平调制示意图Fig.2 Five level modulation schematic

每个H桥单元都需一路独立的PWM信号。本文中，调制波是通过输入输出电压的差值给定的，即每个桥臂的电压定为调制波，见式（1）。以桥臂AU为例，假定输出电压给定为VU＝m×Vmsin（ωt），则调制波为

式中：m为调制比；Vm为输出电压幅值；ω为角频率。

假设每个桥臂有n个H桥级联，且每个悬浮电容电压为UC，则－｜n×UC｜≤VAU≤｜n×UC｜。采用载波层叠的PWM调制方法，将VAU与2n个幅值为UC的三角波比较，可得到2n＋1个工作模式，即2n＋1个电平输出。例如，图1中每个桥臂有8个H桥级联，则每个桥臂电压满足－8UC≤Vxy≤8UC，将Vxy与16个幅值为UC的三角波比较，可以得到17电平的桥臂电压输出，同时，由式（5）也可以得到17电平的输出相电压。

而对于任意输出电平电压的输出UON，－｜n×UC｜≤UON≤｜n×UC｜，满足：

式中：SM为每个H桥单元的开关函数。

由式（6）可以看出，对于每个桥臂任意电平的输出，只要满足桥臂中每个H桥单元的开关函数之和等于要输出的电平即可。

对MMC电容电压平衡控制的基本思路是：首先，通过实时检测9个桥臂中每个H桥单元电容的电压大小和输入输出电压电流方向，来确定每个桥臂中每个H桥单元的电容充放电状态。然后，将MMC每个桥臂的H桥单元的电容电压从低到高进行排序，电容电压最高的和最低的进行电容电压平衡控制，即在一个开关周期内，使得电压最高的电容放电，电压最低的进行充电，而电压居中的几个单元进行PWM以合成输出电压。该方法牺牲了一个调制深度，而当H桥级联数越多时，其影响会越小。

设TA＝VAU／UC，ta为PWM 信号的占空比，表2为当检测到桥臂的电压电流均大于0时，其中一个桥臂的8个悬浮电容电压控制方案详解。

例如，图1中，假设检测到桥臂AU输入电压瞬时值为1 000V，输出电压瞬时值为600V，并且电流从输入侧流向输出侧，每个悬浮电容电压设定值为500V。那么，如果要控制一个8级级联的矩阵式MMC悬浮电容电压平衡，首先要检测输入输出电压电流大小和方向，判断每个桥臂H桥单元的悬浮电容需要充电。然后，将每个桥臂的H桥单元电容电压从低到高排序。在一个开关周期内，选择电容电压最低的单元进行充电，即ta＝1；电容电压最高的放电，即ta＝－1。由于输入输出电压差为400V，VAU＜UC，故选择电压次低电容进行PWM使ta等于TA，即0.8。而其余较高的5个H桥单元旁路，即使得ta＝0。

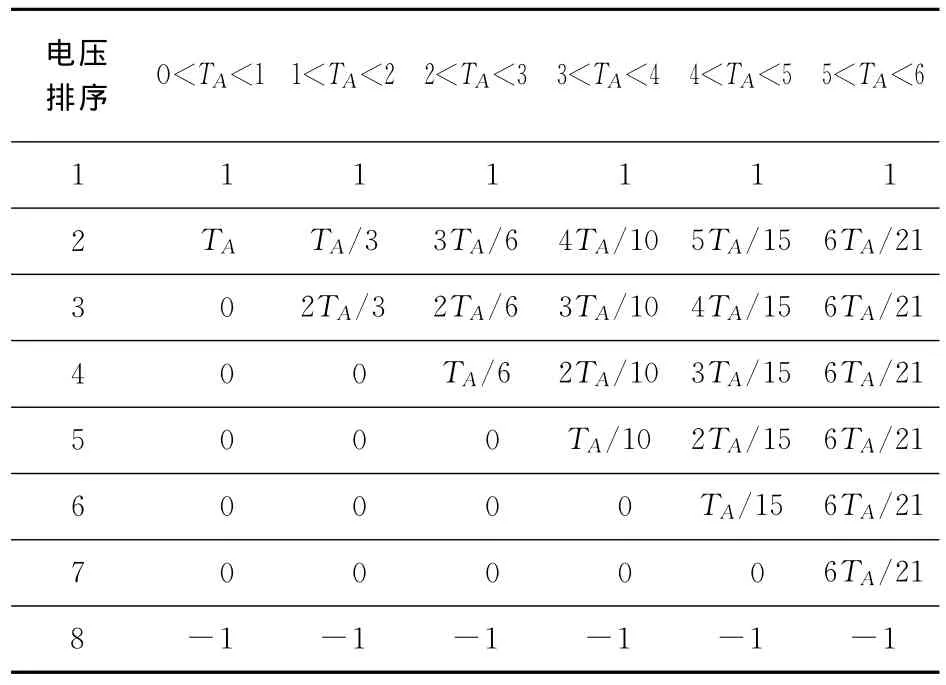
表2 悬浮电容电压控制方案Tab.2 Suspension capacitor voltages control

4 仿真及结果分析

为了验证改进后的矩阵式MMC拓扑结构以及PWM控制算法的正确性，本文在仿真软件包Matlab／Simulink平台上搭建了该拓扑结构的模型并进行了仿真。仿真参数为：输入电压U＝2 000V，悬浮电容电压设定值UC＝600V，输出电压给定值U0＝1 000V，调制比m＝0.9，基波输入频率f0＝50Hz，基波输出频率f＝40Hz，载波频率fs＝5kHz，悬浮电容容量C＝1 000μF，输入侧电感Ln＝1mH，桥臂串联电感Ls＝1mH，桥臂串联电阻Rs＝0.5Ω，负载电阻R＝10Ω，负载电感L＝1mH。

图3～图7为仿真波形，其中，图3a为输入输出端电压电流波形，输入为2 000V的交流电，由上文分析，由于控制算法中牺牲了一个调制深度，故输出相电压应该为13电平的交流电，线电压为25电平。图3a的第3个波形中可以看出输出线电压为25电平，波形较平滑。图3b为其中一个桥臂的8个H桥单元悬浮电容电压的波形，由图3b中可以看出，电容电压基本保持平衡，其正向波动低于50V。图3c为图3b中8个悬浮电容电压的波形细节图，从中可以看出电压平衡控制算法的效果，每次都是电压较低的充电，电压较高的放电，电容电压居中6个单元按大小由低到高进行排序，然后依次给出相应的占空比。

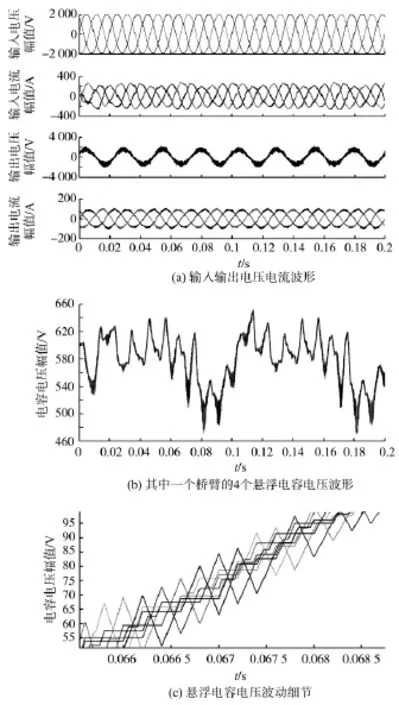
图3 仿真波形Fig.3 Simulalion waveforms

由式（5）可知，改变调制比m，将会对输出电压波形和电容电压波形产生影响，图4为当调制比m＝0.4时的仿真波形图。其中，图4a分别为输入相电压、相电流波形和输出线电压、线电流波形，由图4a中可看出由于减小了调制比，输出线电压变小了，而且电平数也减少到了13电平。图4b为其中一个桥臂的8个H桥单元悬浮电容电压的波形，可以看出，悬浮电容电压正向波动也较小，基本稳定在600V附近。

图5为当输出频率f＝20Hz时，输入输出电压电流波形。从图5a可以看出，频率变小对输入输出电压电流波形影响不大。图5b为其中一个桥臂的悬浮电容电压波形，可以看出，当频率减少时，悬浮电容电压波动变化也不大，基本在允许的范围内。

图4 m＝0.4时的仿真波形Fig.4 Simulation waveforms when m＝0.4

图5 f＝20Hz时的仿真波形Fig.5 Simulation waveforms when f＝20Hz

图6 fc＝2kHz时的仿真波形Fig.6 Simulation waveforms when fc＝2kHz

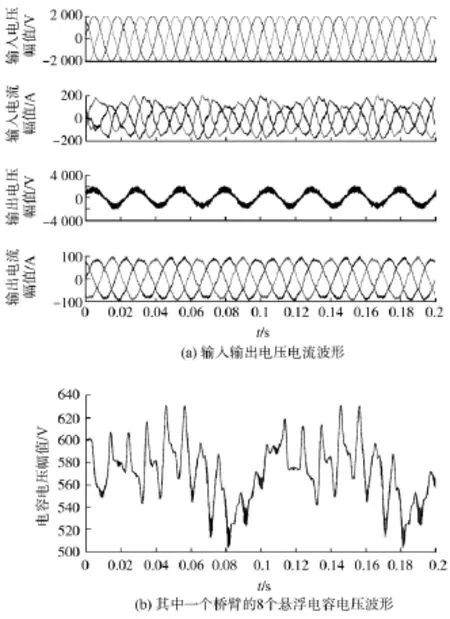
图7 fc＝10kHz时的仿真波形Fig.7 Simulation waveforms when fc＝10kHz

图6为当改变开关频率fc＝2kHz时的波形，图6a为输入输出电压电流波形，可以看出，当开关频率降低，输入电流和输出电流波形有些畸变。图6b为其中一个桥臂的悬浮电容电压波形，可以看出，电容电压波动增大。图7为当开关频率fc＝10kHz时的波形，图7a为输入输出电压电流波形，可以看出，当开关频率增加，输入输出电压电流波形较光滑，毛刺较少，但输入输出电流有些畸变。图7b为其中一个桥臂的悬浮电容电压波形，其波动幅度也有所增加。

5 结论

本文针对矩阵式模块化多电平拓扑进行了改进，并建立了其开关函数模型，提出了一种载波层叠PWM控制策略和电压平衡控制方法，仿真结果验证了控制算法的正确性和可行性。

［1］Peng Fangzheng.A Generalized Multilevel Inverter Topology with Self Voltage Balancing［J］.IEEE Transactions on Industry Applications，2001，37（2）：611－618.

［2］Wang Chenchen，Li Yongdong.A Survey on Topologies of Multilevel Converters and Study of Two Novel Topologies［C］∥IPEMC，2009：860－865.

［3］Martin Glinka，Rainer Marquardt.A New AC／AC Multilevel Converter Family［J］.IEEE Transactions on Industrial Electronics，2005，52（3）：662－669.

［4］Nabae A，Takahashi I，Akagi H.A New Neutral－point－clamped PWM Inverter［J］.IEEE Trans.on Industry Applications，1981，17（5）：518－523.

［5］Angkititrakul，Sitthipong，Ph D.Control and Implementation of a Multilevel Matrix Converter［Z］.DAI－B 67／02，2006：84－117.

［6］李永东，王奎，郑泽东.一种级联型多电平变换器［P］.中国专利：CN101505106，2009－08－12.

［7］李永东，肖曦，高跃.大容量多电平变换器—— 原理·控制·应用［M］.北京：科学出版社，2005.

［8］陈阿莲，何湘宁，吴洪洋，等.基于基本单元串－并（并－串）思想生成多电平变换器拓扑的方法［J］.电工技术学报，2004（2）：41－46.

［9］Lesnicar A，Marquardt R.A New Modular Voltage Source Inverter Topology［C］∥EPE，2003：5.

［10］Marquardt R，Lesnicar A.New Concept for High Voltagemodular Multilevel Converter［C］∥PESC，2004：5.