轴压开口圆柱薄壳屈曲分析与试验

张展智 赵国伟 黄 海 黄承静

(北京航空航天大学 宇航学院，北京100191)

开口圆柱薄壳结构在航空航天以及其他领域中有着广泛的应用，如DODGE卫星的重力梯度杆、Apollo-15中使用的伸展臂、哈勃望远镜的太阳电池帆板支撑杆等，均采用了以开口圆柱薄壳结构为基本构型的伸展机构(STEM，Storable Tubular Extendable Member)［1－3］.在这类应用中，开口圆柱薄壳结构通常只能使用铍青铜材料(QBe2)或碳纤维复合材料(CFRP)，且往往处于两端固支的条件下并需要承受轴向压力的作用，而较大的长径比和径厚比使其容易发生屈曲而导致结构失效，因此，轴压开口圆柱薄壳在两端固支条件下的稳定性是值得工程人员关注的重要问题之一.

针对圆柱壳体受轴压作用时的稳定性，已经形成了诸多理论，如非线性跳跃理论、缺陷理论、初始后屈曲理论、边界层理论等［4－8］.但是，由于开口情况下沿壳体轴向的两条边完全自由，因此很难得到其屈曲载荷的闭合解，这很大程度限制了开口圆柱薄壳的稳定性研究.参考文献［9］最先采用数值方法求解了小挠度假设下的壳体屈曲方程，得到了轴压开口圆柱薄壳的屈曲载荷.此后，文献［10］又采用大挠度假设对该问题进行求解.文献［11］对扇角θ为82°的开口圆柱薄壳进行轴向压缩试验，得到了小挠度假设下的数值解更接近真实屈曲载荷的结论.文献［12］将上述理论方法推广至正交各项异性层合壳，同时考虑了轴向压力、剪力、弯矩的共同作用.文献［13］通过Galerkin方法求解屈曲基本方程，建立了扇角θ≥180°的轴压开口圆柱薄壳的屈曲载荷模型.计算机的发展为求解屈曲问题提供了很大的便利，使得特征值屈曲分析和非线性屈曲分析更加方便快捷，近年来的壳体稳定性研究也开始广泛地借助ANSYS、ABAQUS等商用分析软件，如 Magnucki和Wilde等学者在对三边简支的轴压开口圆柱壳进行屈曲应力计算与数值仿真的过程中即使用了商用有限元分析软件，并得到了可供工程应用参考的结论［14－15］.

本文采用特征值屈曲分析方法来研究各向同性材料的开口圆柱薄壳在两端固支条件下受轴压作用时的稳定性问题，并通过对分析值的拟合给出计算轴压开口圆柱薄壳屈曲载荷的模型，最后采用试验的方法来验证模型的精度.

1 开口圆柱薄壳结构

在空间伸展机构等应用中，开口圆柱薄壳构件往往受到轴向压力P的作用，用来描述开口圆柱壳的几何参数包括长度L、曲率半径R、厚度t、以及扇角θ，如图1所示.

图1 薄壳示意图

应用于空间伸展机构的开口圆柱薄壳结构，其常用的材料包括铍青铜(QBe2)、碳纤维复合材料(CFRP)等.本文仅考虑各向同性材料，因此选择铍青铜作为开口圆柱薄壳的材料.铍青铜经过热处理工艺后具有良好的弹性、强度和硬度，而且耐疲劳、耐腐蚀、耐低温、无磁性.铍青铜的主要材料参数值如表1所示.

表1 铍青铜的材料参数

2 特征值屈曲分析

2.1 基础理论

设薄壳结构在载荷状态P0下满足:

式中，Ke为结构的弹性刚度矩阵;u0为结构在P0作用下产生的位移.

假设位移足够小，则在任意状态下的增量平衡方程为

式中，Kσ(σ)是应力状态σ下的应力刚度矩阵.式(2)表达了结构内的应力状态对结构净刚度的增强或削弱效应.

设加载行为是载荷P0的线性函数，即

不考虑任何非线性情况，则有

式中σ0为载荷P0状态下结构内部的应力.于是，增量平衡方程变为

当结构发生屈曲时，在ΔP=0的情况下仍然会产生位移增量Δu≠0，即

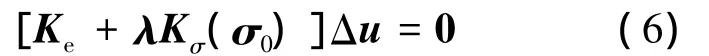
方程(6)代表了线性屈曲的特征值问题，λ被称为特征值或载荷因子，它的最小值与初始载荷P0的乘积即为结构的屈曲载荷.

2.2 特征值屈曲载荷的有限元求解

应用有限元软件ANSYS建立开口圆柱薄壳的有限元模型，如图2所示.模型包括两部分:作为分析对象主体的薄壳和对薄壳进行固定的紧固圈.其中，薄壳部分使用弹性壳单元SHELL63，两端的紧固圈使用三维结构实体单元SOLID45.

由于结构的形状较为简单，因此在划分单元时采用正交型网格，即薄壳部分为四边形单元，紧固圈部分为六面体单元.由于单元在横截面上是以多边形来逼近圆周，因此周向上应划分足够多的单元，一般整个圆周上应不少于72个.另外，为了保证单元具有良好的形状，单元的长短边的长度之比应小于3∶1.

图2 薄壳有限元模型

在设置单元材料参数方面，薄壳部分采用表1中QBe2的材料参数值，紧固圈部分则采用钢材或铝材的材料参数均可.

对有限元模型的一端施加总和为1 N的均布载荷，且加载端节点只具有轴向平动自由度;而模型另一端节点的6个自由度则被完全约束.

在特征值屈曲分析过程中，首先要进行静力学求解来获得结构载荷与位移之间的线性关系，然后再进行特征值屈曲求解，提取特征值与屈曲模态.需要注意的是，在进行静力学求解时必须激活预应力效应.

3 屈曲载荷模型的推导

3.1 模型基本形式

根据文献［13］的结论，可以得到轴压开口圆柱薄壳在两端简支情况下的屈曲载荷模型为

式中，屈曲载荷PCR，弹性模量E，厚度t，扇角θ的单位分别为 N，Pa，mm，(°).从式(7)可以看出，该模型中不包含薄壳长度L和曲率半径R两项，即认为轴压开口圆柱薄壳的屈曲载荷与薄壳长度和曲率半径无关，而这与实际情况是不相符的.

本文的研究中采用单变量拟合的方法，设置几何参数单独变化的序列，并逐一进行特征值屈曲分析，用幂函数对每个序列的分析值进行拟合，以此来推导轴压开口圆柱薄壳在两端固支条件下的屈曲载荷模型.

首先，参考文献［13］的模型，设各向同性材料的开口圆柱薄壳在两端固支条件下受轴压作用时的特征值屈曲载荷分析值PEV与薄壳几何参数之间的关系满足:

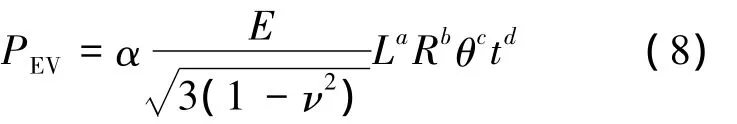
式中，α 为待定系数;a，b，c，d 分别为薄壳长度、曲率半径、厚度和扇角项对应的指数.即式(8)中共包含5个需要确定的参数.

3.2 模型推导过程

模型推导的过程即是确定式(8)中5个未知参数的过程.首先通过单变量拟合的方法分别研究PEV随开口圆柱薄壳各几何参数的变化趋势，即确定a，b，c，d的值;再通过求解平均值的方法确定系数α的值.

为了研究PEV与薄壳长度L的关系，设定薄壳的曲率半径和厚度为R=15 mm，t=0.2 mm，设置薄壳扇角分别为 θ=120°，θ=180°和 θ=240°的3个长度序列，对长度L在60～360 mm之间的开口圆柱薄壳进行特征值屈曲分析，并使用幂函数对分析值进行拟合，如图3所示.从图3中可以看出，当 θ=240°时，屈曲载荷 PEV与 L－0.2成正比;当 θ=180°时，大多数分析值满足 PEV与 L－0.2成正比，但在L=300～330 mm之间曲线出现了转折点;当θ=120°时，在L=120 mm附近即出现转折点，此后屈曲载荷PEV与L－1.5成正比.由此可知，转折点的位置不仅仅与薄壳长度L有关，还需考虑其他几何参数.在转折点之前，式(8)中长度项L 的指数 a=－0.2，转折点之后 a=－1.5.

图3 PEV-L曲线(R=15 mm，t=0.2 mm)

设定薄壳厚度为t=0.2 mm、扇角为θ=240°，设置L=60mm，L=180mm和L=300mm 3个曲率半径序列来分别进行特征值屈曲分析，并对分析值进行拟合，如图4所示.由图4可见，薄壳长度越大，转折点对应的曲率半径越大.在转折点之前，PEV与R2.4成正比，即式(8)中曲率半径项R的指数 b=2.4;在转折点之后，PEV与 R0.1成正比，即 b=0.1.

设定薄壳的曲率半径 R=15 mm、厚度 t=0.2 mm，设置 L=60 mm，L=180 mm 和 L=300 mm 3个扇角序列来研究特征值屈曲载荷PEV与薄壳扇角θ的关系，如图5所示.从图5中可以看出，薄壳的长度越大，转折点对应的扇角也越大.在转折点之前，屈曲载荷PEV与θ3.5成正比，即式(8)中扇角项θ的指数c=3.5，在转折点之后，PEV与θ成正比，即c=1.

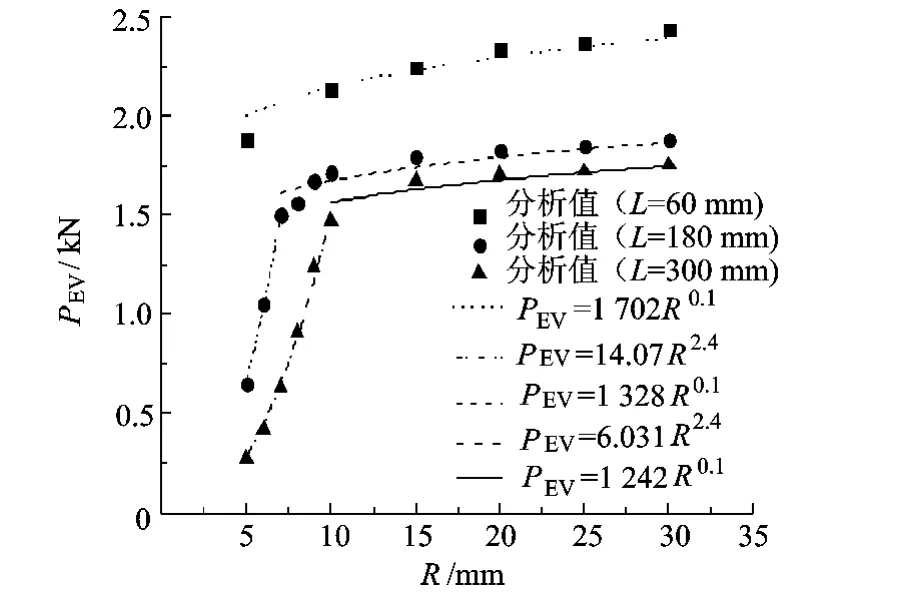
图4 PEV-R 曲线(t=0.2 mm，θ=240°)

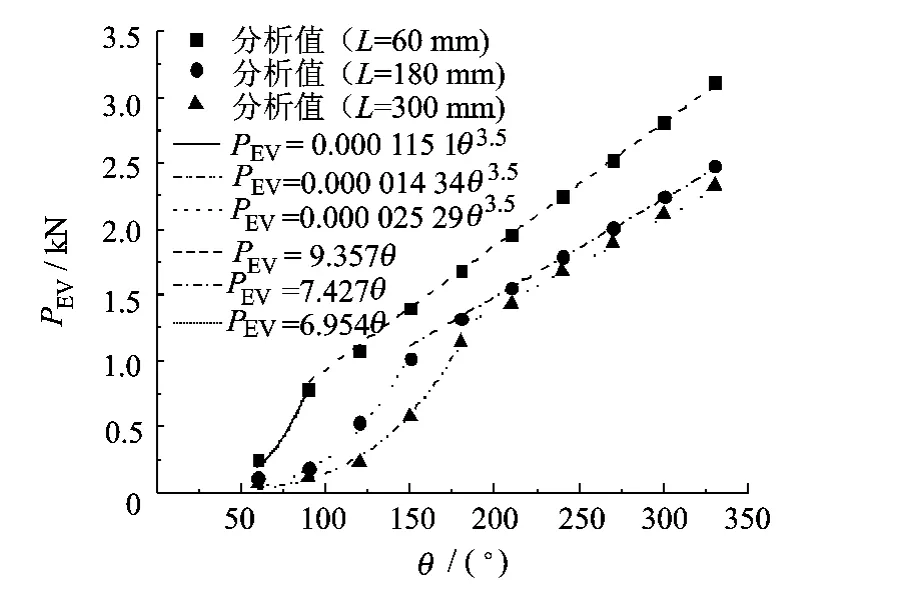
图5 PEV-θ曲线(R=15 mm，t=0.2 mm)

薄壳特征值屈曲载荷PEV与薄壳厚度之间的关系较为独立.设定 L=180 mm，R=15 mm，θ=240°，对不同厚度的壳体进行特征值屈曲分析，并对分析值进行拟合，如图6所示.由图6可见，特征值屈曲载荷PEV与t2成正比，即式(8)中厚度项t的指数d=2.

图6 PEV-t曲线(L=180 mm，R=15 mm，θ=240°)

根据转折点处薄壳长度L、曲率半径R和扇角θ之间的关系，定义转折点判定参量为

式中，x，y分别为曲率半径R和扇角θ的指数，其值待定.在转折点处，Z=Z0，Z0即为转折点的判定阈值.

于是，式(8)可以按照判定参量Z与阈值Z0的关系表达成一个分段函数:

式中，α1，α2为对应两种情况下的待定系数，从已有的数据来看，α1与α2在各自情况下都是基本保持一致的.因此，根据已有的薄壳几何参数值与屈曲载荷分析值，便可求出α1和α2的平均值为:α1=5.0×10－9，α2=3.2×10－14.再根据函数的连续性，可以求得 x=1.8，y=1.9，Z0=1.0×10－4.

于是，建立各向同性材料的开口圆柱薄壳在两端固支条件下受轴压作用时的屈曲载荷模型(BLOOM，Buckling Load of Open cylindrical thin shells Model)为

式中，Z=L/(R1.8θ1.9)，为判定参量;其中长度 L，曲率半径R的单位为mm.

4 轴向压缩试验

4.1 试件与试验设备

为了验证特征值屈曲分析以及屈曲载荷模型的准确性，对9组不同几何参数的开口圆柱薄壳按每组5个试件的规模进行了轴向压缩试验.

45个铍青铜开口圆柱薄壳试件均采用手工制作.首先对铍青铜带材进行790℃下保温8 min的固溶处理，淬火后对其进行剪裁与成型工艺，之后再进行320℃下保温2 h的时效处理.经过上述工艺后，所获得试件的圆柱度公差在毫米量级，弹性模量略低于表1中所列的数值.加工完成的9组试件如图7所示，其几何参数如表2所示.

图7 压缩试验试件

表2 试件几何参数

压缩试验使用REGER RGM-3100型电子万能试验机，其静态载荷测量精度为示值的±1%.首先将试件的两端用喉箍和垫片箍紧，再通过特制的夹具将其安装于试验机的压头与平台之间，如图8所示.

图8 试件安装示意图

试验机与一台计算机相连接，由计算机控制试验过程以及采集处理试验数据.进行压缩试验时，以20mm/min的加载速度对试件缓慢加载，由于屈曲是在瞬间发生的，而计算机采样频率的限制使其很难采集到屈曲载荷的峰值，因此也会使试验结果产生一定的误差.

4.2 试验结果及讨论

以 L=180 mm，R=15 mm，t=0.2 mm，θ=120°的第6组第3号铍青铜开口圆柱薄壳试件为例，试验获得的载荷-位移曲线如图9所示，临近屈曲时的试件形状如图10所示.图11是使用有限元法进行特征值屈曲分析时所得到的屈曲模态图.将图10与图11进行比较可以发现，试件临近屈曲时的形状与分析得到的屈曲模态较为相似，但屈曲模态中的挠度更为显著.

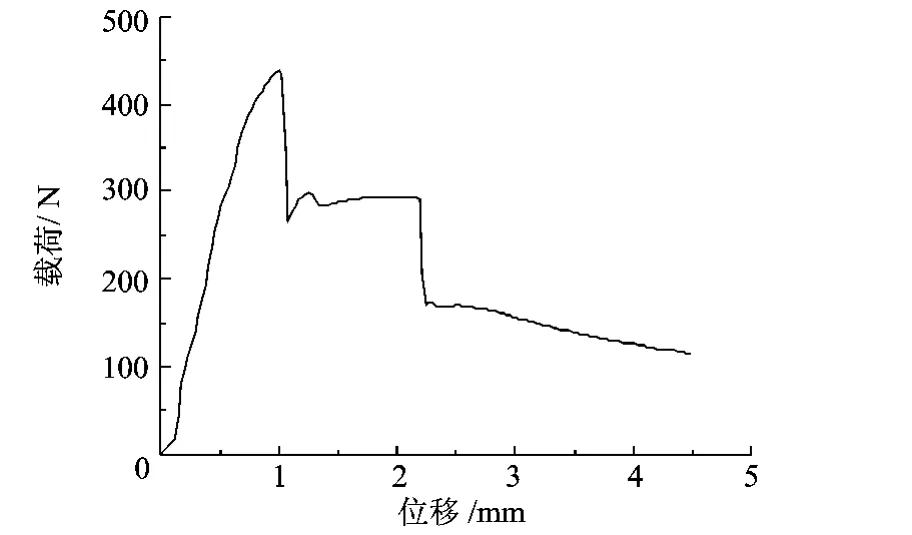
图9 试验载荷-位移曲线

图10 临近屈曲时的试件形状

图11 屈曲模态示意图

将轴向压缩试验得到的开口圆柱薄壳屈曲载荷试验结果与特征值屈曲分析结果和屈曲载荷模型计算结果进行比较，如表3所示.其中，相对误差的计算均以各组试验的平均值作为真值.

表3 试验结果与分析结果、计算结果的比较

由表3中试验结果可见，试验值的分布往往较为离散，标准差较大.其主要原因在于，试件在加工和安装阶段所产生的形位公差，以及淬火时冷却不均产生的材料缺陷，都会导致同组试件的屈曲载荷有所不同.

由表3中特征值屈曲分析结果可见，除第2组和第6组外，轴压开口圆柱薄壳在两端固支条件下的特征值屈曲分析值与试验平均值较为接近，所有分析值均在(±3σ)范围内.

由表3中BLOOM计算结果可见，计算值与特征值屈曲分析值较为接近，拟合情况较好.与试验均值相比，Z≤1.0×10－4时 BLOOM 的计算误差在±10%以内，Z＞1.0×10－4时的计算误差较大，最大为21%.

5 结论

本文通过对各向同性材料的开口圆柱薄壳在两端固支条件下受轴压作用时的一系列分析与试验研究，可以得到以下结论:

1)特征值屈曲分析结果与试验均值基本一致，因此可以采用特征值屈曲分析方法来求解各向同性材料的开口圆柱薄壳在两端固支条件下受轴压作用时的屈曲载荷.

2)经过试验验证，使用单变量拟合方法所推导的屈曲载荷模型BLOOM适用于估算各向同性材料的开口圆柱薄壳在两端固支条件下受轴压作用时的屈曲载荷，计算值与试验均值相比，最大误差为21%.

References)

［1］Pellegrino S.Large retractable appendages in spacecraft［J］.Journal of Spacecraft and Rockets，1995，32(6):1006－1014

［2］陈烈民.航天器结构与机构［M］.北京:中国科学技术出版社，2005:312－321

Chen Liemin.Spacecraft structures and mechanisms［M］.Beijing:China Science and Technology Press，2005:312－321(in Chinese)

［3］Higuchi K，Ishimura K.A survey of space structures research in Japan［R］.AIAA-2009-2387，2009

［4］杜启端.现代薄壳非线性稳定性理论的发展和应用［J］.强度与环境，2002，29(1):41－51

Du Qiduan.Advance and application for the modern nonlinear stability theory of the thin shell［J］.Structure ＆ Environment Engineering，2002，29(1):41－51(in Chinese)

［5］Karman T V，Tsien H.The buckling of thin cylindrical shells under axial compression［J］.Journal of the Aeronautical Sciences，1941，8(8):303－312

［6］Donnell L H，Wan C C.Effect of imperfections on buckling of thin cylinders and columns under axial compression［J］.Journal of Applied Mechanics，1950，17(1):73－83

［7］Koiter W T.On the stability of elastic equilibrium［D］.Delft:Department of Mechanics，Shipbuilding，and Airplane Building，Delft University of Technology，1945(in Dutch with English summary)

［8］沈惠申，陈铁云.圆柱薄壳在外压作用下屈曲的边界层理论［J］.应用数学和力学，1988，9(6):515－528

Shen Huishen，Chen Tieyun.A boundary layer theory for the buckling of thin cylindrical shells under external pressure［J］.Applied Mathematics and Mechanics，1988，9(6):515－528(in Chinese)

［9］Chu K H，Krishnamoorthy G.Buckling of open cylindrical shells［J］.Journal of the Engineering Mechanics Division，1967，93(2):177－205

［10］Chu K H，Turula P.Buckling of open cylindrical shells under axial load［J］.Journal of the Engineering Mechanics Division，1970，96(6):1143－1156

［11］Yang T H，Guralnick S A.Buckling of axially loaded open shells［J］.Journal of the Engineering Mechanics Division，1976，102(2):199－211

［12］Silver M J，Warren P，Hinkle J D，et al.Buckling of curved shells with free edges under multi-axis loading［R］.AIAA-2006-2100，2006

［13］Magnucka-Blandzi E，Magnucki K.Elastic buckling of an axially compressed open circular cylindrical shell［J］.Proc Appl Math Mech，2004，4(1):546－547

［14］Magnucki K，Makiewicz M.Elastic buckling of an axially compressed cylindrical panel with three edges simply supported and one edge free［J］.Thin-Walled Structures，2006，44(4):387－392

［15］Wilde R，Zawodny P，Magnucki K.Critical state of an axially compressed cylindrical panel with three edges simply supported and one edge free［J］.Thin-Walled Structures，2007，45(10 －11):955－959