常值径向推力下的飞行器运动轨迹

张 皓 师 鹏 赵育善 李保军

(北京航空航天大学 宇航学院，北京100191)

常值径向连续推力机动是常用的轨道机动方式，文献［1－7］对这类问题进行了研究.早在1953年，文献［1］就研究了二体模型下使用常值径向推力逃离中心引力场的问题.后来文献［2］用椭圆积分求解了初始轨道为圆轨道的情形.1998年，文献［3］引入势能阱的概念，研究了从圆轨道逃逸的条件和不发生逃逸时飞行器所能达到的最大半径.文献［4］研究了利用常值径向推力轨道来构建非开普勒［8］意义下的圆轨道的方法，并与开普勒圆轨道进行了对比.然而对初始轨道为椭圆的研究文献还很少.文献［5］利用动力系统理论，通过数值积分得到了一些特殊的周期轨道，并分析了其稳定性.文献［6］通过几何作图法，得到了椭圆轨道下逃离中心引力场时所需的最小推力.针对椭圆初始轨道情况的解析性质研究，目前还很少有文献提及，此类研究对将来的空间应用具有重要的意义，例如运动可达区［9］的分析和深空轨道的设计等.

本文考虑初始轨道为椭圆，施加常值径向连续推力后飞行器的运动轨迹，并从解析角度对这一特殊轨迹的有界性和周期性进行研究.首先建立了运动微分方程，并通过首次积分，将运动写成求积的形式;然后通过研究一个三次多项式的根，分析了运动的有界性;最后用椭圆积分研究了运动的周期性并给出了周期轨道的求法.

1 基本方程

定义航天器施加推力前所处的开普勒轨道为停泊轨道，设该停泊轨道半长轴为a，偏心率为e.初始时刻t0航天器的真近点角为f，从此刻开始施加常值径向推力.不考虑航天器质量变化，设推力加速度为ar.由于仅受径向力的作用，航天器的轨道角动量守恒，运动将局限在停泊轨道所在平面内［3］.为方便研究，在此停泊轨道平面内建立极坐标系，以引力中心为坐标原点，以停泊轨道近地点方向为极轴方向，航天器运动方向为极角增加的方向，如图1所示.

图1 坐标系定义

选取极角θ和地心距(极距)r为运动的广义坐标，建立运动的极坐标方程为

式中，μ为中心体的引力常数;ar沿径向向外为正.

由于常值径向推力可以看作引力势的一部分，即

故该系统为保守系统，存在能量积分E.另一方面，由于原点在推力方向上，不改变系统的角动量，因此存在角动量积分H.

上述的两个积分可以表示为

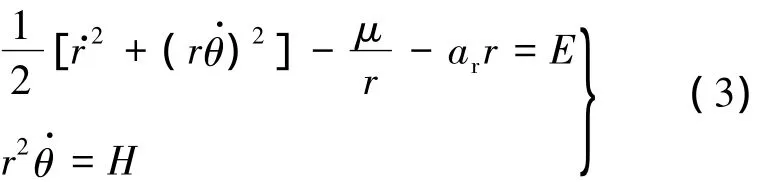
由于该积分为常值，可以用初始条件表示:

式中，E0=－μ/2a和H0=［μa(1－e2)］1/2分别为原停泊轨道的能量和角动量;r0=a(1－e2)/(1+ecosf)为初始时刻的地心距.利用积分可将运动方程(1)化成一阶微分的形式:

对式(5)分离变量后直接积分可以得到r关于t的表达式，然而在积分过程中需要用椭圆函数［10］，且涉及变量代换，形式比较复杂，为更好地得到常值径向推力下的轨迹特性，本文避免冗长的解析表达，而对其进行定性研究.

2 运动有界性分析

如果要利用径向推力逃逸中心体的中心引力场，需对运动的有界性进行研究.

2.1 运动的边界以及临界条件

在式(5)的第1式中存在根式，因而要使其有意义，需满足如下关系［11］:

式(6)为一元三次不等式，通过对该式的分析，可以得到运动的范围.令不等式(6)对应的一元三次多项式为F(r)，称之为基本多项式［7］:

如果F(r)=0仅有一个实根r1，那么不等式(6)的解为r＞r1，从而易知其运动是无界的.对于有界运动，F(r)=0必然有多于一个实根.不失一般性，假设方程F(r)=0有3个不等实根，从小到大依次为r1，r2和r3，那么不等式(6)的解可写成:

若r0∈［r1，r2］，则其运动有界，且运动边界分别为r1和r2，运动轨迹限制在半径分别为r1和r2的同心圆环内;否则其运动无界.从式(4)可以看到，当初始a，e和f确定后，方程F(r)=0的根只取决于ar，它决定了方程实根的个数以及在数轴上的分布，从而影响运动的有界性.本文将有界运动和无界运动的分界推力称为临界推力，用arc表示.

虽然式(6)的根可以利用求根公式［10］求解，但求根公式太过复杂，不易看出规律.当初始位置比较特殊时，式(6)可以分解因式，从而可以得到运动边界以及临界推力的简单表达式［7］.例如，当初始位置位于停泊轨道的近地点时，运动的临界推力为

当ar＞arc时运动无界，否则运动有界，且其边界由下式确定:

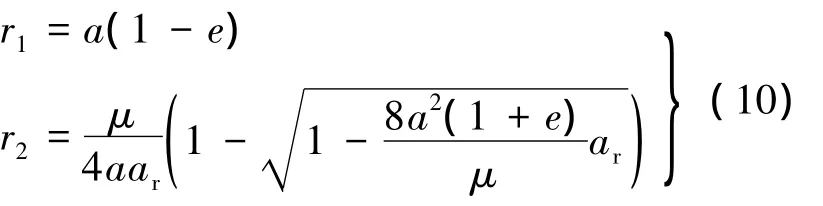
当初始的位置位于停泊轨道的远地点，也存在类似的结论，此时arc的表达式还和e有关:

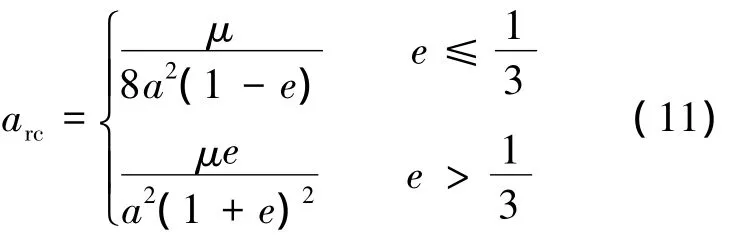
同样，当ar＞arc时运动无界，否则运动有界，且其边界由下式确定:

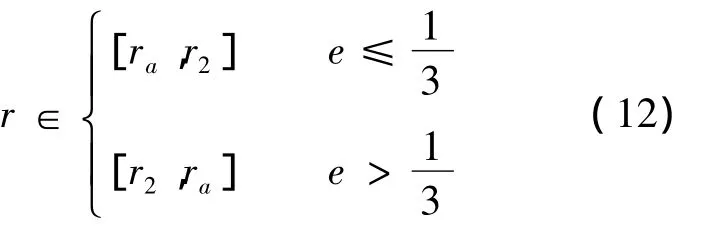
对于一般的初始位置 0＜f＜π 或 π＜f＜2π，不能得到类似的简单表达式，但仍然可以用类似的方法进行分析.通过研究式(6)的根的情况，可以得到一般情况下arc的表达式［7］:

式中，ε是方程(14)的最小实根.

有界运动的运动边界需求解F(r)=0，此时方程有3个实根，边界由其最小的两个实根决定，即运动范围r∈［r1，r2］.

另外，随着推力ar的变化，方程F(r)=0的根也会发生变化.可以证明［7］，随着ar的增大，r1和r2增大而r3减小，且当ar=arc时，方程的根r2和r3重合，但都大于r1，如图2所示.本文算例都使用无量纲的引力常数μ=1，后面不再说明.图2取a=1，e=0.8，f=170°.

图2 方程F(r)=0的根随ar的变化趋势

2.2 边界上的运动分析

由前面的分析可知，运动的有界性主要由r的可行范围决定，下面分析r达到边界之后的运动趋势.将式(5)的第1式对时间求导并利用F(r)=0的实根，得到r相对于时间的二阶导数:

在内边界处，有r=r1，代入式(15)和式(5)的第1式，得到

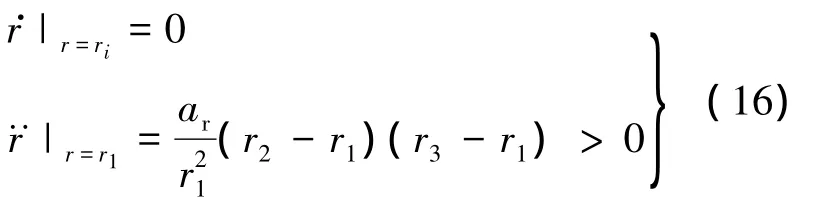
在外边界处，有r=r2，代入式(15)和式(5)的第1式，得到

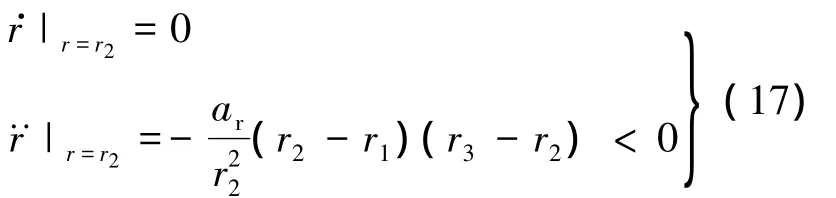
从式(16)和式(17)可以看出:当运动到达内边界时，r相对于时间的一阶导数为0，二阶导数为正，因此其向着r增大的趋势运动.当运动到达外边界时，r相对于时间的一阶导数为0，二阶导数为负，因此向着r减小的趋势运动.

特殊情况，当ar=arc时，r1＜r2=r3.由式(17)可知，当航天器运动到外边界r2时，和都为0，r不再增大或者减小，运动的轨迹形成一个圆形.这一圆形是典型的非开普勒轨道［8］，文献［4］对停泊轨道为圆时的这类轨道进行了分析，并且和开普勒圆轨道进行了对比.

3 运动周期性分析

3.1 运动的拟周期性

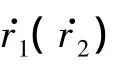
其中，dr＞0时取正号，dr＜0时取负号.从式(18)容易分析运动时间和极角的变化情况.

定义径向从某次内边界运动到下一次内边界的运动时间为径向周期，以Tr表示.这一概念类似于椭圆开普勒轨道的轨道周期.Tr可以表示为

式(19)可以用椭圆积分［10］表示:

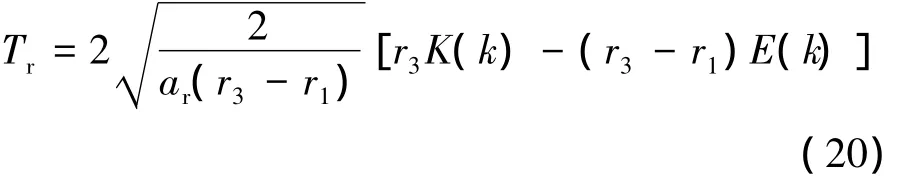
注意，当初始位置固定时，Tr仅决定于ar，因此可以看成ar的单变量函数，即Tr(ar).

描述轨道运动的另外一个重要参数是θ.由前可知，运动在内外边界循环一次，其时间为一个径向周期，由式(18)的第2式可知这一过程中极角的变化Δθr(称为极角转动)为

式(21)同样可以用椭圆积分表示:

这里的特征数n＜0，为利用文献［10］给出的计算方法，需要将式(22)的椭圆积分转化为标准形式［10］(n位于0和1 之间)，即

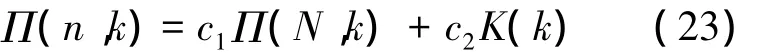
式中，系数c1，c2和新特征数N分别为

此时有k2＜N＜1，满足第3类完全椭圆积分标准形的要求.

由式(22)可以看到，每完成一次径向循环航天器转过的极角Δθr也是相同的.当初始位置确定，Δθr仅决定于ar，因此可以看成ar的单变量函数，即 Δθr(ar).

考虑某次内边界r1前后到任意极距r的极角变化，分别用Δθf和Δθb表示:

容易看到

因此轨迹具有径向对称性，即运动轨迹关于近地点方向是对称的，同样可知其关于远地点方向也是对称的.

航天器的整体运动可以看成径向运动和极角转动的合成，表现为一个进动的椭圆.椭圆的近地点和远地点各自在半径为r1和r2的圆上漂移.如果一个径向周期内，航天器的极角转动满足:

式中，p，q分别是互质的整数，那么其运动是周期性的，否则其运动为拟周期的，其轨迹将会布满整个运动可行区域.这类似于平面上的振子，当各个方向振动频率不同时，其运动的轨道会布满整个相平面［12］.图3给出了一个运动的实例，参数分别为 a=1，e=0.5，f=120°，ar=0.08，从中可以看出运动的径向对称性和拟周期性.

图3 运动轨迹

另一方面，Tr和Δθr都可以看成ar为自变量的单变量函数.计算可知，随着ar的增加，Tr和Δθr都增大.当ar=0时，运动轨迹就是停泊轨道，此时Tr为停泊轨道周期T0，Δθr=0;当ar=arc时，航天器一旦到达外边界，之后一直沿着该边界运动，因此可看作Tr和Δθr为无穷大.因此对于有界运动，Tr和Δθr的取值范围是

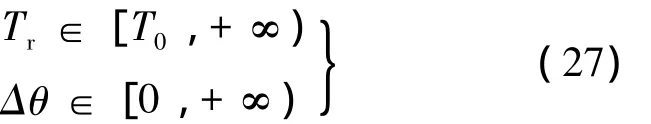
取 a=1，e=0.5，f=120°，Tr和 Δθr随着 ar的变化如图4所示.

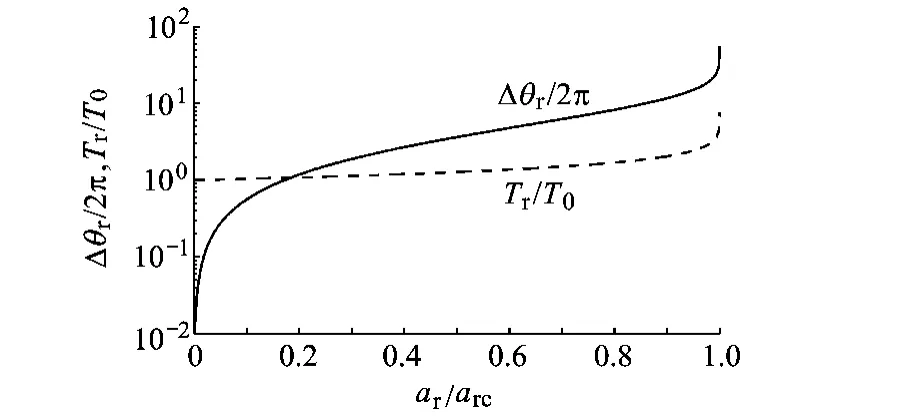
图4 Tr和Δθr随推力大小的变化

3.2 周期轨道

从3.1节的分析可知，当Δθr满足:

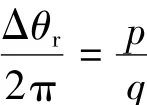
运动具有周期性，且运动的周期为qTr.由于整体运动的周期仅与q有关，称q为周期特征数.通过上式求反函数，可得所需的推力ar，即

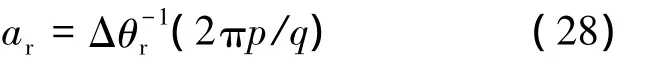
求解式(28)会遇到以下的问题，下面逐一说明.

1)虽然利用式(28)解析求解ar是可行的，然而Δθr的表达式(22)用到了椭圆积分，使得ar具体的形式过于复杂，因此本文将用迭代方法求解.

2)迭代时需知道Δθr对ar的导数，而ar对Δθr的部分影响是通过方程F(r)=0的根 r1，r2和r3实现的，因此求导时不可避免要应用链式法则.文中r1，r2和r3和椭圆积分的参数有关.椭圆积分本质是一个无穷限的广义积分，对其求导会出现无界函数，在数值计算中会出现困难，因此本文采用差分导数.

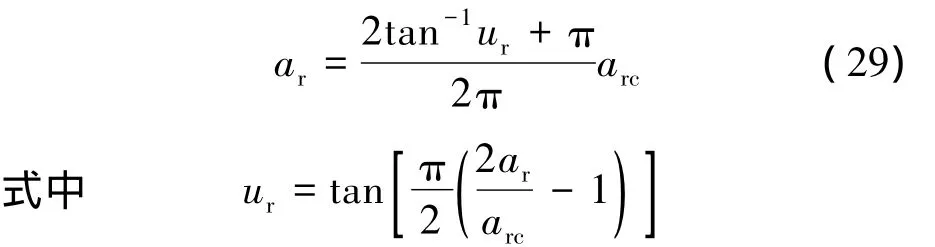
3)由于周期轨道是有界运动的特例，因此ar的求解范围应限制在区间［0，arc］上.迭代过程中可能会有某次迭代值超出区间［0，arc］，如图5所示.为避免这一现象对于求解的不利影响，考虑使用如下的单调映射:

将求解范围从［0，arc］变换到(－∞，+∞)，将求解变量从ar转化为ur.通过数值验证发现，采用这样的代换还可以加快收敛速度.

图5 迭代出界示意图

4)迭代初值对于算法的收敛性影响很大.经过式(29)变换后，收敛性可以得到较好的保证.为简单起见，文中选择ar0=arc/2，对应于变换后的变量ur0=0.

算例:为使仿真图形简单，本文只考虑简单分数的情形，即p和q至少有一个为1.

1)多周期轨道.指 p=1，q＞1的情况，即 Δθr完成一次循环的同时径向运动要完成q次循环.这里的多周期是相对于径向运动的周期而言的.

给定如下仿真参数:设 a=1.41，e=0.418，f=60°.当 p=1，q=3 时，ar=0.045579211004;当 p=1，q=2 时，ar=0.046 327 987 567.迭代精度取10－12，仿真中积分器选用 MATLAB®ODE45，仿真精度为 10－12.

仿真结果如图6，每个图都含有4种曲线，即停泊轨道、运动轨迹、内边界和外边界.图6a对应p=1，q=3的情况，可以看到径向运动经过3个周期，极角转动完成一次循环;图6b对应p=1，q=2的情况，即径向运动经过两个周期，极角转动完成一次循环.

2)单周期轨道.指p≥1，q=1的情况，即径向完成一次循环，极角已完成了多个循环.

取a=1.41，e=0.418，f=180°.当p=1，q=1 时，ar=0.100000000057;当 p=2，q=1 时，ar=0.103953507 988.迭代精度取10－12，仿真精度为10－12.

仿真结果如图7，图7a对应p=1，q=1的情况，可以看到径向运动经过一个周期，极角转动也刚好完成一次循环;图7b对应p=2，q=1的情况，径向运动经过一个周期，极角完成两次循环.

图6 多周期轨道仿真算例

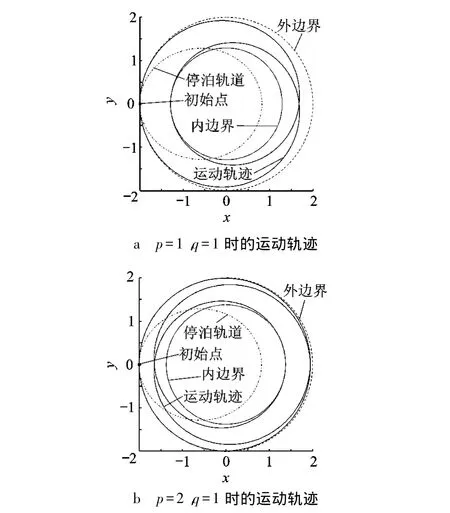
图7 单周期轨道仿真算例

可以用类似的方法构建不同周期的轨道，这里不再赘述.

4 结束语

本文分别从有界性和周期性研究了椭圆停泊轨道上常值径向推力下飞行器的运动轨迹.研究表明运动存在有界和无界两种情况，其分界由临界推力确定.对某些特殊的情况，可以写出运动边界和临界推力的简单表达式.应用椭圆积分研究了有界运动的周期性，结果表明运动具有拟周期性，即径向运动和极角的变化都有周期性，当这两个周期通约时，可以得到周期轨道.文中最后给出了一种获取周期轨道的数值算法.本文的结果可以用来进行深空小推力轨道的初步设计等.

References)

［1］Tsien H S.Take-off from satellite orbit［J］.Journal of the American Rocket Society，1953，24(4):233－236

［2］Battin R H.An introduction to the mathematics and methods of astrodynamics［M］.Revised Edition.Reston，VA:AIAA，1999:408－415

［3］Prussing J E，Coverstone-Carroll V.Constant radial thrust acceleration redux［J］.Journal of Guidance Control and Dynamics，1998，21(3):516－518

［4］周姜滨，袁建平，罗建军.空间飞行器连续径向推力机动轨道研究［J］.宇航学报，2009，30(1):67－71

Zhou Jiangbin，Yuan Jianping，Luo Jianjun.Spacecraft orbits under continuous radial thrust［J］.Journal of Astronautics，2009，30(1):67－71(in Chinese)

［5］Akella M R，Broucke R A.Anatomy of the constant radial thrust problem［J］.Journal of Guidance Control and Dynamics，2002，26(3):563－570

［6］Mengali G，Quarta A.Escape from elliptic orbit using constant radial thrust［J］.Journal of Guidance Control and Dynamics，2009，32(3):1018－1022

［7］张皓，李保军，赵育善.常值径向推力下飞行器运动的可行域研究［C］//袁建平.空间操作自主控制专题研讨会论文集.长沙:国防科技大学，2009:509－516

Zhang Hao，Li Baojun，Zhao Yushan.Feasible region of spacecraft with a constant radial thrust［C］//Yuan Jianping.Seminar on Space Operation and Autonomous Control.Changsha:National University of Defense Technology，2009:509－516(in Chinese)

［8］袁建平，朱战霞.空间操作与非开普勒运动［J］.宇航学报，2009，30(1):42－46

Yuan Jianping，Zhu Zhanxia.Space operations and non-keplerian orbit motion［J］.Journal of Astronautics，2009，30(1):42－46(in Chinese)

［9］Xue Dan，Li Junfeng，Baoyin Hexi，et al.Reachable domain for spacecraft with a single impulse［J］.Journal of Guidance Control and Dynamics，2010，33(3):934－942

［10］Abramowits M，Stegun I A.Handbook of mathematical functions with formulas，graphs，and mathematical tables［M］.Ninth Printing.New York:Dover，1972:17，567－684

［11］Vinti J P.Orbital and celestial mechanics［M］.Reston，VA:AIAA，1998:58

［12］Hirsch M W，Smale S，Devaney R L.Differential equations，dynamical systems，and an introduction to chaos［M］.Second Edition.San Diego，CA:Academic Press，2004:114－119