基于网络流仿真的潜通路分析方法
2012-06-22马齐爽
邹 涛 马齐爽
(北京航空航天大学自动化科学与电气工程学院,北京 100191)
潜通路分析是一种非常有效的可靠性分析方法,揭示了电路中非器件失效而由于潜通路的存在所引起的系统功能异常[1-2].潜通路的分析目的就是找到电路中各个功能是否被正确的激活,不存在期望功能被抑制或者激活非期望功能的情况.目前主要有3类潜通路分析方法:人工的潜通路分析方法,半自动或者计算机辅助的潜通路分析方法以及智能化、自动化的潜通路问题分析方法[3].
线索表潜通路分析法是一种计算机辅助方法,主要工作过程是通过人工分析化简,得到电路的线索表,设置需要分析的电路状态以后,通过计算机对线索表进行遍历,得到电路在所有状态下的通路,分析这些通路,最后确定电路是否存在潜通路问题.随着电路拓扑的扩大与复杂程度增高,电路的线索表变得更加难以获取.在分析过程中,人为参与较多,化简电路存在着越来越大的不可靠因素,可能会丢失一些重要的分析信息,而且处理时间会随着电路拓扑的扩大而增加;同时,通过线索表法得到电路对应状态下的所有路径,这些路径包含了正常路径以及存在潜通路问题的路径,需要进行人工判断来分辨这些路径.因此,线索表法在潜通路分析中具有一定的局限性[4].为了克服线索表法的局限性,提出了许多智能潜通路分析方法,其中人工神经网络分析法是其中一种.人工神经网络分析法利用训练过的神经网络预测所有开关组合下系统实现的功能,通过与设计响应比较判断是否存在潜通路问题.这种潜通路分析方法克服了线索表法的一些缺陷,避免了线索表难以获取的问题以及减少了人工分析时间[5].但是在分析过程中,有可能难以获得全部开关组合的负载响应.由于电路负载的设计响应不完全,缺少足够的训练样本,难以保证得到正确的预测结果.
本文在人工神经网络潜通路分析方法的基础上,对其进行改进,得到了一种基于网络流仿真的潜通路自动分析方法.
1 建立电气元件与电路网络模型
神经网络模型是一种运算模型,由结点和结点之间的相互联接构成.每个结点代表一种特定的输出函数,每两个结点间的连接称为边.网络的输出则依据网络的连接方式和输出函数的不同而不同[6].在本文建立的人工神经网络模型中,电路中的元件将作为网络模型中的点,元件之间相互连接的导线作为网络模型中的边.对于网络模型中的边,由于构成电路的元件属性不同,将分为单向与双向两种,一般元件的默认连接都为双向边.对于网络模型中的点,需要对构成电路的元件进行分类,共有电源、地、控制类元件、受控类和中间元件等4类.
电源作为网络模型中的起点,与它相连的边全部为单向输出边,作为电流的输出;地作为网络模型中的终点,与它相连的边为单向输入边,作为电流的输入;控制类元件主要包括电路中的开关、继电器等控制类元件,这类元件的状态变化会引起网络模型拓扑的变化,与控制类元件相连的边的状态根据电路输入的不同表现为不同的状态;受控类元件为根据元件属性的不同,元件的输出函数不同,表现为与元件相连的边有可能为单向或者双向等,其余的元件为中间元件,这类元件的状态不随着控制类元件的变化而变化,始终保持状态不变.
半导体类元件也是一类重要的元件,这类元件可以起到控制作用或者对电流的流向做出的限制,所以这类元件的神经网络模型和控制类元件以及受控类元件不同,以二极管为例,二极管的神经网络模型如图1所示.

图1 二极管神经网络模型
在建立元件神经网络模型以后,根据元件的输出函数限制以及电路的拓扑结构建立电路的网络模型.电路的网络模型为矩阵形式,称为电路的基础矩阵.基础矩阵描述了电路的组成结构,并且是在所有开关全部为连通情况下的电路拓扑,这样描述了电路的所有连接,只需要调整开关状态就可以描述开关的不同状态组合.另外,还需要对电路网络的连接进行定义:一般元件之间由导线模型,也就是边相互连接;由于电源与地在网络流仿真过程中的特殊性,与它们相连的元件与电源和地等电位的点之间互不相连,这类电路的网络模型示意图如图2所示.
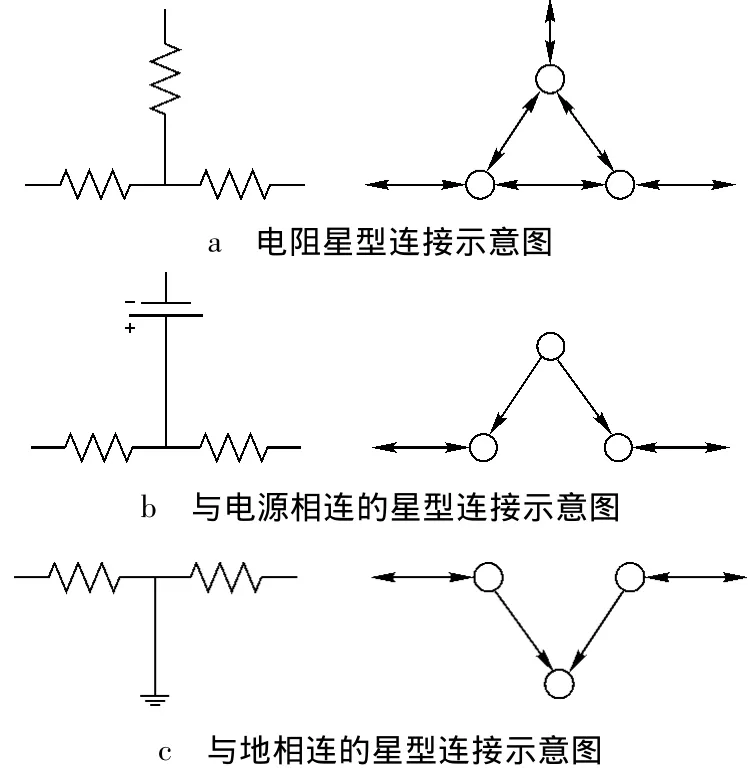
图2 星型连接网络模型
2 网络流理论与仿真应用
网络流是图论中的一个概念,是指在一个每条边都有容量的有向图分配流,使一条边的流量不会超过它的容量.其中,边有附带容量的图称为网络.所谓网络是指一个连通的赋权有向图D=(V,E,C),其中V为顶点集,E为有向边集,C为弧上的容量.此外顶点集中包括起点和终点.网络上的流就是由起点流向终点的可行流.一个网络可以用来模拟道路系统的交通量、管中的液体、电路中的电流或类似一些东西在一个结点的网络中游动的任何事物[7-8].
针对潜通路问题分析,可以把网络流仿真作为一种分析电流在电路网络中的动态过程分析方法.利用网络流仿真法,可以模拟电流在电路中的流动过程,最终得到负载的响应状态来进行潜通路分析.采用网络流仿真进行潜通路问题分析是一种定性仿真方法,定性仿真是一种建立系统的定性仿真模型并对其进行定性推理,对系统的定性行为以及工作状态进行分析的方法.在潜通路问题分析中,分析人员只关心系统中是否存在导致某些功能元件非期望的被激发或者被抑制的条件和路径.因此,在网络流仿真中,只需要描述元件的工作状态为工作或者不工作,网络中的边是否有电流通过即可,而不关心系统中的点和边的具体工作细节.
现在对有向图D进行定义.V是该图的顶点集,包括起点、终点和中间点.起点的入度为零,也称为源点,此点为电路图中的电源,作为电流流动的起点.终点的出度为零,也称为汇点,此点为电路图中的地,作为电流流动的终点.其他点为电路图中的其他元件,根据神经网络模型建立方法得到.潜通路分析只关心这些点的工作状态,因此定义“1”表示元件工作,“0”表示元件不工作.E是有向边集,根据电路中各个元件的连接关系以及限制条件得到.V和E共同组成了电路的网络模型.C是弧上的容量,由于采用定性仿真,定义“1”表示边有电流通过,“0”表示无电流通过.
在网络流仿真中,定义Vn为电路系统的状态向量,维数根据电路系统中的元件数量决定,每一个元件的工作状态都在当前状态的Vn中唯一对应.定义V0为电路系统的初始状态向量,作为迭代仿真的初始量.由于电路图已知,元件数量确定,因此V0的维数确定且与Vn相同.同时,V0中的“1”的数量根据电路中的电源数量确定,并且“1”的位置对应每一个电源.V0中的其他元件状态全部为“0”.定义MT为电路在当前状态下的变换矩阵.MT描述了电路中所有元件的连接关系,即描述了电路网络模型中左右的边的位置.由于电路中存在可以改变状态的元件,例如开关、三极管等,所以在不同的状态下,MT会进行改变.
确定潜通路的分析状态即开关的断开闭合状态后,得到确定的MT和V0,可以进行网络流仿真对负载响应进行预测.网络流仿真模拟了电流的扩散过程,这个过程通过状态变化来完成,假设当前状态为Vn-1,下一个状态为Vn,可以通过公式:

来确定 Vn,n=1,2,….当 Vn=Vn-1时,说明结果收敛,状态仿真结束.此时的Vn为当前分析状态下的电路各个元件的最终工作状态.
3 潜通路分析方法
本文研究的潜通路分析方法减少了对分析已知条件的要求,只需要所分析的电路图以及电路的设计响应MD即可.本文开发了自动处理程序进行潜通路分析.该程序使用SPICE 3F5版本的标准网表文件作为电路模型的输入,通过程序处理得到电路的神经网络模型.
读入网表文件以后,程序可以自动识别电路中的电源、地、控制类元件以及受控类元件和中间元件.然后根据预设的元件模型以及连接关系生成电路系统的神经网络模型.其中,元件模型的输出函数为网络模型中的点,元件相互之间的连接关系体现为电路的基础矩阵MB.MB描述了电路在所有控制类元件均为导通的状态下电路的连接关系,这表明了电路所有的点和边都连接在一起,电路的拓扑最完整.MB中行元素的定义就是该元件为起始点,连接到其他元件的边,列元素的定义就是该元件为终止点,其他元件连接到该元件的边.如果把一个元件在MB中对应位置的行和列全部清零,表明该元件不与其他任何元件连接.
控制类元件的工作状态可以分为工作“1”和不工作“0”,根据元件分类得到的控制类元件的数量,进行组合就可以得到电路的开关状态矩阵S,S={S1,S2,…,Sk}T.假设电路中的控制类元件数目为n,那么S中的行向量个数k=2n.
根据电路中的电源的数量以及建立MB时电源在矩阵中的位置,就可以得到电路的初始状态向量 V0.
前文叙述不同的开关状态对应不同的变换矩阵,因此MT可根据MB及S得到.将每一个开关状态向量中处于断开状态的控制类元件在MB中对应位置的行和列清零,就得到了当前状态下的MT.
网络流仿真法的输入量为V0以及MT,输出量为Vn.不同的开关状态向量生成不同的MT,同时得到对应的Vn.对所有的开关状态向量进行预测以后,通过整理Vn,提取Vn中负载的相应状态就可以得到电路的预测响应MF.当MD≠MF时,就表明电路存在潜通路问题.
4 潜通路算例分析
现在通过算例分析对基于网络流仿真的潜通路分析方法进行说明.飞机的起落架电路的电路图如图3所示.

图3 飞机起落架电路图
在算例中的货舱门和起落架在分析时用电阻代替,这样的代替不会影响分析的正确性.在正常的操作状况下,根据起落架放下开关的位置,决定起落架被放下或收起.货舱门仅在起落架预先放下且正常舱门打开开关合上后方可正常打开.在紧急状态下,货舱门可通过合上应急舱门打开开关代为打开,而不管起落架和正常舱门打开开关的状态.此电路设计的响应如表1所示,表中,“1”表示开关处于闭合状态或负载工作,“0”表示开关处于断开状态负载不工作.

表1 飞机起落架电路设计响应
根据神经网络模型建立方法,得到的电路的基础矩阵为

神经网络模型连接示意图如图4所示.
在分析过程中,U1,U2,U3为控制类点,其状态将确定MT的结构;R1,R2为受控类点,其状态响应为最终提取的结果.电路初始状态向量V0={1,0,0,0,0,0,0},以开关状态向量 S4={1,0,1}为例,电路变换矩阵为

图4 飞机起落架电路网络模型示意图

MT示意图如图5所示.

图5 MT示意图
电路最终状态向量 Vn={1,1,0,1,1,1,1}.对所有状态逐一进行负载响应预测,处理分析结果得到了预测响应,如表2所示.
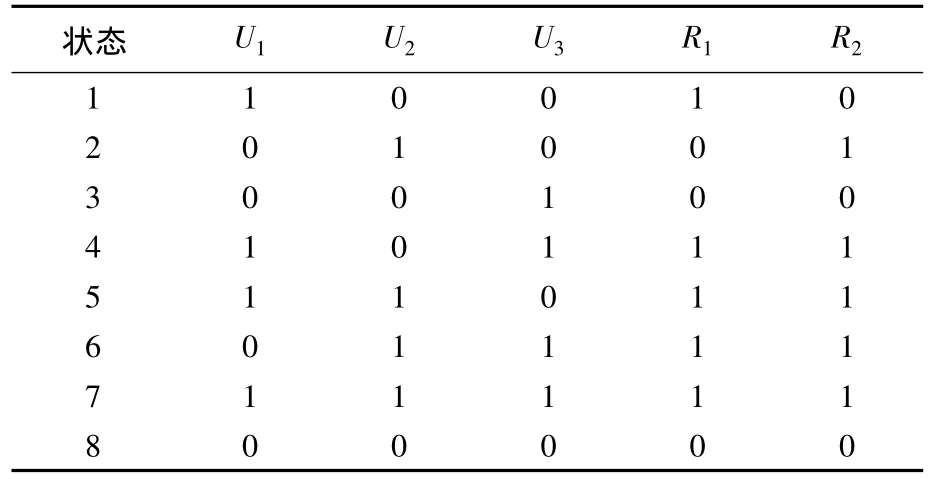
表2 网络流仿真预测响应
通过对比响应矩阵与设计响应,发现开关状态4对应的负载响应不正确,R2在此情况下被激活,与设计响应不符.由于程序可以自动保存网络流的扩散过程,因此调出该开关状态下的网络流扩散数据,即可发现存在
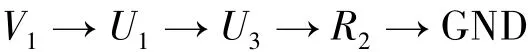
为非期望路径.
针对此电路问题,为了克服非期望功能的发生,对电路图进行改进,添加一个二极管来抑制非期望通路,则电路图变化如图6所示.
电路的设计响应不变,由于添加了一个二极管元件,则电路的神经网络模型发生变化,处理电路网表得到新的基础矩阵为


图6 更改后的飞机起落架电路
新的神经网络模型连接示意图如图7所示.

图7 新的神经网络模型示意图
同样以开关状态向量S4={1,0,1}为例,电路初始状态向量变为 V0={1,0,0,0,0,0,0,0},电路变换矩阵为

M'T示意图如图8所示.
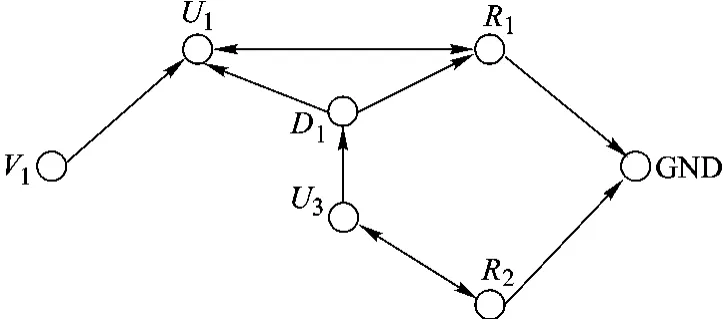
图8 M'T示意图
此时的电路最终状态向量为 V'n={1,1,0,0,1,0,0,1}.经过同样的分析过程,得到了该电路的网络流仿真预测响应,如表3所示.
预测响应与设计响应相同,说明发现的潜通路问题已经被解决且电路的解决方法有效.

表3 网络流仿真预测响应
5 结束语
本文针对线索表潜通路分析法的缺陷,在人工神经网络潜通路分析法的基础上,结合电路的神经网络模型以及网络流仿真法,分析电路中存在的潜通路问题.本方法可以定性地判断出电路中是否存在潜通路问题,在此基础上确认问题的具体位置.在分析初期,降低了分析所需的材料要求,并且在分析过程中减少了人工参与过程,避免了人为因素对最终分析结果的影响.本方法可以为潜通路问题判定提供参考依据,具有一定的应用价值.
References)
[1]Walker F E.Sneak circuit analysis automation[C]//Proceedings of theAnnualReliabilityand Maintainability Symposium.Atlanta:IEEE Computer Society,1989:502-506
[2]Rankin J P.Sneak circuit analysis[J].Nuclear Safety,1973,14(5):461-468
[3]胡昌华,陈斌文,刘丙杰.复杂系统潜在问题分析与应用[M].北京:科学出版社,2008:4-5
Hu Changhua,Chen Binwen,Liu Bingjie.Theory and application of sneak circuit analysis for complex system [M].Beijing:Science Press,2008:4-5(in Chinese)
[4]Zou Liping,Zou Tao.The application of neural network for sneak circuit analysis on the aircraft electrical system[C]//Prognostics and System Health Management Conference.Hongkong:City University of Hongkong Press,2011:1-5
[5]Zou T,Ma Q S.The research of sneak circuit analysis based on artificialneural network[C]//Proceedings of the 7th International Conference on“Mathematical Methods in Reliability”:Theory,Methods,Applications.Beijing:Beijing Institute of Technology Press,2011:634-638
[6]Ku B Y,Thomas R J,Chiou C Y,et al.Power system dynamic load modeling using artificial neural networks[J].Power Systems,1994,9(4):1868-1874
[7]Heineman G T,Polloce G,Selkow S.Algorithms in a nutshell[M].California:O'Reilly Media,2008:226-250
[8]Cormen T H,Leiserson C E,Rivest R L,et al.Introduction to algorithms[M].2nd Edition.Boston:MIT Press and McGraw-Hill,2001:696-697
