面齿轮齿面的自适应采样方法

张 俐 丁志耀 王延忠

（北京航空航天大学 机械工程及自动化学院，北京 100191）

面齿轮齿面的自适应采样方法

张 俐 丁志耀 王延忠

（北京航空航天大学 机械工程及自动化学院，北京 100191）

面齿轮齿面的数字化是齿面检测的关键技术之一.针对在三坐标测量机上进行的齿面采样，提出一种根据给定精度确定采样网格点数量的方法:对采样网格边界线进行初步自适应，利用截平面法得到初始采样网格;同时根据给定的采样网格点数量，借助基于形状的采样算法，对初始采样网格进行迭代，生成自适应采样网格，最终实现面齿轮齿面数字化检测采样的自适应规划.

面齿轮齿面;采样网格;自适应

面齿轮传动是面齿轮与圆柱齿轮相啮合的新型齿轮传动，它是采用渐开线直齿轮刀具经展成加工而成.目前，国外有关研究机构已经设计出采用面齿轮传动的直升机主减速器，在体积小、重量轻、承载能力高、噪声低、可靠性高、寿命长、功率分流效果良好等方面显示了极大的优势，作为航空锥齿轮新的代表脱颖而出.因此，对面齿轮齿面进行检测，评定面齿轮的精度，显得尤为重要.而齿面数字化（即用离散的采样点提取齿面的原始形状信息）是齿面检测过程中的关键步骤.目前，在面齿轮齿面检测过程中，为了保证测量精度，通常采用缩小测量间距的方法，这就使测量效率显著降低，并增加了后续数据处理的工作量和难度.解决这一问题的有效方法是实现检测点的自适应分布，使检测点的分布随齿面曲率的变化而变化，即曲率越大，检测（采样）点越密，反之则越疏［1］.这样就能够比较真实地反映齿面的几何形状信息.基于此，在研究基于形状特征的已知齿面数字化基础上，本文对数字化齿面的自适应采样方法开展研究.

1 检测（采样）点数量的确定

确定合理的检测点数在齿面的数字化过程中具有重要的作用.检测点数过多不仅影响采样效率，而且有可能导致计算机内存溢出;但检测点数过少，则不能精确地描述齿面的几何特征.

目前对于检测点数的确定主要集中在规则曲面上，对自由曲面的研究比较少.文献［2］针对模型已知的自由曲面，对检测点的确定进行了比较详细的研究，将影响检测点数量的因素概括为2个:设计时给定的公差范围T和机床的加工能力P（一般取P=6σ）.假设加工误差服从正态分布:ε=N（0，σ2）.并给出了检测点数量的经验公式:

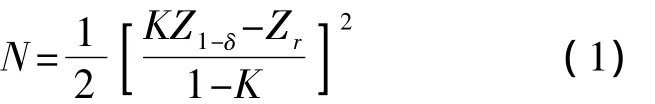
式中，K表示工艺能力系数，它是公差范围T和实际加工误差（分散范围6σ）之比，即K=T/6σ;Z1－δ表示标准正态概率分布的1－δ分位数;Zr表示标准正态概率分布的r分位数.

式（1）检测点数计算公式考虑了加工设备的工艺能力、检测的置信度和给定公差的大小，符合三坐标测量机（CMM，Coordinate Measuring Machine）检测的特点［3］，然而该公式未考虑曲面的面积因素，而且在K接近1时，检测样本将趋于无限大，因此在实际计算检测点时，还须根据自由曲面面积的大小对式（1）进行修正，以符合工程检测的特点.

基于此，针对面齿轮的齿面采样网格的划分，本文提出一种确定采样点数量的方法，思路如下:①确定齿面检测区域;②分别对横纵两边界线上的采样点进行初步自适应生成;③生成采样网格，确定采样点数量.

1.1 确定齿面检测区域

根据AGMA（美国制造商协会）2009-B01标准，齿顶和齿根的缩进量取为5%工作齿高（考虑到面齿轮齿根附近的过渡区，本文中将齿根缩进量取为10%工作齿高），内外端缩进量取为10%齿面宽.利用4个截平面确定的齿面检测区域如图1所示.

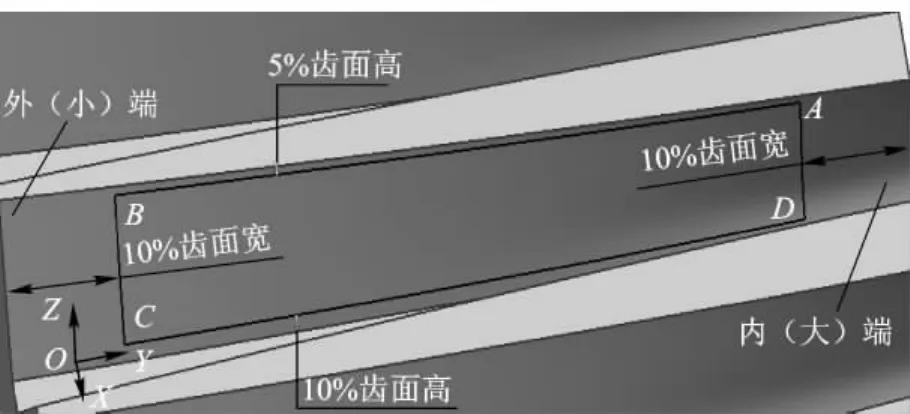
图1 齿面检测区域确定示意图

1.2 边界采样点初步自适应生成

采用文献［4－5］提出的基于曲面法曲率信息的算法，对图1中AB方向边界线及DA方向边界线进行采样点自适应生成.

面齿轮齿面方程［6］（工作面）如下:

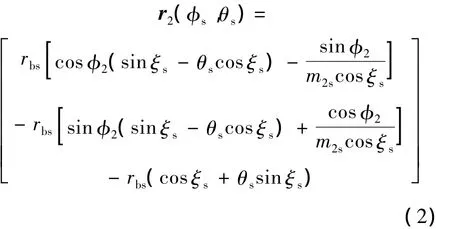
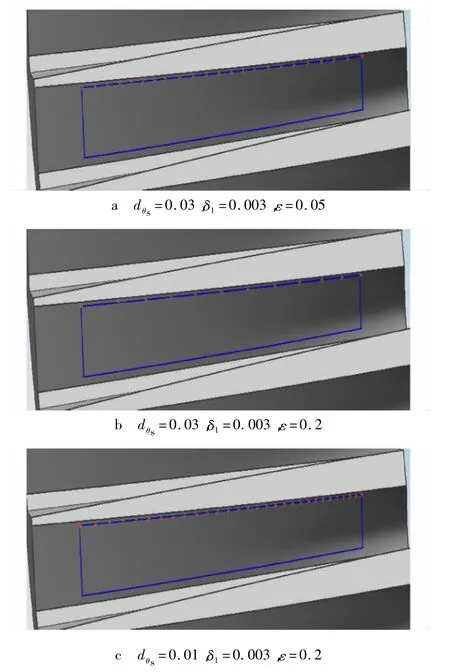
图2 采样结果

从3种采样结果的对比可看出:

1）当步长及反馈步长相同时，给定精度越小，采样点越多（更密），自适应效果减弱;

2）当给定精度及反馈步长相同时，步长越小，采样点越多，自适应效果减弱.

考虑到本文中所用面齿轮的尺寸很小，不宜使采样点过密，故不推荐使用过小的精度.图2b自适应效果较为明显，且采样点数比较合理，故本文采用其参数值:步长 dθs=0.03，反馈步长 δ1=0.003，给定精度 ε=0.2 mm.同理，纵向的各参数取值为:步长 dφs=0.006，反馈步长 δ2=0.000 6，给定精度同为0.2 mm.

根据上述要求遍历横纵2个方向的边界线，计算结果如图3所示.

图3 边界线自适应计算结果示意图

图3可见，横向边界线取了12个采样点，纵向边界线取了8个采样点，并且各采样点疏密程度有随曲率不同而变化的趋势.需要说明的是:为避免分区域（工作面-过渡面）求采样点，这里采用外端边界线CB而不是DA进行纵向初步自适应.

1.3 生成采样网格

根据1.2节的各采样点，利用与边界截面平行的截平面去截齿面，得到的初始采样网格如图4所示.

图4 初始采样网格示意图

由图4可确定齿面的采样点数量为96个（8×12网格）.图4中右下角的4个网格点处于过渡面区域内，它们的坐标需要利用面齿轮过渡面方程［6］重新计算.

2 自适应采样原理与算法

在给定了采样点数量之后，应研究如何尽可能真实地反映齿面的原始形状，即应对齿面采样点的分布规划进行研究.自适应采样方法［7］原理如下.

2.1 形状函数

该方法将“质心法”原理应用到曲面自适应采样.如图5所示，若质点m1和m3分别位于x轴上x1和x3处，则质点系的质心在x轴上的位置为

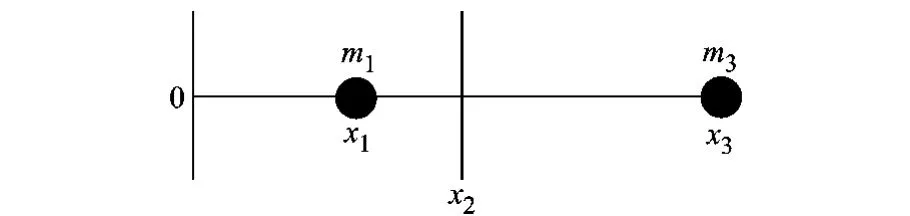
图5 质点系

将该原理应用于曲面测量中，以测点曲率代替质点质量，可以得到:

式中，∀i∈D，D={1，2，…，M}为物理域上采样点集合;ci=（ui，vi）T为参数域上采样点;r（c）为反映曲面局部曲率的形状函数;Ni为采样网格的邻域.

点p处任一方向的法曲率kn与主曲率k1和k2满足欧拉（Euler）公式:

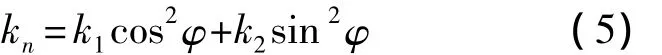
式中，φ为该方向与主曲率k1所在方向的夹角.由于主曲率k1和k2具有几何不变性，故将曲率测度定义为［8］

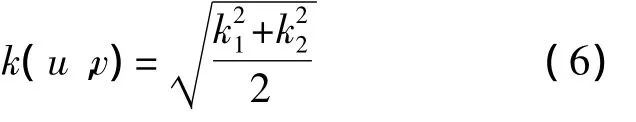
形状函数 r（c）取为［1］

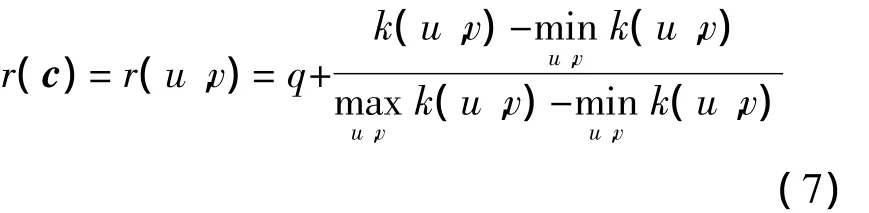
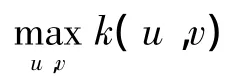
2.2 算法的实现

将式（4）改写为［9］

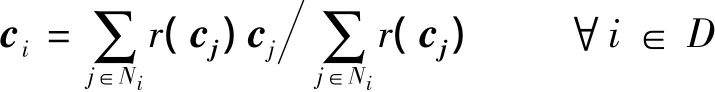
它可以通过如下迭代算法求解:

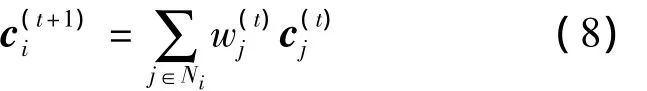
可见，ci等于它的邻域值加权之和.为充分反映迭代过程中网格的实时变化影响，在迭代循环过程中，ci要实时更新网格点的矢量，故式（8）改写成:

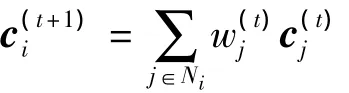
3 自适应迭代实例

在对齿面网格点进行迭代计算之前，应先设置边界条件.本文针对面齿轮齿面网格所设置的边界条件为:网格的4个角点保持不变，边界上的点只能沿所在边界方向变化.设置边界条件之后，需要确定邻域形式.图6描述了本文中所采用的邻域形式.可见，边界点（4个角点除外）采用二邻域形式，中间点采用四邻域形式.

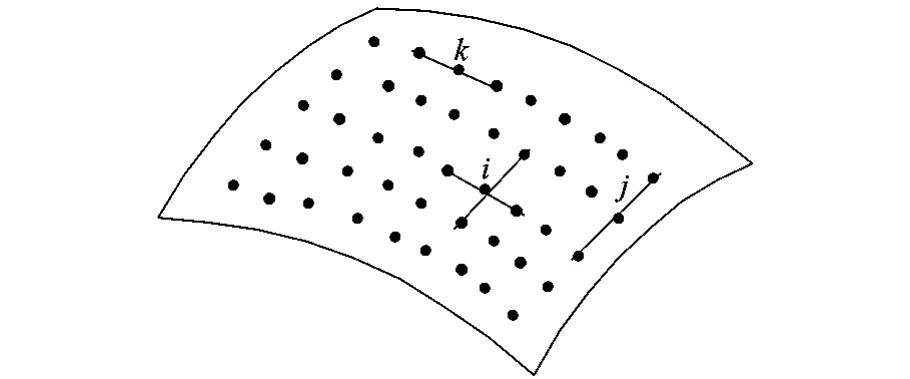
图6 采样点的邻域形式

根据形状函数的定义，可求得面齿轮齿面初始网格各点（图4）的形状函数r（ci），见表1.

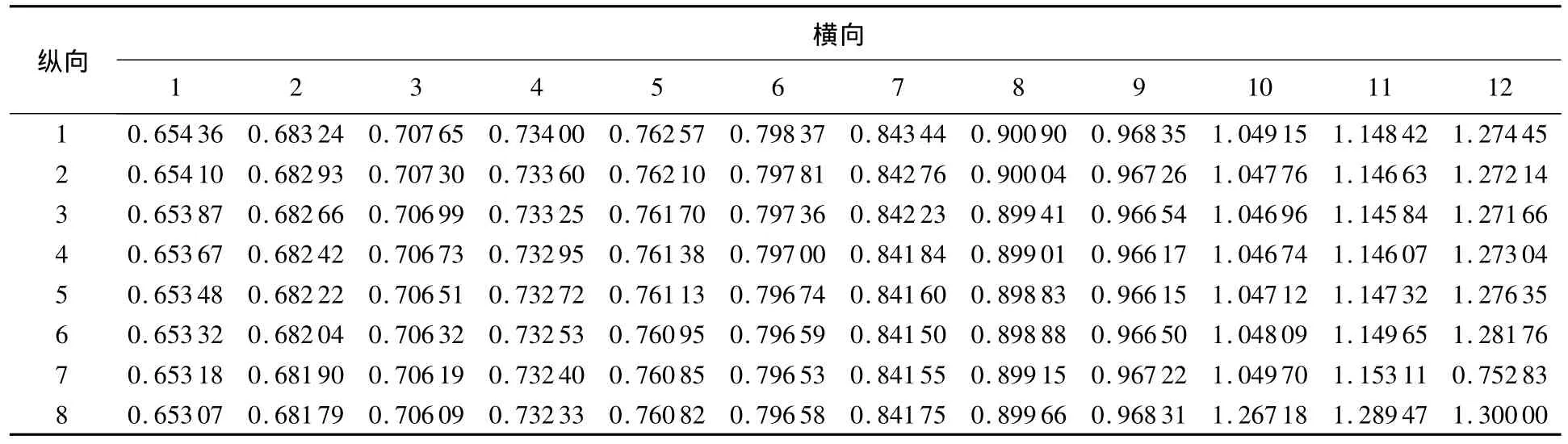
表1 初始网格点形状函数r（ci）值

表1可见齿面的变化趋势:由右至左（内端至外端），由上至下（齿顶至齿根），形状函数r（ci）依次变小，即曲率依次变小.需要注意的是:曲率主要变化方向是横向，纵向曲率变化不大.

图7为q=0.3时齿面自适应网格生成过程.

图7 齿面自适应网格的生成

可见，该算法具有自组织特征，采样点有向曲率大的区域（右下角）逐渐靠拢的趋势，采样的疏密依赖于齿面曲率.采用迭代100次后的自适应采样网格（图8），将尽可能充分地提取齿面的真实形状信息.

图8 迭代100次后的齿面采样点网格

4 结论

本文针对数学模型已知的面齿轮齿面，研究了提高采样精度和采样效率的齿面网格点自适应规划方法.首先提出一种确定采样点数量的方法:根据齿面法曲率信息对采样网格边界线进行初步自适应，生成边界采样点，之后利用截平面法得到初始采样网格;在给定了采样点数量之后，再根据质心概念推导出基于形状函数的采样算法，由迭代实例表明该算法具有如下优点:①极强的自组织能力;②网格采样点的疏密可根据齿面的曲率自行调整.基于该算法，可在给定采样点数条件下较合理地提取齿面形状信息，减小形状的采样失真，提高采样效率，从而实现面齿轮齿面数字化检测过程中采样的自适应规划.

（References）

［1］来新民，黄田.数学模型已知的自由曲面自适应采样［J］.计算机辅助设计与图形学学报，1999，11（4）:359－362

Lai Xinmin，Huang Tian.Adaptive sampling of digitizing for the known free-form surface［J］.Journal of Computer Aided Design and Computer Graphics，1999，11（4）:359－362（in Chinese）

［2］Menq Chiahsiang，Yan Hongtzong.Automated precision measurement of surface profile in CAD-direction inspection［J］.IEEE Transactions on Robotics and Automation，1992，8（2）:268－278

［3］Cho M W，Lee H，Yoon G S，at al.A feature-based inspection planning system for coordinate measuring machines［J］.International Journal of Advanced Manufacturing Technology，2005，26（9/10）:1078－1087

［4］李剑.自由曲面零件的寻位自适应检测方法研究［J］.仪器仪表学报，2002，23（5）:530－533

Li Jian.State searching adaptive measuring technique for freeform surface parts［J］.Chinese Journal of Scientific Instrument，2002，23（5）:530－533（in Chinese）

［5］任玉波，孙惠学.CAD模型已知的自由曲面在线检测方法研究［J］.精密制造与自动化，2006，3:15－17

Ren Yubo，Sun Huixue.Research on in-process inspection method for CAD model known free curved-surface［J］.Precise Manufacturing ＆ Automation，2006，3:15－17（in Chinese）

［6］朱如鹏.面齿轮传动的啮合特性研究［D］.南京:南京航空航天大学机电学院，2000

Zu Rupeng.Research on meshing characteristic of face gear drive［D］.Nanjing:College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，2000（in Chinese）

［7］Li S Z.Adaptive sampling and mesh generation［J］.Computer-Aided Design，1995，27（3）:235－240

［8］梅向明，黄敬之.微分几何［M］.北京:高等教育出版社，1981

Mei Xiangming，Huang Jingzhi.Differential geometry［M］.Beijing:Higher Education Press，1981（in Chinese）

［9］陈浪.基于三坐标测量机的曲面自适应采样和网格生成［J］.重庆大学学报:自然科学版，2001，24（4）:22－25

Chen Lang.Study on adaptive sampling and mesh generation of free-form surfaces based on coordinate measuring machine［J］.Journal of Chongqing University:Natural Science Edition，2001，24（4）:22－25（in Chinese）

Adaptive sampling method of face gear tooth surface

Zhang Li Ding Zhiyao Wang Yanzhong
（School of Mechanical Engineering and Automation，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

Digitizing of face gear tooth surface is one of the key technologies on the tooth surface measurement.Aiming at the sampling of tooth surface on CMM（coordinate measuring machine），a method to determine the quantity of the sampling mesh points according to given precision was presented.The boundary lines of sampling mesh were adapted firstly and the initial sampling mesh could be achieved by the method of cutting-planes.According to the given quantity of the sampling mesh points，there was iterative computation for the initial sampling mesh by the adaptive sampling algorithm based on the measure of curvature，and then the adaptive programming method of face gear tooth surface was developed.

face gear tooth surface;sampling mesh;adaption

TH 132.41

A

1001-5965（2012）02-0247-05

2010-09-30;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46;

CNKI:11-2625/V.20120221.1146.006

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.006.html

航空科学基金资助项目（20090451008）;国家自然科学基金资助项目（50875009）

张 俐（1961－），女，北京人，副教授，gracejune@buaa.edu.cn.

（编 辑:文丽芳）