网络计划中构建对偶网络模型的理论和方法

苏志雄 李星梅 乞建勋

（华北电力大学 经济与管理学院，北京 102206）

网络计划中构建对偶网络模型的理论和方法

苏志雄 李星梅 乞建勋

（华北电力大学 经济与管理学院，北京 102206）

针对现有的网络计划模型重点体现的不是其核心机动时间和路差，而是具体的时间和路长，进而使得该模型在运用时往往会遇到阻碍的问题，利用对偶原理，构建网络计划模型的对偶模型.首先，通过分析机动时间和路长之间的关系，推导出路差定理;其次，在路差定理的基础上，利用对偶原理构建对偶网络模型，并分析其性质;然后利用该模型揭示网络计划的对偶等价性;最后，通过例子进行验证和说明.该对偶网络模型重点体现了机动时间和路差，使得网络计划更具针对性和有效性.

运筹学;对偶理论;网络计划;时差

网络计划［1］产生于20世纪50年代，是目前最常用的处理项目计划的图形技术.机动时间（也称时差）和时间参数是其核心，对它们的研究伴随着网络计划的诞生而起步.在时间参数上，文献［2－3］修正了原有计算方法，使得同一工序系统即使对应不同的网络图也能得到唯一正确的时间参数.在机动时间上，国际当前通用的有总时差、安全时差、自由时差、节点时差和干扰时差［1，4］.文献［5］针对同一工序系统的不同网络图表示，对各时差计算方法进行了修正.针对其特性，国内外学者已经做了很多研究［6－10］，其成果已广泛应用于实践和求解各类经典问题.

网络计划是优化模型，用于求解优化问题，因此可以设想能否将优化理论运用到网络计划中.对偶理论是优化理论的基础，能够简化问题的求解，当前主要应用于多目标规划理论［11－12］.因而，可尝试运用对偶原理对网络计划模型进行研究，以达到模型改进的目的.网络计划模型需要改进的原因主要在于:首先，直接使用该模型往往不易顺利有效地解决相关问题，很多问题虽然求解目标与工期和路长相关，但求解过程中真正需要考虑的却是时差和路差.例如，文献［5，13］在等效化简时间-费用权衡问题时，需要考虑的仅仅是总时差和节点时差;文献［5，14］在求解k阶次关键路线问题时，也只需要分析自由时差和路差即可.其次，网络计划模型的根本价值在于时差，而非工期和路长，因此其特性主要是时差的特性.文献［5，15］分析了时差的动态特性;特别地，文献［5］分析了时差的静态特性，包括时差与路长的关系等，只与路差有关.但现有网络计划模型却重点反映工期和路长，进而在应用上，工期、路长等非实质因素常具干扰性，而时差、路差等实质因素的作用却被消弱，使得问题在求解上效果不佳.因此，需要构建重点反映时差和路差的新网络计划模型.

经上述分析，如果能构建新模型，使其既与网络计划模型之间满足对偶关系，又能充分体现时差和路差的关键作用，那么无疑更具优越性.在网络计划模型的改进上，人们长期主要针对应用范围对其进行拓广，从传统网络计划，如关键路线法和计划评审技术，拓广为随机网络计划［16］、模糊网络计划［17］、一般优先关系网络计划［18］、搭接网络计划［19］、流水网络计划［19］等，努力使得各类问题都能够用相应类型的网络计划表示.但是针对网络计划模型自身的转变，如初始-对偶转变，目前还缺乏相关研究.

本文通过分析时差、路差和路长的关系，运用对偶原理和最短路线法，构建网络计划模型的对偶网络模型，并分析该模型的性质.

1 网络计划的节点参数计算

任意网络计划图中，设Dij表示工序（i，j）的工期（duration），和分别表示节点（i）的最早时间参数（the earliest time）和最迟时间参数（the latest time），则和的计算方法如下.

1）从源点（1）开始:

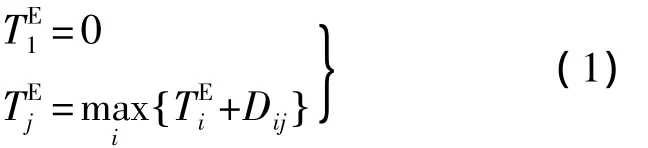
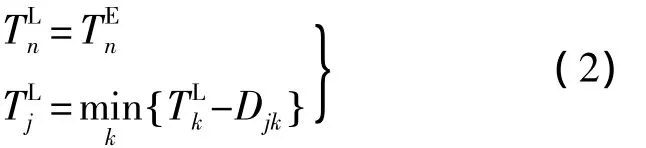
若（j）是虚出节点（紧后工序都是虚工序），（k）是（j）的紧后节点，则

2）从汇点（n）开始:

3）从源点（1）开始，若（j）是虚入节点（紧前工序都是虚工序），（i）是（）j的紧前节点，则

2 基本概念

总时差（total float）.工序i，（j）的总时差是指在不影响工程总工期的条件下，该工序可以使用的机动时间的最大值，用表示，即

安全时差（safety float）.工序i，（j）的安全时差是指该工序的紧前工序在最迟结束时间结束时，该工序仍可以使用而不影响工程总工期的机动时间的最大值，用表示，即

自由时差（free float）.工序i，（j）的自由时差是指在不影响紧后工序最早开始的前提下，该工序可以使用的机动时间的最大值，用表示，即

干扰时差（interference float）.如果工序的干扰时差为正，表示当该工序的紧后工序能够最早开始，并且紧前工序能够最迟结束的情况下，它工期可以延长的最大时间;如果该时差为负，其绝对值表示当该工序的紧后工序能够最早开始，并且紧前工序能够最迟结束的情况下，它的工期需要缩短的最小时间.工序i，（）j的干扰时差用表示，即

节点时差（node float）.节点（i）的时差是指该节点的最迟时间与最早时间的差值，记为，即

路差.从源点到汇点的路线μ的路差表示该路线与关键路线μ▽的路长之差，记为，即

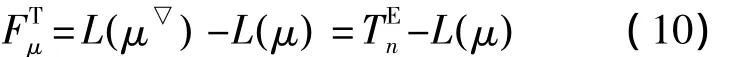
3 路差定理

网络计划图中任意路线μ的路差可用该路线上工序和节点的时差表示，表现为以下公式:

证明 设网络计划图中任意路线μ为

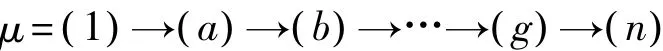
对于任意工序 （i，j），根据式（5）～式（8）:

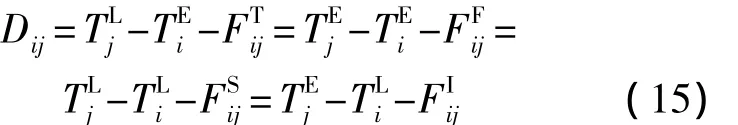
1）根据路长的概念和式（15）:

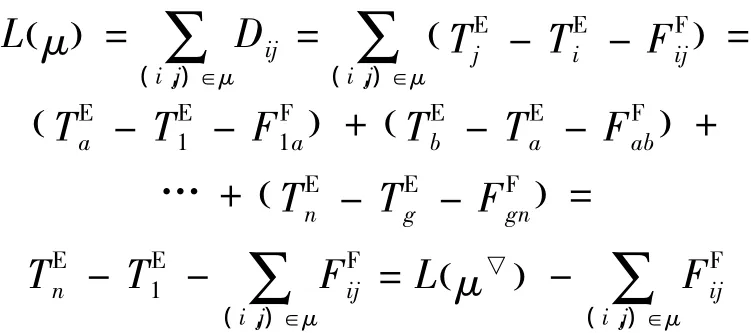
根据式（10）:

式（11）成立.

2）同理可证式（12）成立.

3）根据路长的概念和式（15），以及前面式（11）和式（12）的推导过程:

根据式（1）、式（2），源汇点时差为零，所以

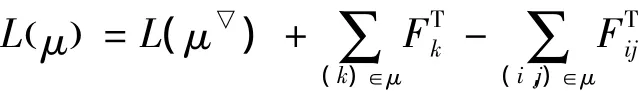
根据式（10）:

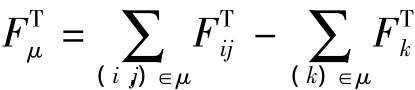
式（13）成立.

4）同理可证式（14）成立. 证毕

4 对偶网络模型及构建方法

4.1 对偶网络模型的概念和构建原理

根据对偶的含义，对于一个网络计划模型，记为A，如果基于A能够生成另一个网络模型，记为B，使其具有与A相同的结构和性质，但表示方法却与A相反.例如，根据文献［5］，A中参数反映的是最长路的情况，那么B中参数反映的就是最短路的情况，并且这2种路线表示的是相同的路线，那么就称B是A的对偶网络模型.

根据路差的概念，如果路线的路长越大，那么它的路差就越小，反之亦然.这样，任意路线的路长和路差就具有了对偶关系，可以在路差的基础上构建网络计划模型的对偶网络模型.

根据路差定理，任意路线的路差可由不同时差用不同的4种方式组成，因此可以利用这4种方式构建4类网络模型.首先，将每个时差的正值或负值都作为模型中对应工序的工期，使模型中任意路线的路长都等于原网络计划中对应路线的路差;然后，用最短路线法计算各节点的参数，使得任意节点参数对应的最短路就是原网络计划中相应节点参数对应的最长路.在这里，找最短路等同于在原网络计划中找最长路，这样就可以构建出原网络计划模型的对偶模型.

通过上述分析，由一个网络计划模型可以构建出4个不同的对偶网络模型，它们综合反映同一个网络计划模型的各种性质，相互具有互补性.因此，可称它们为互补对偶网络模型.

4.2 对偶网络模型的构建方法

4.2.1 最短路网络模型

文献［20］给出了最短路网络模型中节点参数的计算方法:

1）先从源点（1）开始

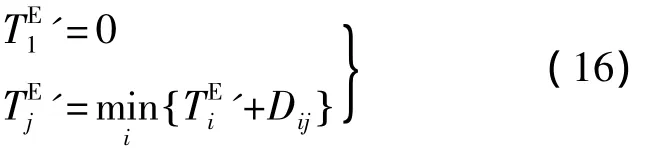
2）再从汇点（n）开始

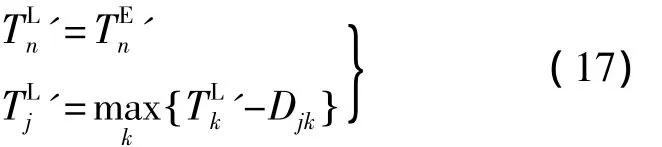
若（j）是虚出节点，（k）是（j）的紧后节点，则

3）再从源点（1）开始，若（j）是虚入节点，（i）是（j）的紧前节点，则

4.2.2 第一类对偶网络模型的构建方法及性质

第一类对偶网络模型是基于式（11）构建的，其构建方法如下:

1）计算工序的自由时差;

2）用工序的自由时差代替工期，并用式（16）～式（19）计算节点参数.

根据最短路模型和文献［5］自由时差特性，该类对偶模型的基本性质是:

1）所有节点的参数TE'=0，TL'≤0;

2）源点到任意节点的最短路长度为零;

3）最短路线上所有节点的参数TL'=0.

4.2.3 第二类对偶网络模型的构建方法及性质

第二类对偶网络模型是基于式（12）构建的，其构建方法如下:

1）计算工序的安全时差;

2）用工序的安全时差代替工期，并用式（16）～式（19）计算节点参数.

根据最短路模型和文献［5］安全时差特性理论，该类对偶模型的基本性质是:

1）所有节点的参数TE'≥0，TL'=0;

2）任意节点到汇点的最短路长度为零;

3）最短路线上所有节点的参数TE'=0.

4.2.4 第三类对偶网络模型的构建方法及性质

第三类对偶网络模型是基于式（13）构建的.由于需要将节点时差表示为该类对偶网络模型中路长的一部分，故在构建该类对偶网络模型时需将节点表示成工序的形式，即（i）表示成i，（i'），该工序称为辅助工序.

该类对偶网络模型的构建方法如下:

1）计算工序的总时差，并代替各自工期;

2）计算节点的节点时差;

3）将除源点和汇点以外的各节点（i）都表示成辅助工序i，（i'），其工期设为－;

4）用式（16）～式（19）计算节点参数.

根据最短路模型，该类模型的基本性质是:最短路长度为零，其上所有节点参数为零.

4.2.5 第四类对偶网络模型的构建方法及性质

第四类对偶网络模型是基于式（14）构建的.与4.2.4同理，在构建该类对偶网络模型时需将除源点和汇点以外的节点表示成辅助工序.

该类对偶网络模型的构建方法如下:

1）计算工序干扰时差，并代替各自工期;2）计算节点的节点时差;

3）将除源点和汇点以外的各节点（i）都表示为辅助工序i，（i'），其工期设为;

4）用式（16）～式（19）计算节点参数.

第四类与第三类对偶模型的基本性质相同.

4.3 对偶等价性

接下来分析不同网络计划图的对偶网络模型之间的关系.这里所说的不同网络计划图指的是相互之间工序工期以及总工期不同，但要求网络的结构相同，即工序的数量和相互之间的逻辑关系相同，否则，不同结构的网络计划图对应的对偶网络的结构也必然不同，从而没有可比性.

根据文献［5］可知，网络计划中的各类时差都可以用路差表示.不同的网络计划之间，虽然工期不同，对应的路线长度也不同，但对应的不同路线的路长之差却有可能相同，就如同“8≠5，4≠1，但8－5=4－1”一样.因此，如果不同网络之间对应的路差相同，则网络中对应的工序和节点的时差也相同，那么根据对偶网络模型的构建方法，它们的对偶网络模型也相同.简单地说就是，不同的网络计划可能有相同的时差和对偶网络，一个对偶网络的原网络计划有无穷多个.

但是反过来说，对于同类型的不同对偶网络，说明各自的原网络计划之间对应的时差不同，即路差也不同，那么对应的路长必有不同，就如同“若 a－b≠c－d，那么必然有 a≠c或b≠d”一样，进而对应工序的工期必然也有不同，则对应的网络计划也必然不同.因此，同类型的不同对偶网络对应的原网络计划必然不同.

通过上述分析可知，对偶网络模型具有原网络计划模型所不具备的特性，能够反映不同网络计划之间的关系.从这个意义上说，具有相同对偶网络的所有网络计划之间具有某种等价性，可称之为对偶等价性.该性质表明，通过研究一类或几类互补对偶网络，就能够获得与这些对偶网络相对应的无穷多个原网络计划的共同特性.

5 应用举例

构建如图1所示的网络计划模型的对偶网络模型.

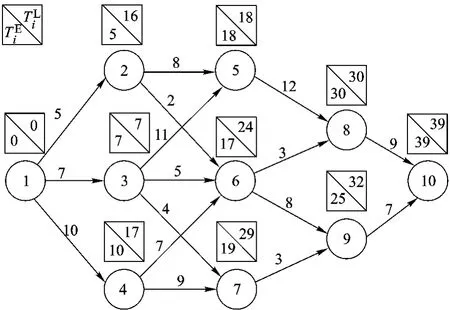
图1 网络计划图

分别构建该模型的4类对偶网络模型.

1）构建第一类对偶网络模型.①计算各工序的自由时差;②用各工序的自由时差代替工期，并用式（16）～式（19）计算节点参数，得图2.

图2是图1的第一类对偶网络模型.

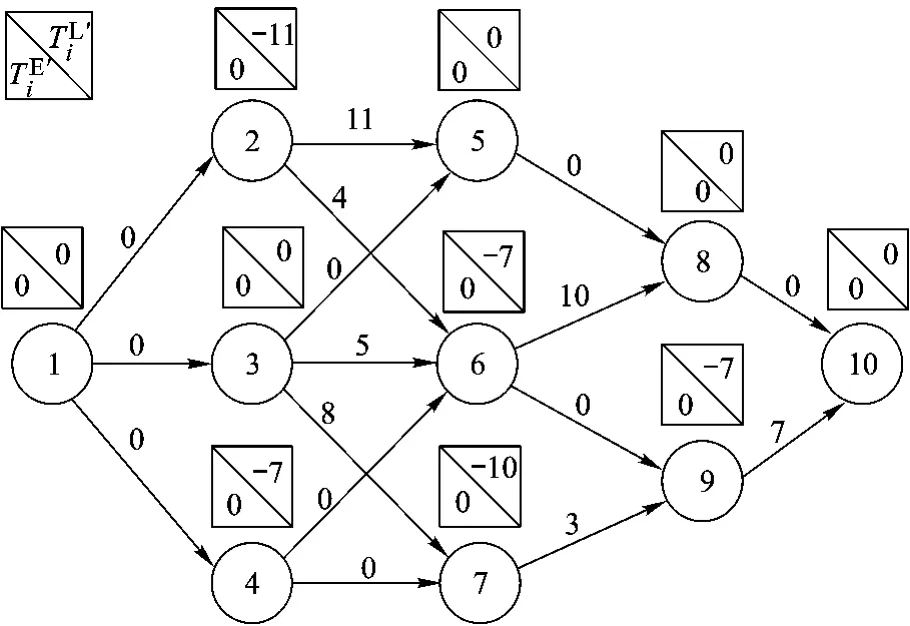
图2 第一类对偶网络模型

2）构建第二类对偶网络模型.①计算各工序的安全时差;②用工序的安全时差代替工期，并用式（16）～式（19）计算节点参数，得图3.

图3是图1的第二类对偶网络模型.

图3 第二类对偶网络模型

3）构建第三类对偶网络模型.①计算各工序总时差，并代替各自工期;②计算各节点的节点时差;③将除源点（1）和汇点（10）以外的各节点（i）都表示成辅助工序（i，i'），其工期设为－;④用式（16）～式（19）计算参数，得图4.

图4是图1的第三类对偶网络模型.

4）构建第四类对偶网络模型.①计算工序干扰时差，并代替各自工期;②计算各节点的节点时差;③将除源点（1）和汇点（10）以外各节点（i）都表示成辅助工序i，（i'），其工期设为;④用式（16）～式（19）计算参数，得图5.

图5是图1的第四类对偶网络模型.

可以验证，图2～图5中的各类最短路均表示图1中的各类最长路，由节点参数TE'=TL'=0的节点连接而成的路线就是最短路线，其长度均为零，都对应于图1中的最长路线，即关键路线.

图4 第三类对偶网络模型

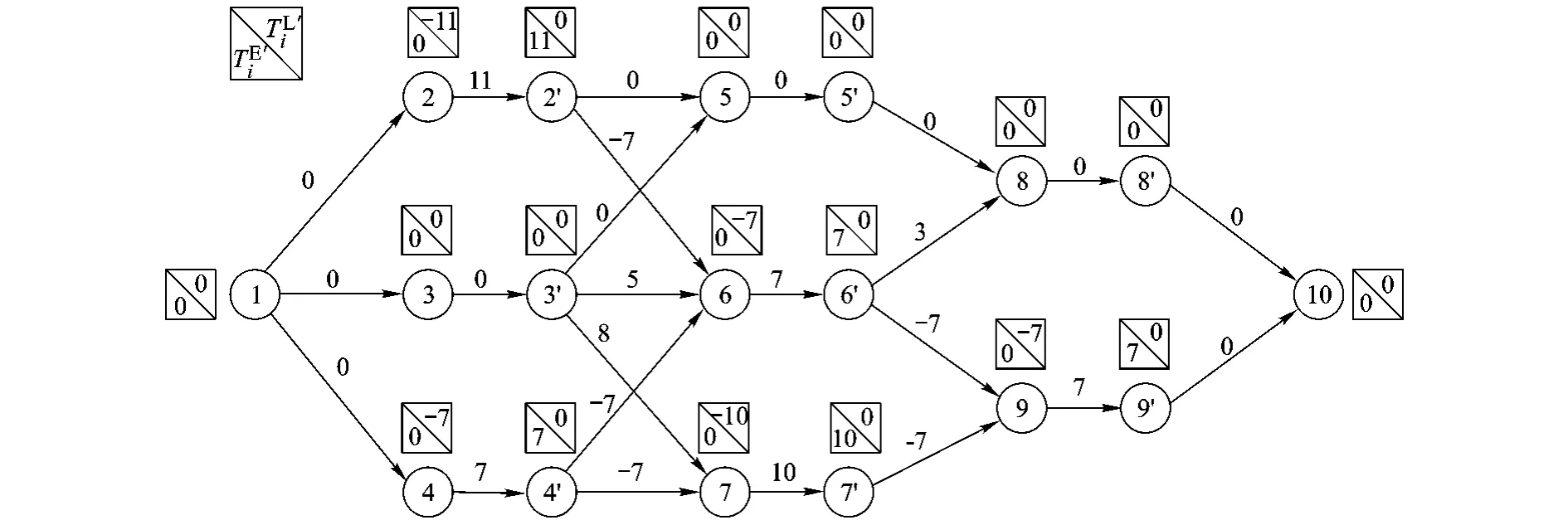
图5 第四类对偶网络模型

6 结论

本文通过分析路长与时差之间的关系，构建出网络计划模型的对偶网络模型.该模型既满足了与原网络计划模型之间对偶关系，又充分体现了时差和路差的关键性作用，与网络计划模型相比更具优越性.两模型之间的关系是，一个网络计划模型对应有4类对偶网络模型，而一个对偶网络模型对应有无穷多个网络计划模型.此外，利用该模型，还揭示了网络计划模型的对偶等价性，通过研究一个对偶网络模型就能够得到与其对应的无穷多个网络计划模型的共同性质，为网络计划优化的进一步深入提供了思想和依据.

（References）

［1］Demeulemeester E L，Herrlelen W S.Project scheduling［M］.Boston:Kluwer Academic Publishers，2002:17－48

［2］Michael D J，Kamburowski J，Stallman M.On minimum dummy arc problem［J］.Operations Research，1993，27（2）:153－168

［3］Elmaghraby S E，Kamburowski J.On project representationand activity floats［J］.Arabian Journal of Science and Engineering，1990，15:627－637

［4］Elmaghraby S E.Activity nets:a guided tour through some recent developments［J］.European Journal of Operational Research，1995，82:383－408

［5］王强，李星梅，乞建勋.双代号网络图中虚工序对时差计算公式的影响与修正［J］.系统工程理论与实践，2008（6）:106－114

Wang Qiang，Li Xingmei，Qi Jianxun.A research on the influence of dummy activity on float in an AOA networkand its amendments［J］.Systems Engineering-Theory ＆ Practice，2008（6）:106－114（in Chinese）

［6］乞建勋，张立辉，李星梅.网络计划管理中的机动时间特性及其应用［M］.北京:科学出版社，2009:22－45

Qi Jianxun，Zhang Lihui，Li Xingmei.Property and application of float in network planning management［M］.Beijing:Science Publisher，2009:22－45（in Chinese）

［7］王佳，李星梅，乞建勋.基于机动时间的平行序链顺序优化算法设计［J］.系统工程学报，2008，23（4）:455－461

Wang Jia，Li Xingmei，Qi Jianxun.Sequencing optimalarithmetic design of parallel procedure chains basedon activity float［J］.Journal of Systems Engineering，2008，23（4）:455－461（in Chinese）

［8］Yakhchali S H，Ghodsypour S H.Computing latest starting times of activities in interval-valued networks with minimal time lags［J］.European Journal of Operational Research，2010，200（3）:874－880

［9］Sirakoulis K K.The effectiveness of resource leveling tools for resource constraint project scheduling problem［J］.International Journal of Project Management，2009，27（5）:493－500

［10］Karaca Z，Onargan T.The application of critical path method（CPM）in workflow schema of marble processing plants［J］.Materials and Manufacturing Processes，2007，22（1）:37－44

［11］Rodder W.A generalized saddlepoint theory:its application to duality theory for linear vector optimum problems［J］.European Journal of Operational Researh，1977，1（1）:55－59

［12］Ivanov E H，Nehse R.Some results on dual vector optimization problems［J］.Optimization，1985，16（4）:505－517

［13］乞建勋，李星梅，王强.等效子网络的理论与方法［J］.管理科学学报，2010，13（1）:40－44

Qi Jianxun，Li Xingmei，Wang Qiang.Theories and methods of creating equivalent sub-network［J］.Journal of Management Sciences in China，2010，13（1）:40－44（in Chinese）

［14］李星梅，乞建勋，苏志雄.自由时差定理与k阶次关键路线的求法［J］.管理科学学报，2009，12（2）:98－104

Li Xingmei，Qi Jianxun，Su Zhixiong.Free float theorem and algorithm of seeking the k-th order critical path［J］.Journal of Management Sciences in China，2009，12（2）:98－104（in Chinese）

［15］李星梅，乞建勋，苏志雄.双代号网络计划中工序机动时间蔓延性研究［J］.系统工程学报，2009，24（1）:39－45

Li Xingmei，Qi Jianxun，Su Zhixiong.Study of activity float spread property in activity-on-arc network planning［J］.Journal of Systems Engineering，2009，24（1）:39－45（in Chinese）

［16］王众托，张军.网络计划技术［M］.沈阳:辽宁出版社，1984

Wang Zhongtuo，Zhang Jun.Network planning technology［M］.Shenyang:Liaoning Publisher，1984（in Chinese）

［17］张连营，王亮，吕文学.网络计划的模糊分析［J］.天津大学学报，2004，37（2）:175－178

Zhang Lianying，Wang Liang，Lü Wenxue.Calculation and analysis of project network based on fuzzy set［J］.Journal of Tianjin University，2004，37（2）:175－178（in Chinese）

［18］Elmaghraby S E，Kamburowski J.The analysis of activity networks under generalized precedence relations（GPRs）［J］.Management Science，1992，38（9）:1245－1263

［19］杨冰.网络计划计算模型的统一［J］.系统工程理论与实践，2002（3）:51－55

Yang Bing.Unifyingcalculatingmodelsforthe network Planning［J］.Systems Engineering-Theory ＆ Practice，2002（3）:51－55（in Chinese）

［20］苏志雄，李星梅，乞建勋.基于CPM原理和Dijkstra算法的SPM网络计划模型及性质［J］.运筹与管理，2008，17（1）:148－153

Su Zhixiong，Li Xingmei，Qi Jianxun.SPM network planning model and its characteristics based on CPM theory and Dijkstra algorithm［J］.Operations Research and Management Science，2008，17（1）:148－153（in Chinese）

Theory and method of creating dual network model in network planning

Su Zhixiong Li Xingmei Qi Jianxun

（School of Business Administration，North China Electric Power University，Beijing 102206，China）

Aiming at problem that existing network planning model incarnates specific time and path length prominently instead of its core float and path length difference，which makes obstacles common exist when using the model in practice，dual model of network planning model was founded by using dual theory.Firstly，path length theorem was deduced by analyzing relation between float and path length;Secondly，based on path length theorem，dual network model was founded by using dual theory，and its properties were analyzed;Thirdly，dual equivalence property of network planning was revealed by using the model;Finally，the model was validated and illuminated by illustration.The dual network model incarnates float and path length difference prominently，which makes network planning have more prominent pertinence and validity.

operational research;dual theory;network planning;float

TB 114.1

A

1001-5965（2012）02-0257-06

2010-11-19;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:46;

CNKI:11-2625/V.20120221.1146.013

www.cnki.net/kcms/detail/11.2625.V.20120221.1146.013.html

国家自然科学基金资助项目（70671040）;华北电力大学博士研究生创新基金资助项目

苏志雄（1983－），男，山西朔州人，博士生，suzhixiongbaner@126.com.

（编 辑:文丽芳）