基于SA湍流模型的DES方法应用

陈江涛 张培红 周乃春 邓有奇

(中国空气动力研究与发展中心，绵阳621000)

20世纪60年代，计算流体力学 (CFD，Computational Fluid Dynamics)开始初步应用于飞行器设计.随着计算机技术的迅猛发展，CFD技术取得了巨大的进步，解决复杂工程问题的能力迅速增强.而今，CFD已经成为空气动力学研究的最重要手段之一，在飞行器设计等诸多工业领域里发挥了重要作用.目前，工程中多采用雷诺平均 N-S方程 (RANS，Reynolds-Averaged Navier-Stokes)的方法，该方法计算时间短、可靠性高，在工程界得到了广泛的应用.然而对于分离流动的计算，RANS方法往往不能给出不同尺度涡的发展变化细节.以当前的计算机水平，大涡模拟 (LES，Large Eddy Simulation)和直接数值模拟在复杂外形和高雷诺数 (大于105)问题中巨大的计算量使得这些高级模拟方法难以在工程中广泛应用.

1997 年 Spalart［1］发展的分离涡模拟 (DES，Detached-Eddy Simulation)方法使得模拟实际工程问题中大范围分离流动有了现实可行性，被认为是在现有的大型计算机集群的水平下，解决高雷诺数大分离非定常流动模拟最有可能成功的方法.DES把LES和RANS两种方法的优点相结合，是一种利用单一湍流模式的三维非定常数值求解方法，该湍流模式在网格足够密的地方相当于LES中的亚格子应力模式，在其他地方相当于RANS模式［2］.与 LES相比，DES方法不考虑湍流附面层内大量小尺度脉动运动，所需的网格数量大大降低，这样既可以在附面层内发挥RANS方法计算量小的优势，又可以在流动分离区域，对大尺度的脱体分离涡进行较好的模拟，既能捕捉到分离流动的主要特性而又相对经济.

本文使用基于SA(Spalart-Allmaras)湍流模型的DES方法，对圆柱绕流和超声速圆柱底部流动等高雷诺数大分离湍流进行了数值模拟，对分离区主要湍流结构的捕捉和平均压力的预测取得了满意的结果.

1 基于SA模型的DES方法

SA一方程模型［3］是由 Baldwin-Barth湍流模型发展而来的，方程的形式和系数通过量纲分析、伽利略不变性分析和实验结果验证得到.实验结果包括二维混合层、尾迹流动和平板边界层结果.

该模型的提出是为了改善代数混合长度模型模拟的结果，发展适用于复杂流动模拟的当地模型，提供比两方程湍流模型更简单的模型.

在方程中使用了到壁面的最近距离.SA模型的应变量 ν～在近壁处与离壁面的距离有线性变化关系，所以使用SA一方程湍流模型时在壁面附近不需要非常精细的网格，只需与代数湍流模型相当的网格即可，因而也具有计算容易的优点，对简单流动有着良好的收敛速度.

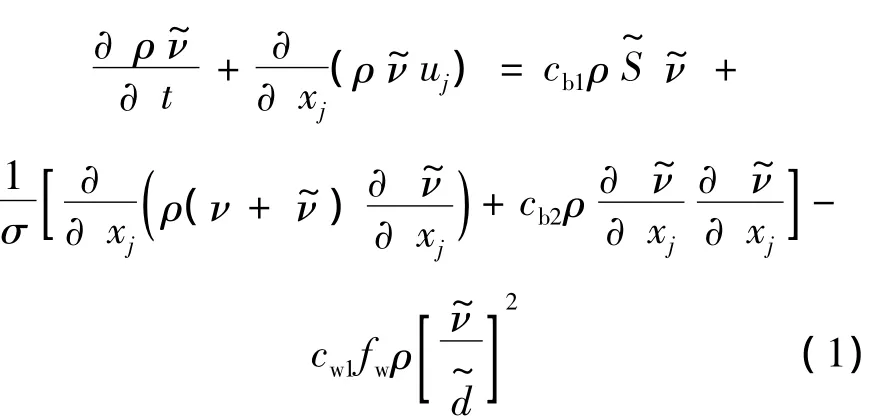
式 (1)的右端分别为涡流粘性的生成项、扩散项 (包括守恒扩散和非守恒扩散)和壁面破坏项.各系数的取值如下:

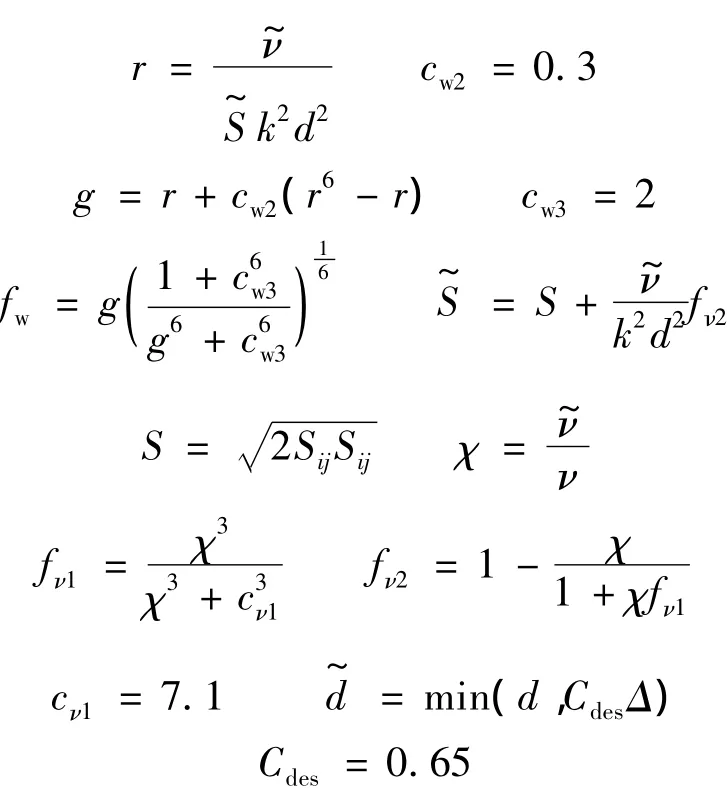
其中，d是流场中某位置到最近壁面的距离;Δ是LES方法中的滤波尺度.在物面附近有d＜CdesΔ，于是=d，此时的DES方法与SA湍流模式一致.随着d的逐渐变大，当d＞CdesΔ时，有=CdesΔ，此时湍流涡粘系数的衰减便由当地的网格尺度来确定.由式 (1)可见，当右端第1项即生成项和最后一项即衰减项达到平衡时，即

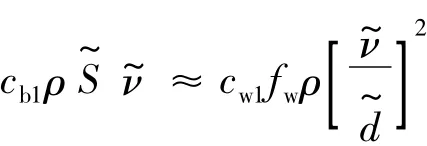
2 大分离湍流模拟应用

本文使用有限体积法求解N-S方程和湍流模型方程，使用分段线性插值重构单元内物理量的分布，空间精度为2阶，使用Roe格式计算无粘通量.时间推进使用双时间步LUSGS方法，时间精度同样为2阶.

2.1 超声速圆柱底部流动

超声速圆柱底部流动［4］存在分离旋涡、膨胀波、激波等复杂流动现象.在圆柱底部，流动急剧膨胀产生分离，形成主回流区.在底部下游，外部无粘流动与主回流区之间存在自由剪切层.当自由剪切层在对称轴相交时，流动通过再压缩与来流最终保持一致.底部受膨胀波的影响压力较低，是底部阻力产生的原因.传统的RANS模拟无法精确模拟底部压力，是导致难以准确预测飞行器阻力的一个重要原因.

算例中自由来流的条件是:Ma∞=2.46，单位雷诺数 Re/L=45 ×106m－1，T∞=145 K，P∞=31415Pa.圆柱半径R=31.75mm.图1给出了计算域的大小.圆柱长为8R，计算域出口离底部距离为10R，侧向计算域离圆柱表面距离为4.15R.

图2给出了子午面上网格分布.在近壁面和尾流区内都进行了加密，轴向网格点为250，周向网格点为140，径向网格在圆柱段和尾流区分别为120和220，离开壁面的第1层网格距离壁面0.0001R，总网格量是620万.

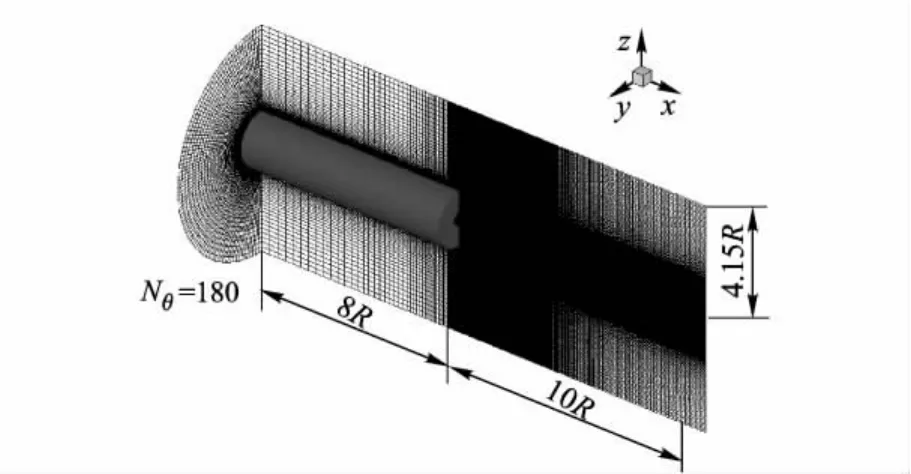
图1 超声速圆柱底部流动计算域示意图

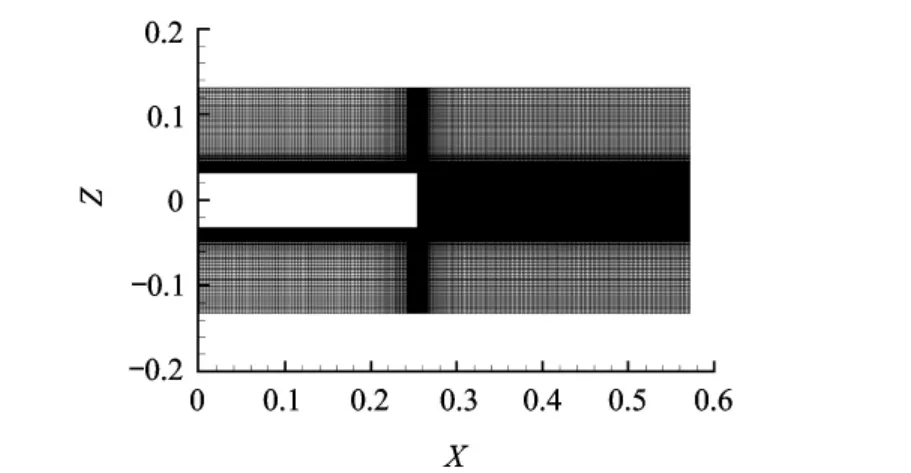
图2 超声速圆柱计算网格

计算中使用的同一时间步长Δt=3×10－7s，用圆柱半径和自由来流速度无量纲化可得Δt*=ΔtU∞/R=5.6×10－3.进出口和周向远场均使用了基于特征关系的远场边界条件，壁面使用无滑移绝热边界条件.

图3和图4分别给出了子午面上瞬时马赫数和瞬时密度梯度幅值|Δρ|的云图分布，对圆柱末端拐角处的膨胀波和对称轴处的激波都分辨得比较清楚，捕捉到了自由剪切层内的湍流涡结构，对于尾流区内的剪切层涡结构的分辨率不够理想.

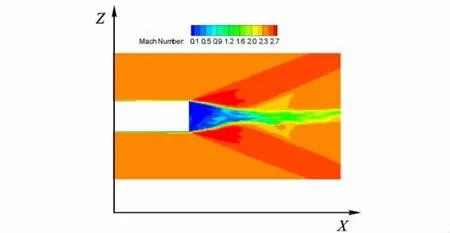
图3 底部流动子午面马赫数云图

图4 底部流动子午面密度梯度幅值的云图

图5 底部流动Q值的等值面 (使用马赫数云图着色)

图5 给出了使用 Q(Q= －1/2ui，juj，i)判据［5］来识别流场的涡结构 (使用马赫数的云图着色)，从瞬时流场形态可以清楚地看出，底部后存在着丰富的涡结构.

图6给出了圆柱底部的平均压力分布.可见，相对于RANS模拟，DES得到的平均压力分布跟实验值吻合得更好，基本上捕捉到了沿径向保持不变的压力分布趋势.说明采用本文方法能准确预测底部压力分布.

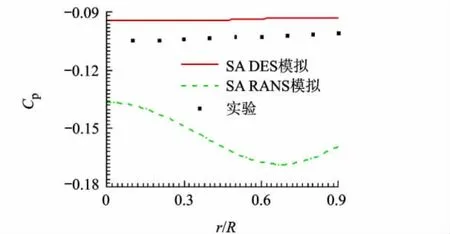
图6 底部平均压力分布

2.2圆柱绕流模拟

高雷诺数圆柱绕流是检验程序非定常模拟的很好算例，有大量实验结果可以进行验证.来流的马赫数为0.2，雷诺数ReD=1.40×105.在该雷诺数下，流动属于亚临界流动，非常接近临界雷诺数.在计算过程中，假定附体边界层内为全湍流，避免了转捩的问题，此时流动的现象和超临界流动一致，因此将数值模拟的结果和超临界流动实验结果进行对比，而不是同一雷诺数的实验结果.计算中使用全局统一物理时间步长t=0.000005 s，大约相当于每个涡脱落周期内有110个真实物理时间推进步.

展向计算域取为LY=4D(D为圆柱直径)，布置了50个网格点，使用对称边界条件.远场离圆柱表面距离为20D，径向布置了120个网格点，使用基于特征关系的远场边界条件.壁面使用无滑移绝热边界条件，周向布置了160个网格点.网格总量为96万.展向切面网格和壁面网格见图7.在边界层和尾流区内进行了加密，离开壁面的第1层网格距壁面的距离为5.0×10－5D，无量纲距离为0.17.

图7 圆柱展向截面网格和壁面网格

分别使用SA URANS(Unsteady RANS)和SA DES对圆柱绕流进行了模拟.图8和图9展示了同一个瞬时，使用同样的Q值识别的流场涡结构.可以清楚地看到SA DES成功地呈现了流动在圆柱被风面的分离，在尾流区出现上下交替变化的涡街结构，并且在展向呈现变化.而SA URANS虽然在圆柱被风面有分离现象，但是尾流区的涡结构大部分被抹掉，而且在展向分布一致.说明了URANS方法抑制了三维非定常涡结构的形成.

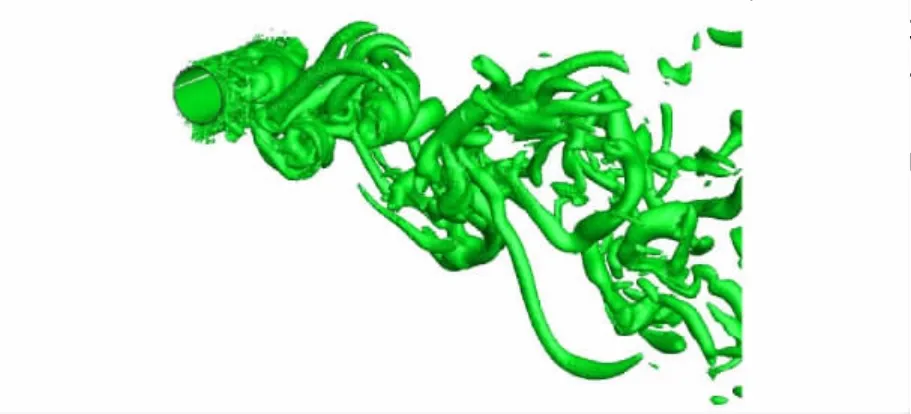
图8 圆柱尾流区的涡结构 (SA DES)

图10和图11展示了同一个瞬时，在展向平面上涡量的云图.从图中可以清楚地看到SA DES能够形象地展示尾流区的涡街结构，而SA URANS抹掉了大部分分离区的涡结构.

图9 圆柱分离区和尾流区的涡结构 (SA URANS)

图10 圆柱尾流区的涡量云图 (SA DES)

图11 圆柱尾流区的涡量云图 (SA URANS)

表1给出了计算得到的平均阻力系数、平均背压系数和Strouhal数Sr.实验所得雷诺数是3.5×106＜Re＜8.4×106.表1可见，使用SA DES模拟得到的定量结果跟实验值吻合得较好.其中平均阻力系数完全落在实验结果的上下限之内，平均背压系数和Sr数与实验吻合得很好.

表1 圆柱平均阻力系数、背压系数和Sr数

图12展示了圆柱表面平均压力分布，其中方位角θ从圆柱前缘驻点开始算起.Roshko实验［6］是 ReD=8.4 ×106的实验结果，Van Nunen实验［7］是 ReD=7.6×106的实验结果，这2组实验都是超临界流动.可见，使用SA DES模拟得到的结果完全落在这2组实验结果之内，说明对平均压力分布的预测是令人满意的.

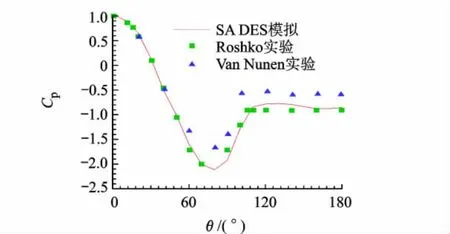
图12 圆柱表面平均压力分布

3 结论

1)DES能较为清晰地捕捉分离区内的主要流动结构，而RANS模拟因为模型本身耗散过大的原因，分离区的大部分湍流涡结构都被抹平.

2)圆柱和底部的平均压力分布的预测与实验值吻合较好，验证了DES方法在大分离湍流模拟中的应用前景.

References)

［1］Spalart P R.Strategies for turbulence modeling and simulations［J］.Int J Heat Fluid Flow，2000，21:252－263

［2］Travin A，Shur M，Strelets M，et al.Detached-eddy simulations past a circular cylinder ［J］.Flow Turbul Combust，2000，63:293－313

［3］Spalart P R，Allmaras S R.One-equation turbulence model for aerodynamic flows［J］.Recherche Aerospatiale，1994(1):5－21

［4］Simon F，Deck S，Guillen P，et al.RANS-LES simulations of supersonic base flow［C］//44th AIAA Aerospace Sciences Meeting.Reston:American Institute of Aeronautics and Astronautics Inc，2006:10723－10742

［5］Hunt J C R，Wray A A，Moin P.Eddies，stream and convergence zones in turbulent flows［R］.Center for Turbulence Research Report CTR-S88，1988

［6］Roshko A.Experiments on the flow past a circular cylinder at very high Reynolds number ［J］.Journal of Fluid Mechanics，1961，10(3):345－356

［7］Van Nunen.Pressure and forces on a circular cylinder in a cross flow at high Reynolds number［C］//Flow Induced Structural Vibrations.Berlin:Springer-Verlag，1974:748 －754