相角裕度和幅值裕度的一种估算方法
2012-06-21刘美侠孙延永
刘美侠,孙延永
(宿迁学院机电工程系,江苏 宿迁 223800)
控制系统的稳定性是系统分析和设计所需解决的首要问题。在实际系统中,动态稳定性不仅必须保证,而且还要有一定的稳定裕度,以防参数变化的影响。根据奈氏判据:对于最小相位系统,稳定的充要条件是开环幅相频率特性曲线TGH包围(-1,j0)点的圈数为0。当开环幅相频率特性曲线TGH穿过(-1,j0)点,闭环系统临界稳定。因此,在稳定研究中称(-1,j0)点为临界点,而闭合曲线TGH相对于临界点的位置即偏离临界点的程度,反应系统的相对稳定性。频域的相对稳定性即稳定裕度常用相角裕度 γ 和幅值裕度 h 来度量[1,2]。
本文的例题可以说明,笔者用于估算相位精度和幅值精度方法简便,且有较好的精度。经过大量系统验证了该方法是可行的,并在工程分析与设计中也能获得满意的结果。
1 系统的开环频率特性
设系统的开环传递函数为

式中,s是复变量;K为开环增益;τi和Tj为时间常数;v为开环系统s平面坐标原点上的极点的重数。
把式(1)中的s用jω代替就得系统开环特性:

2 相角裕度γ
2.1 直接利用定义求解
设ωc为系统的截止频率,有

由式(5)可解出 ωc,代入式(4)可求得 φ(ωc),代入式(6)求得相角裕度γ。但是由于要解反三角函数方程,因此当系统阶次较高时ωc很难求出,这正是此方法的局限所在。在工程设计和分析时,只要求粗略估计系统的相角裕度,我们一般先根据对数幅频特性渐近曲线确定截止频率ωc,即取ωc满足L(ωc)=0,再由相频特性确定相角裕度γ。
2.2 估算求法
幅频特性渐近曲线对系统在ωc处幅频值有影响的环节包括比例环节、积分环节、惯性环节、一阶微分环节和振荡环节等。近似计算在ωc处的系统幅值仅包括这些环节,且略去各环节的常数项1,这就是估算求法。
[例1]:求系统的开环传递函数为G(s)H(s)=5/s(s+1)(0.1s+1)的相角裕度和幅值裕度。
解:其开环频率特性为
G(jω)H(jω)=5/jω(jω +1)(0.1jω +1)
幅频特性为

相频特性为

转折频率为ω1=1和ω2=10。在0≤ω<1时,有 A(ω)≈5/ω。要使 A(ω)=1,则有 ω =5,这会与0≤ω<1矛盾,因此ωc不会在0到1之间;而在1≤ω <10 时,有A(ω)≈5/ω2,要使A(ω)=1,则有 ω =,在1≤ω <10区间,显然截止频率;在 ω≥10 时,A(ω)≈5/(0.1ω2),要使 A(ω)=1,则有 ω<10,与 ω≥10矛盾。故截止频率代入式(9)得γ=12o,可见它与实际γ=13.6o值很接近。
从例1可知估算求法只涉及到代数方程的求解问题,因此当系统阶次较高时要明显优于直接利用定义的方法。
3 幅值裕度h
设ωg为系统的穿越频率,则系统在ωg处的相角为 φ(ωg)=-180o,定义幅值裕度 h=1/A(ωg),幅值裕度的h含义是对于闭环稳定系统,如果系统开环幅频特性再增大h倍,则系统将处于临界稳定状态。故可根据劳斯判据来确定开环增益临界稳定K,从而求出h。由式(3)和式(4)可知变化开环增益K,相频特性不变,但幅频特性不同。所以ωg与开环增益无关,即不管K是多少,ωg是不变的。故可以在临界稳定时用上述估算求法求出ωg。
设上例中开环增益K1时系统临界稳定,开环传递函数:

我们由劳斯判据得系统临界稳定的充要条件是:1.1=0.1K1,所以系统临界稳定时 K1=11,所以据K1=5×h,求出幅值裕度h=22。对于下面两式应有相同的穿越频率ωg:

要使幅频特性满足
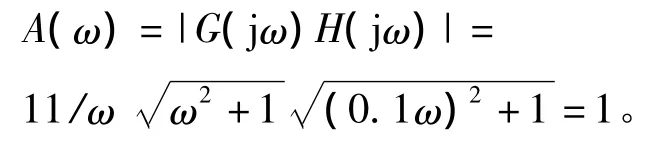
于是,在0≤ω<1时,有A(ω)≈11/ω。如果要使A(ω)=1,则得 ω =11,与0≤ω <1矛盾,故 ωg不会在0 到1 之间;在1≤ω <10,A(ω)≈11/ω2,如果要使A(ω)=1,则得 ω =3.31,在1≤ω <10 区间,故 ωg=3.31。将其代入式(9)后可得 φ(ω)≈181.4o,与定义φ(ωg)=180o很接近,证明其符合工程计算要求。
[1]胡寿松.自动控制原理[M].北京:国防工业出版社,1994
[2]绪方胜彦著.卢伯英等译.现代控制工程(中译本)[M].北京:科学出版社,1978.
