信号与系统中抽样定理的教学探讨

杨巧宁，李学斌，王学伟

(北京化工大学信息科学与技术学院，北京 100029)

抽样定理是“信号与系统”课程中重要的知识点，在连续时间信号的频域分析中讲解，国内外教材中均对其详细论述[1-4]。但是对初学学生来说，这个知识点的理解不够透彻，难以获得正确应用。为了要让学生深刻理解抽样定理，本文以时域抽样定理为例讨论教学过程的设计。

1 抽样和抽样定理

“抽样”就是利用周期抽样脉冲p(t)从连续信号f(t)中抽取离散样值的过程，得到的离散信号为抽样信号，也称为采样信号，以fs(t)表示。抽样过程的数学模型就是连续信号与抽样脉冲序列相乘。图1是连续信号时域抽样和从抽样信号恢复原连续信号的框图。

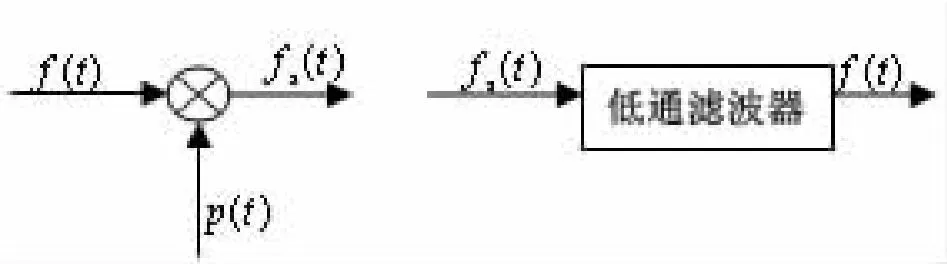
图1 连续信号时域抽样和连续信号恢复框图

连续信号时域抽样后，其频谱Fs(ω)是连续信号频谱F(ω)以抽样频率ωs为间隔周期重复的结果，幅度受到抽样脉冲p(t)的傅里叶级数系数Pn的加权[5]。

抽样定理的内容是:对于带限信号，其频谱占据－ωm～+ωm的范围，若信号可用抽样值来唯一地表示，则必须满足ωs≥2ωm或者Ts≤1/2fm

如果抽样频率满足抽样定理，则抽样信号通过截止频率为ωc(ωm＜ωc＜ωs－ωm)的低通滤波器，可由抽样信号fs(t)无失真复原信号f(t)。本文以理想低通滤波器恢复为例。

2 课堂教学方法

2.1 问题法

课堂教学中把内容问题化，以问题串起本节内容，可以帮助学生循序渐进理解知识点。整节内容提炼为五个问题，它们相互承接，概况了全部内容。

(1)为什么抽样?

这个问题让学生认识抽样的重要性和必要性，认识抽样的目的和意义。

数字信号处理技术的优势和快速发展使得数字设备和数字媒体广泛应用，如手机、MP3、CD和DVD等。抽样是连续信号变成数字信号非常关键的一步。在讲解抽样的过程和抽样的数学模型后，以第二个问题引出下一个重要知识点。

(2)抽样信号时域发生什么变化(抽样信号与连续信号的关系)?频域发生什么变化(抽样信号频谱和连续信号频谱的关系)?

这个问题可帮助学生理解抽样带来信号的实质变化。结合图形演示法讲解。详细过程见文献[5]。

抽样过程:

其物理意义是冲激抽样信号的傅立叶变换是连续信号频谱严格的周期重复。重复周期为抽样频率ωs，幅度受到常数1/Ts的加权，频谱形状不变。

(3)抽样信号是否保留连续信号的全部信息?

抽样信号在时频域变化讲解后，以问题启发学生进一步思考抽样的实质，第二问题和第三问题联系紧密，都为了说明抽样定理实质。

根据学生实时课堂的回答继续以问题启发，比如，抽样得到连续信号某些位置上的值，抽样信号是否应该反映连续信号的全部特征?为什么?要保留连续信号的全部信息和哪个指标有关?紧接着引出第四个问题，即引出重要知识点—抽样定理。

(4)抽样频率应该为多大?

这个问题帮助学生理解抽样定理研究的对象和实质，以及抽样定理的出发点。抽样必须保留连续信号的全部信息，抽样频率如何影响信息的保留度?实际抽样中，如何确定抽样频率?结合案例法和图形演示法讲解。在这里给出抽样定理的内容。

抽样定理理论给出后，可以再回到案例上进行重新分析，进一步加强对抽样定理的理解，可以结合实践法加深理解。

(5)如何从抽样信号不失真的恢复连续信号?

若满足抽样定理，抽样信号唯一的表示连续信号，则可由抽样信号不失真的恢复连续信号，如何恢复?结合图形演示法进行讲解。

如果能得到连续信号的完整频谱，则就得到了连续信号。满足抽样定理的条件下频谱不交叠，则可利用理想低通滤波器得到连续信号的完整频谱。理想低通滤波器的幅度和截止频率如何确定?理想低通滤波器(ωc－ωm≥ωc≥ωm):

2.2 案例法

理论分析讲解比较抽象，学生的理解不够透彻。如果对实际案例的应用采用直观形象的方法说明，初学学生对案例引入的知识点理解有帮助很大。

我们可以在提出第3、4和5个问题提出的时候，利用学生常见的实际信号:歌曲(语音信号)和照片(图像信号)，给出这两种实际信号不同抽样率下的结果。

图2所示是不同抽样率下图像的效果，包含图像失真严重、不失真及处于两者之间的图像效果。这些图像让学生直观看到抽样率的大小对信号的影响，对信号的保留或失真程度。明白抽样频率不够大时，重现信号会失真，如图2(a)和图2(b)所示。频率越大信号更接近原始信号，当大到一定值时，重现信号的信息已保留很好，再大时信号差异不明显，就会带来冗余，如图2(c)和图2(d)。学生便会提出:抽样频率应满足什么条件，应依据什么来选择?

图2 不同抽样率的图像

我们给出一段学生熟悉的音乐，采用不断降低抽样频率来收听音乐效果。让学生从听觉效果上分析抽样率对信号的影响，如图3所示。这里选择抽样频率时应包含:图3(a)为满足采样定理的语音;图3(b)为不满足采样定理的频谱交叠的语音;如图3(c)为不满足采样定理的抽样频率，且过小原始语音丢掉很多的语音，基本上听不出是什么旋律。

图3 不同抽样率对语音的影响

2.3 实践法

我们利用Matlab实现抽样定理的程序，对图像和语音这非典型一维信号进行抽样。课堂上现场演示，让学生任意给定抽样频率。给出满足、不满足和临界满足采样定理的情况，如图4所示。

图4 信号抽样例子

上图中给出了其中一个处理结果。左边一列是不同抽样率下的原始时域信号，右边一列是对应的频谱。这种方法给学生展示了实时可变的动态图形。让其了解抽样信号的变化、频谱的变化、抽样率对信号的影响、不同抽样率的信号恢复效果及与原信号之间的关系。

2.4 图形演示法

在问题法(2)的理论讲解完后，以图形的形式演示抽样过程，如图5所示。学生可以直观看到怎样抽样、抽样信号和原信号的关系、抽样后频域的变化及抽样信号频谱与原信号频谱的关系。

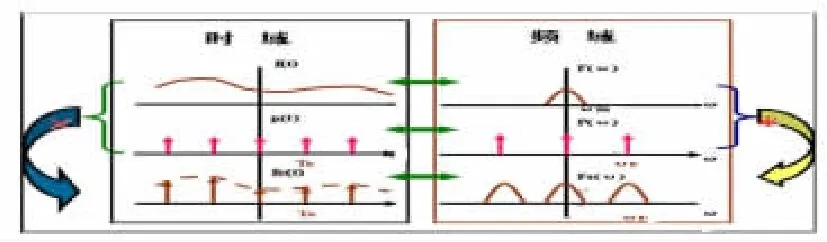
图5 抽样过程及频谱变化

在问题法(4)的抽样定理内容讲解之前，通过图形演示分析。要得到原信号完整频谱，抽样频率应满足的条件，从而引出抽样定理内容。在问题法(5)之前可借助满足采样定理的图形演示，分析恢复原始信号的方法原理如图6所示。

图6 恢复信号的方法原理

3 结语

本文通过问题法、案例法和实践法图形演示法讲解抽样定理，帮助学生掌握和深刻理解抽样定理的内容。问题法有利于启发思维，激励创新，图形演示法有利于得到直观认识，案例法有利于理解实际应用，实践法有利于倡导活学活用。我们将这些方法有机结合来讲述抽样定理，对教科书内容给予很好的补充，取得了很好的教学效果。

[1]奥本海姆著，刘树棠译.信号与系统(第二版)[M].西安:西安交通大学出版社，1998

[2]管致中，夏恭恪，孟桥.信号与线性系统(第四版)[M].北京:高等教育出版社，2004

[3]吴大正，信号与线性系统分析(第四版)[M].北京:高等教育出版社，2006

[4]陈后金，胡健等.信号与系统[M].北京:高等教育出版社，2003

[5]郑君里，应启珩，杨为理.信号与系统[M].北京:高等教育出版社，2000