三、四点角接触球轴承游隙计算的分析

孙慧广，寇思源

（1.中国人民解放军驻哈尔滨轴承集团公司军事代表室，黑龙江 哈尔滨 150036；2.中航工业哈尔滨轴承有限公司 研发中心，黑龙江 哈尔滨 150036）

文中涉及到的符号及其含义：

α—接触角，

Pd—径向测量游隙，

Pe—轴向测量游隙，

ri—内圈沟曲率半径，

re—外圈沟曲率半径，

Dw—钢球直径，

as—三点接触时的垫片角，

βs—四点接触时的垫片角，

Xi—内圈沟曲率半径中心横坐标，

Xe—外圈沟曲率半径中心横坐标。

1 前言

三、四点角接触球轴承广泛的应用于同时承受轴向、径向力的场合，在航空、航海机械中大量使用。在实际使用中该类轴承的游隙与普通的角接触轴承的计算、测量有较大的差异，本文试就三点和四点轴承的计算、测量进行简单的分析，试给出合理的几何关系。

在普通的角接触球轴承中，接触角与轴承游隙的几何关系较为简单：

而在三点角接触球轴承中，由于沟道半径中心的偏移，其几何关系也随之进行了变化，此时需要将三点角接触球轴承中的几何关系先还原为普通角接触形，然后再按照普通角接触形进行计算。

2 三、四点角接触球轴承结构

2.1 三点角接触球轴承（图1）

2.1.1 双半外圈角接触球轴承

双半外圈的角接触球轴承，内圈与同规格尺寸的外圈斜坡角接触球轴承内圈一致，而外圈则是进行了沟心位置的横向位移。

2.1.2 双半内圈角接触球轴承

双半内圈的角接触球轴承外圈与同规格尺寸的内圈斜坡角接触球轴承外圈一致，而内圈则是进行了沟心位置的横向位移。

2.2 四点角接触球轴承

四点角接触球轴承一般外圈为整体，而内圈为双半。外圈为整体，沟道为两部分，有时带退刀槽，有时不带；内圈为双半内。其结构形式如下图 2 所示。

图1 三点角接触球轴承

图2 四点角接触球轴承

3 轴承内部几何关系

3.1 双半外圈三点角接触球轴承

3.1.1 径向游隙与接触角

3.1.2 轴向游隙与接触角：

3.1.3 径向游隙与轴向游隙

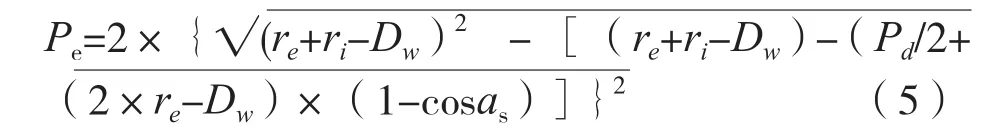
3.2 双半内圈三点角接触球轴承

3.2.1 径向游隙与接触角

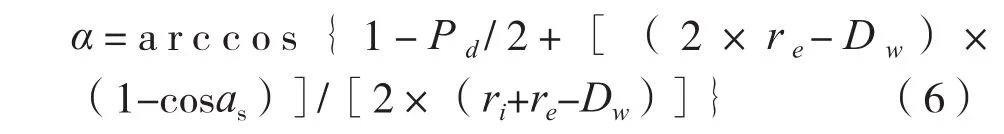
3.2.2 轴向游隙与接触角

3.2.3 径向游隙与轴向游隙

3. 3 四点角接触球轴承

四点角接触球轴承的几何关系较为复杂，需要考虑内、外圈沟心位置变化对游隙造成的影响。

3. 3.1 径向游隙与接触角

化简后得：

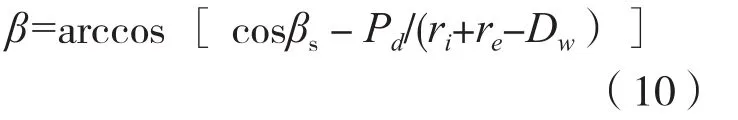
3.3.2 轴向游隙与接触角

3. 3.3 径向游隙与轴向游隙

4 对比分析

4.1 三点接触

某型双半内圈角接触球轴承参数：钢球直径22.225 mm，外沟曲率半径11.mm，内沟曲率半径11mm，垫片角25°，内圈沟曲率半径中心横坐标mm，径向游隙0.229mm～0.274mm。

（1）按以往的公式计算得：接触角3 3.2°～4 1.5°，轴向游隙为：0.537mm～0.698mm。

（2） 按改进的公式计算得：接触角3 4.6°～4 0.0°，轴向游隙为：0.602mm～0.848mm。

4.2 四点接触

某型双半内圈角接触球轴承参数：钢球直径24.606mm，外沟半径mm，内沟半径mm，垫片角26°，内圈沟曲率半径中心横坐标mm，外圈沟曲率半径中心横坐标径向游隙0.15mm～0.18mm。

（1）按以往的公式计算得：接触角25.3°～34.1°，轴向游隙为：0.182mm～0.457mm。

（2）按改进的公式计算得：接触角30.8°～34.3°，轴向游隙为：0.769mm～1.520mm。

由以上的计算结果可以看出，改进前后的接触角及游隙转化都有较大的出入，主要是由于以往的计算公式没有考虑偏沟位移带来的游隙的改变。

5 结束语

三、四点角接触球轴承，就是普通角接触球轴承的特殊形式。有其基本的共同原理。三、四点角接触球轴承的测量游隙与普通角接触球轴承的测量游隙不同，普通的角接触的测量游隙就是它的计算游隙，三、四点角接触球轴承的测量游隙不是它的计算游隙，计算游隙需要进行计算。改进后的接触角与游隙转化公式更符合轴承内部几何关系，较以往的计算公式更合理的指导生产服务。

［1］王献锋，等.三点四点接触球轴承接触角和游隙的计算[J].轴承, 2006,(6).