码率自适应原模图LDPC码的设计

王志娜，肖 旻，王 琳

（1.重庆邮电大学重庆市移动通信重点实验室，重庆 400065;2.厦门理工学院电子工程系，福建厦门 361005;3.厦门大学通信工程系，福建厦门 361005）

0 引言

通信系统业务的多样性、信道的时变性、物理层技术的灵活性需要信道编码码率能够自适应地根据信道环境做出相应的调整。采用码率自适应的编码技术，可以在保证系统服务质量的前提下，根据信道的状况及时调整码率，从而提高通信系统的频谱利用率。

低密度奇偶校验码［1］（low density parity check code，LDPC）具有良好的距离特性、小的误码率和较低的译码复杂度，被认为是迄今为止纠错性能最好的码。2003年，美国国家航空航天局的空气动力实验室（JPL）首次提出了原模图 LDPC码［2］（protograph LDPC codes），弥补了传统LDPC码编码复杂度较高的不足。作为一种原模图LDPC码，AR4JA码［3］（accumulate repeat－4 jagged－accumulate code）最大的优势就是错误地板极低。该码的性能优于绝大多数的一般LDPC码和其他原模图LDPC码，2006年由太空数据系统咨询委员会（consultative committee for space date systems，CCSDS）推荐给 NASA 作为深空通信的标准码型。鉴于原模图LDPC码，尤其是AR4JA码的各种优势，对原模图LDPC码率自适应的研究有着很广阔的前景。

目前，实现码率自适应的方法主要有删余和扩展两种。删余可以利用同一对编译码器对不同码率的码进行编译码，是最常用的一种码率自适应方法。2006年，J.Ha等［4］借鉴“恢复”的概念，定义了删余变量节点（punctured variable node，PVN）的“恢复级别”。PVN的恢复级别是影响删余码型性能的重要因素，之后，对删余算法的研究实质上都是基于PVN 的恢复级别进行的［5－8］。然而，J.Li等［9］表明，随着删余码率的增加，码的性能离香农限的距离增大，仅仅依靠删余并不能在较大码率范围内得到好性能的码。为了得到更大范围变化的码率，通常将删余和扩展结合起来构造码率自适应码组。

现阶段，对一般LDPC码率自适应的研究已经取得了很多成果。然而，对原模图LDPC码率自适应的研究却较少。目前，只有 El－khamy等［10］以一个低码率的原模图LDPC码（accumulate repeat check accumulate code，ARCA 码）为基础，利用删余的方法实现码率自适应，得到的码率自适应ARCA码有较高的错误地板。与之不同的是，本文将拥有极低错误地板的AR4JA码作为母码，通过删余和扩展相结合的方法来构造码率自适应AR4JA码（ratecompatible AR4JA，RC－AR4JA）。

1 原模图LDPC码

1.1 原模图LDPC码基本原理

原模图是一种包含相对较少节点的Tanner图。一个原模图Gp=（V，C，E）包含变量节点集V，校验节点集C和边集E。每一条边e=（V，C）∈E连接一个变量节点v∈V和一个校验节点c∈C。原模图中允许有平行边的存在，因此e→（vi，cj）∈E并不是一一映射关系。与原模图对应的校验矩阵称为基础矩阵B，Bij的值代表第i个校验节点和第j个变量节点之间连接边的条数。与一般LDPC码校验矩阵不同的是，Bij的值并不仅限于0和1。对原模图进行T次复制，然后把T条相同类型的变量节点和校验节点之间的边置换，可以扩展成不同大小的图。我们称这种图为导出图G，对应的LDPC码称为原模图LDPC码。

作为一个简单的例子，我们考虑如图1所示的原模图，其中圆圈代表变量节点，方框代表校验节点。图1a的原模图Gp有个变量节点，个校验节点，条边。图1b是将图1a的原模图Gp复制T=2次得到的大图，这2个相同的子图之间是相互独立，互不相连的。将图1b中相同类型节点之间的边进行置换，便得到图1c所示的导出图G，此时这2个子图就连接在一起了。

图1 原模图到导出图的过程Fig.1 Process from protograph to derived graph

原模图中，允许变量节点集V包含删余变量节点。假设有Vu个删余变量节点，则未删余变量节点个。那么码率的计算将变为R=

1.2 AR4JA码

AR4JA码是一种特殊的累加重复累加码［11］（accumulate repeataccumulate codes，ARA）。码率为1/2的AR4JA的编码框图，原模图如图2所示，其中I表示交织器，D表示累加器，空心圆圈代表删余变量节点，实心圆圈代表未删余变量节点，方框代表校验节点。该码的原模图有个变量节点，个校验节点，其中有1个变量节点被删余了。（1）式为该码的基础矩阵。AR4JA码是一种系统码，即:变量节点3和4代表信息位，变量节点0，1和2代表校验位。码率为1/2的AR4JA的迭代译码门限为 0.628 dB，典型最小距离比为 δmin=0.015［3］。

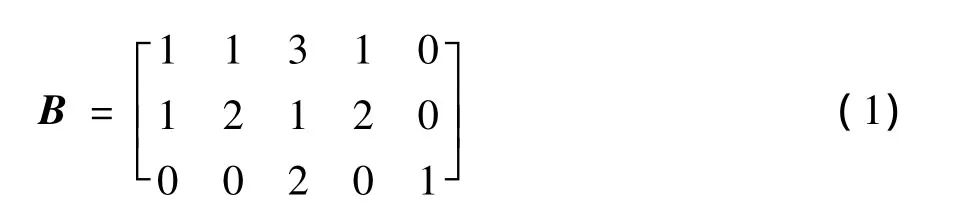
图2 码率为1/2的AR4JA码Fig.2 AR4JA code of rate 1/2

AR4JA码具有传统LDPC码的优点，作为一种ARA码，还可以通过简单的重复器和累加器进行编码，编码简单快速更易于硬件实现。此外，它的最小距离以很高的概率与码长成线性关系［12－13］，克服了一般原模图LDPC码错误地板欠佳的不足。

2 RC-AR4JA码的设计

对于RC－AR4JA码的设计，我们选取码率为1/2的AR4JA码作为母码，并分两部份进行。首先，提出“逐节点删余”算法实现码率由0.5～0.8的自适应。其次，利用矩阵扩展的方法获得码率从0.5～0.25的RC－AR4JA码。结合删余和扩展的方法，能够实现码率在0.25～0.8变化的 RC－AR4JA 码。

2.1 “逐节点删余”算法

删余的基本思想:首先选取一个较低码率及性能优良的码作为母码，通过删余母码的冗余变量节点得到一系列高码率的码。

2.1.1 基本准则

在进行删余时，我们提出以下准则，依据这些准则依次删余满足条件的变量节点，直到获得想要的高码率。

准则1 最大化最低恢复级别PVN个数。

准则2 最小化删余变量节点通过校验节点相连的所有PVN数目。

准则3 最小化每个校验节点上连接PVN个数。

2.1.2 算法主要步骤

“逐节点删余”算法的具体步骤表述如下（参数见表1）。

表1 “逐节点删余”算法的参数Tab.1 Parameters of the“puncturing node by node”algorithm

步骤1 通过（2）式计算要删余的节点数目

步骤2 找到集合U，并对于每一个c∈N（v），其中v∈U，计算出被删余 。

步骤3 对于每一个v∈U，通过（3）式计算出G（v），H（v）和M（v）。

步骤4 找到集合T={vr:vr∈U＆G（vr）=minv∈U G（v）}，如果T中只有一个节点，删余该节点，并跳到步骤5。

步骤4.1 找到集合W={vr:vr∈U＆H（vr）=minv∈T H（v）}，如果W中只有一个节点，删余该节点，并跳到步骤5。

步骤4.2 找到集合D={vr:vr∈U＆M（vr）=minv∈W M（v）}，如果D中只有一个节点，删余该节点。如果D中有多个节点，随机选取一个进行删余。

步骤5 判断删余的变量节点数目是否等于Npun，若是，则结束;否则，跳到步骤2。

2.2 矩阵扩展

扩展是选取一个较高码率及性能优秀的码作为母码，通过增加额外的冗余比特来降低码率。扩展有两种方法:矩阵扩展和校验节点分裂。矩阵扩展是最早提出的一种扩展方法［9］，如图3所示。首先选取一个较高码率母码的校验矩阵，为N0列M0行。当码率需要降低的时候，依次增加Mi行和Mi列，从而得到一系列码率为Ri＜R0的码，其中Ri=为了保证母码的特性，扩展后的矩阵右上角全为0，同时左下角的“稀疏矩阵”也需要保证与原矩阵之间的非相关性。对于扩展矩阵中的Bi，不同的码具有不同的构造方式。

图3 矩阵扩展Fig.3 Matrix expansion

对于AR4JA码，采用如图4所示的扩展方法，左上角3T×5T的矩阵为母码的校验矩阵。在左下角的“稀疏矩阵”设计时，本文保证新增校验节点的度为4，并且使得新增的校验节点只与母码中2号和3号变量节点相连。右上角的0代表全零矩阵，右下角的1代表单位矩阵，这样便可以得到码率为R=T/（2T+M）的AR4JA码。

图4 AR4JA的矩阵扩展Fig.4 Matrix expansion of AR4JA code

新增校验节点的度为4，使得扩展后的矩阵校验节点度更加集中，有利于码的性能［14］。为了进一步提高性能，采用改进的PEG算法对新增校验节点与变量节点的连接进行优化，避免了Tanner中短环的出现。

3 仿真结果及分析

我们用上述方法构造RC－AR4JA码，并进行了仿真。其中，母码采用扩展次数为512的 AR4JA码，即信息位长度为1 024，码率为1/2，其中在扩展时采用改进型的PEG算法［15］来消除6环。仿真在AWGN信道下进行，采用 BPSK调制，Log－BP译码算法，最大迭代次数为100。

首先，采用“逐节点删余”算法设计RC－AR4JA码，实现了码率从0.5～0.8的变化，并与随机删余构造的RC－AR4JA码进行了对比。图5给出了这两种RC－AR4JA码的性能仿真曲线。为了使不同码率的仿真结果更加清晰，本文给出了Es/N0与BER的曲线，其中Es/N0=Eb/N0+10lgR。

相对于随机删余，采用“逐节点删余”设计的RC－AR4JA码具有更好的性能，随着速率的增加优势进一步扩大。在BER为10－6数量级（无线数据通信业务的标准 BER），逐节点删余设计的 RCAR4JA码在码率分别为0.6，0.7的情况下，比随机删余获得的 RC－AR4JA 码分别有约 0.5 dB，1.0 dB的增益。在码率为0.8时，随机删余与逐节点删余的差距更大。

图5 不同删余算法下的RC－AR4JA码性能Fig.5 BER performances of RC－AR4JA codes with different algorithms

其次，采用图4所示矩阵扩展的方法，设计了码率从0.5～0.25的 RC－AR4JA 码。作为对比，还利用随机扩展构造0.5～0.25码率变化的AR4JA码。在随机扩展时，保证新增校验节点度同样为4，两者之间的对比将是公平的。图6给出这两种扩展方法得到的RC－AR4JA码的性能仿真曲线。图6中，选择表示本文设计的扩展方法，随机为随机扩展方法。

图6 不同扩展方法得到的AR4JA码性能Fig.6 BER performances of RC－AR4JA codes obtained by differentmatrix expansion method.

相同的码率下，用图4所示矩阵扩展构造的RC－AR4JA码较随机扩展有更好的性能，随着码率的降低，这种优势更加明显。在BER为10－6数量级，用本文的扩展方法构造的AR4JA码在码率分别为 0.4，0.35，0.3 和 0.25 的情况下，较随机扩展得到的 AR4JA 码分别有 0.2 dB，0.5 dB，0.7 dB 和 1 dB的增益。此外，我们设计的 RC－AR4JA码，在BER为10－6数量级并未出现错误地板。

4 结束语

本文针对一类拥有极低错误地板的原模图LDPC码—AR4JA码，提出了“逐节点删余”算法，实现了码率由0.5～0.8的增加，并利用矩阵扩展的方法构造了码率从0.5～0.25变化的AR4JA码。结合删余和扩展的方法，实现码率从0.25～0.8灵活变化的RC－AR4JA码。在AWGN信道下的仿真结果表明，在 BER为10－6数量级处，本文设计的 RCAR4JA码在整个码率变化范围内并未出现错误地板，保持了母码错误地板低的优良特性。

［1］GALLAGER R G.Low－density parity check codes［M］.Cambridge，MA:MIT Press，1963.

［2］THORPE J.Low－density parity－check（LDPC）codes constructed from protographs［C］//Tech.Rep.Progress Report.Pasadena，CA，USA:JPL IPN，2003:42－154.

［3］ DIVSALAR D，JONESC，THORPE J.Protograph based LDPC codeswithminimum distance linearly growing with block size［C］//IEEE.IEEE Communications Society subject.ST，louis:IEEE Globecom，2005:1152－1156.

［4］HA J，KIM J，KLINC D，et al.Rate－compatible punctured low－density parity－check codes with short block length［J］.IEEE Trans Inform Theroy，2006，52（2）:728－738.

［5］胡文江，卫霞.码率自适应 QC－LDPC码的研究［J］.重庆邮电大学学报:自然科学版，2009，21（1）:53－56.

HUWen－jiang，WEIXia.Design of rate－compatible QCLDPC codes［J］.Journalof Chongqing University of Posts and Telecommunications:Nature Science Edition，2009，21（1）:53－56.

［6］ YOU Ying，XIAOMin，WANG Lin.The rate－compatible Multi－Edge Type LDPC codes with short block length［C］//IEEE.Proceedings of the 5th International Conference on Wireless communications（WiCOM'09）.NJ，USA:IEEE Press，2009:1－4.

［7］肖旻，黎勇，王琳.码率自适应LDPC码删余算法［J］.应用科学学报，2011，24（9）:385－389.

XIAOMin，LIYong，WANG Lin.Puncturing Algorithm for design rate－compatible LDPC codes［J］.Journal of applied sciences，2011，24（9）:385－389.

［8］ 温娜，徐永太，张平.有限长LDPC码的打孔方案设计［J］.北京邮电大学学报，2007，29（6）:135－138.

WEN Na，XU Yong－tai，ZHANG Ping.Design of puncturing scheme for finite－length LDPC codes［J］.Jouranl of Beijing University of Posts and Telecommunications，2007，29（6）:135－138.

［9］LI J，NARAYANNA K.Rate－compatible low density parity check codes for capacity－approaching ARQ scheme in packet data communications［C］//Proc.Int Conf Comm Internet and Info.Tech（CIIT）.Virgin Islands，USA:2002:201－206.

［10］ MOSTAFA E1－Khamy，HOU Ji－lei，BHUSHAN Naga.Design of rate－compatible structured LDPC codes for Hybrid ARQ application［J］.IEEE JSele Areas Commun，2009，27（6）:965－973.

［11］ ABBASFAR A，DIVSALAR D，YAO Kung.Accumulate repeat accumulate codes［C］//IEEE International Symposium on Information Theory（ISIT）.Chicago，USA:IEEE Globecom，2004:509－513.

［12］ DIVSALAR D.Ensemble weight enumerators for protograph LDPC codes［C］//IEEE.IEEE International Symposium on Information Theory（ISIT）.Seattle，Washington，USA:IEEE Press，2006:1554－1558.

［13］ DIVSALAR D，DOLINAR S，JONSC R，et al.Capacity－approaching protograph codes［J］.IEEE J sele Areas Commun，2009，27（6）:876－888.

［14］ CHUNG SY，RICHARDSON T J，URBANKE R L.A－nalysis of sumproduct decoding of low－density paritycheck codes using a Gaussion approximation［J］.IEEE Trans Inform Theory，2001，47（2）:567－570.

［15］ BONELLO N，CHEN Sheng，HANZO L.Construction of regular Quasi－Cyclic protograph LDPC codes based on vandermondematrices［J］.IEEE Transactions Veh Technol，2008，54（4）:2583－2588.