搭线窃听下网络安全路径及安全网络编码的研究

朱联祥，朱艳艳，曹 铮

（重庆邮电大学信号与信息处理重庆市重点实验室，重庆 400065）

0 引言

网络编码的出现，带来了不可忽视的安全问题。按照攻击者对网络安全的攻击方式分，主要包括污染和窃听两类，其中污染为主动攻击，搭线窃听为被动攻击。由于被动攻击不对消息做任何修改，因而是难以检测到的，已有不少学者对窃听攻击做了大量的研究。

Cai和Yeung［1］提出了一种基于安全网络编码的网络窃听模型，并给出一个利用网络编码实现网络安全的充分条件。K.Jain［2］在Cai和Yeung提出的窃听模型的基础上，证明了只要存在一条从源节点到宿节点的路径不被窃听，网络就是安全的。Bhattad和Narayanan［3］首次分析了一种弱安全模型，当窃听者窃听到的信道数小于网络的最大流时，设计了一种弱安全的网络编码。Lima等［4］则考虑了窃听者窃听节点而不是信道这样一种更一般的情形。

目前网络编码最主要的2种实现方式是线性网络编码［5］和随机网络编码。从线性网络编码代数构造角度构造的安全网络编码是一种确定性编码方案，在进行网络编码时需要知道网络的拓扑结构。随机网络编码是一种分布式的编码方案，设计者不需知道整个网络的拓扑结构就可以进行编码。本文是基于给定的网络拓扑图进行的研究，将采用线性网络编码代数构造方法。

1 窃听攻击下网络的安全路径

1.1 思想背景

搭线窃听，是指攻击者以窃听为手段获取网络中信源到信宿某些路径上传送的信息。网络被窃听时，安全的网络编码是必要的。通常，设计者假设窃听者知道通信双方的编码方案，并能根据自己的知识尽可能地选取窃听路径。一般地，将这个窃听动作看成是攻击者能够获取一个边集合的某个子集中的所有边上的信息，当这个子集中的元素最多有P个时，窃听者每次最多能获取P条边上的信息。窃听者一次只能窃听到窃听类集A={A1，A2，…，An}中的一个子集Ai，其中Ai⊂A，而设计者只知道窃听类集A，却不知道究竟其中的哪个子集被窃听。

因此，第一种情况，当网络的全部路径被窃听时，该网络一定不安全，这是最严重的情况;第二种情况，当一个给定的通信网络遭到窃听攻击时，若找不到一条安全的从源到宿（多播网络时为多个宿）的路径，则该网络仍然是不安全。由此可见，在设计编码方案前，首先要判断网络是否有安全路径存在。

Kamal Jain［2］在文献中针对单源单宿网络提出了一个安全定理，该定理假定窃听者仅具有有限的计算能力。

令S⊂V是节点的集合，且s∈S，t∉S，δ0（S）表示集合S到集合）的截边集，即表示集合到 集 合S的 截 边 集，即

定理1 对于一个窃听集Ai∈Α，如果对于任意的集合S（s∈S，t∉S），有δ（S）⊄Ai，即至少存在一条边e∈δ（S），但e∉Ai，则窃听者获得不了关于信源的任何有用信息。

这个定理的本质是要求源和宿之间至少有一条安全路径，从而通过拓展这条安全路径来构造安全网络编码。

文献［7］结合上述的安全定理，不考虑修剪过后网络图的方向性，介绍了一种基于广度优先算法（breadth first search，BFS）的寻找单源单宿网络中安全路径的算法。该算法仅适用于寻找单源单宿网络的安全路径，并不适用于单源多宿网络，有一定的局限性［7］。

本文中我们通过考虑网络拓扑图的有向性，并利用有向图生成树算法的思想，提出了一种新的算法。新的算法不仅可将窃听网络图中从源节点到宿节点的所有安全路径找出，而且算法适用于单源单宿网络和单源多宿网络。对于单源多宿网络，只要有一个宿节点和源节点间不存在一条不被窃听的安全路径，网络没有达到多播的目的，该网络就不是安全的。

1.2 寻找单源单宿及多宿网络安全路径的算法

定义1 除源节点和宿节点之外的一组节点集，它们分别既有从源节点到该节点的路径又有从该节点到宿节点的路径，称这些节点和路径为网络拓扑图的相关部分。除此之外的，均称为不相关部分。

如图 1 所示，图 1a中节点a，b，c及边 （s，a），（b，t），（s，c），（t，c）均为网络不相关部分，其中a，b为悬挂节点，（s，a），（b，t）为悬挂边。修剪掉这些网络不相关部分，可得修剪后的网络拓扑图如图1b所示。

图1 网络的不相关部Fig.1 Not relevant parts of the network

由于网络不相关部分不传送任何信息，它们是否被窃听无关紧要，所以本文研究的网络拓扑图均为修剪过的网络图。对于给定的一个通信网络，删除掉网络不相关部分，把修剪过的网络仍用G=（V，E）表示。

令每条边上的权值

则单源单宿及多宿网络拓扑图中寻找从源到宿安全路径的算法可描述如下。

1）输入:修剪后的网络拓扑图的关联矩阵G，源节点s和宿节点t（单宿）或t1，…，tn（多宿），以及相应的权值矩阵F，并初始化最终安全路径拓扑图的邻接矩阵W为空阵。

2）检查源节点下游节点的安全性。若源节点所有邻接路径均被窃听，即权值F（（u，v））=0，则W为空阵，跳出程序;若源节点所有邻接路径不全被窃听，即邻接路径F（（u，v））不全为0，跳入3）。

3）检查除宿节点之外的所有节点下游邻接边的安全性，即权值 F（（u，v）），若 F（（u，v））=1，则 W（（u，v））=1 。

4）由3）中得到的邻接矩阵W可得新的网络拓扑图，去除此时图中的悬挂边。在由3）得到的邻接矩阵W的基础上，若某一W（（u，v））=1，v为u的邻接下游节点，不满足 W（s，…）=W（…，u）=W（（u，v））=W（v，…）=W（…，ti）=1（单宿时，i=1;多宿时，i∈1，…，n），则 W（s，…）=W（…，u）=W（（u，v））=W（v，…）=W（…，ti）=0 。跳出程序。

最后的邻接矩阵W只有2种情况:第1种情况，W为空阵，说明网络不是安全的;第2种情况，从W中可以得到所有的从源到宿的安全路径，W（s，…）=W（…，u）=W（（u，v））=W（v，…）=W（…，ti）=1（多宿时，i∈ 1，…，n）。

该算法也有一定的局限性。应用该算法的前提是要已知窃听子集，若只知道窃听类集而不知道具体的窃听子集，则无法应用该算法。

2 存在从源到宿安全路径的单源多宿网络

2.1 信息论安全与弱安全

抗搭线窃听的安全网络编码大体上分为2种，一种是信息论意义下的安全网络编码，一种是弱安全的安全网络编码。设X为源信息，M为窃听者窃听到的信息，若有I（X;M）=0，则窃听者没有得到关于X的任何信息，称为信息论意义的安全;若有I（X;M）≠0，I（xi;M）=0，其中xi∈X，则窃听者没有得到关于X的任何有意义的信息，称为弱安全。

弱安全的网络编码是由K Bhattad［3］提出的，例如，窃听者得到了关于源的2个比特的异或，他虽然得到了关于源的一个比特的信息，但却无法得到关于源的任何“有意义”的信息。在实际应用中这样的安全性就足够了，这样的安全性是弱于信息论安全的，故称之为“弱安全”。

当网络遇到窃听攻击时，在存在从源到宿安全路径的情况下要考虑的是此时网络还是否安全。对于单源单宿网络，只要找到一条通向宿节点不被窃听的路径，网络就是安全的。而对于单源多宿网络，即使存在一组到各宿节点不被窃听的路径时，网络也可能是不安全的，那么窃听者是不能得到有关源的任何信息即信息论意义上的安全，还是不能得到有关源的任何有意义的信息即弱安全，还是完全能够恢复出源消息。从而安全的网络编码方案起到关键性作用。设计者的任务是设计一个安全网络编码方案，使得网络在已被攻击者窃听的情况下，要么达到信息论意义下的安全，要么达到弱安全。

2.2 线性网络编码代数构造方法

本节先介绍线性网络编码代数构造方法的基本思想，然后以一通信实例说明单源多宿网络，即使存在一组到各宿节点不被窃听的路径时，网络也可能是不安全的［6，8］。

2.2.1 数学模型

源节点s上生成的μ（S）个离散随机过程X（s，l），1≤l≤μ（S）的集合用 X（S）={X（s，1），X（s，2），…，X（s，μ（S））}表示。ν（t）个随机过程 Z（t，l）的集合 Z（t）={Z（t，1），Z（t，2），…，Z（t，v（t））}表示宿节点的输出信息。当有n个宿节点时，输出信息 Z={Z（t1，1），…，Z（t1，ν（t1）），…，Z（tn，1），…，Z（tn，ν（tn））}。

令G=（V，E）表示无延迟线性通信网络，长度为m的任何二进制向量可以被认为是域F2m（包含2m个元素的有限域）中的元素，如果G的所有边上传输的随机过程Y（e），e=〈v，v'〉∈E满足条件

（2）式中编码系数 αe，l和 βe'，e是有限域F2m的元素，则称G是一个F2m线性网络。

任何宿节点t的输出 Z（t，l），l∈ {1，2，…，v（t）}都是由随机过程Y（e），e∈ΓI（t）构成，定义Z（t，l）是Y（e），e∈ΓI（t）的线性组合，即

（3）式中，编码系数 εe，j是F2m的元素。

F2m无延迟线性通信网络的最重要的结论是用系统转移矩阵来描述输入向量X和输出向量Z之间的关系。用M表示输入向量X和输出向量Z网络的系统转移矩阵Z=XM。

定义2 给定网络编码数学模型，即对于一个网络编码问题，如果存在编码系数 αe，l，βe'，e和 εe，j，并将这些编码系数 αe，l，βe'，e和 εe，j用系统转移矩阵M 表示，如果能够找到合适的编码系数 αe，l，βe'，e和εe，j使得转移矩阵M满秩，则这网络编码问题是可解的，即信源节点可以成功译码，且X=ZM－1，称一组编码系数 αe，l，βe'，e和 εe，j即为一个编码方案。

2.2.2 通信实例

如图 2所示，假设窃听类集为 {A1，A2}={{e4，e6，e7，e9}，{e6，e7，e10，e13}}。

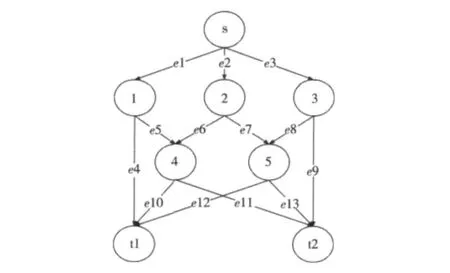
图2 单源多宿网络拓扑图Fig.2 Single soure and multi－ sink network

设计者只知道窃听类集，而不知道具体的窃听子集。无论是窃听子集A1还是A2，利用2.2节中的算法，可得最终的安全路径邻接矩阵为

可以找到从源到2个宿节点的不被窃听的全部安全路径。当窃听子集为A1时:s→1→4→t1（t2），s→3→5→t2（t1）;当窃听子集为A2时:s→3→5→t1，s→1→4→t2，s→1→t1，s→3→t2。

由网络最大流最小割定理可知，图2的最大传输容量为3。源节点s上的输入过程用向量X={X（s，1），X（s，2），X（s，3）}表示，宿节点t的输出过程用向量 Z={Z（t，1），Z（t，2），Z（t，3）}表示。

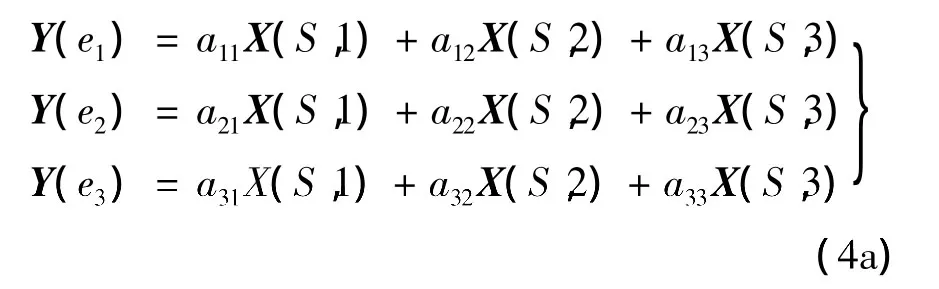
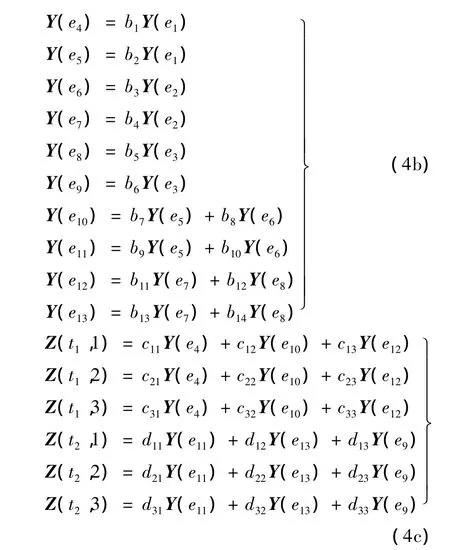
由Z=XM并结合（4）各式，我们可以得到

若要让宿而且是每一个宿都能准确恢复信源消息，那么在编码时，不仅矩阵M需满秩，而且分块矩阵ab1c，ab2d均需满秩，即a，b1，b2，c，d均要满秩。则b1=1，b6=1，且b3，b4不能为0。

窃听子集A1={e4，e6，e7，e9}的窃听矩阵为P1:

要使窃听者得不到关于信源的信息，即不能使窃听者还原出源消息，则P1和P2均不能满秩。前面已分析出a满秩，b1=1，b6=1，b3=1，b4=1，则P1必满秩;而在M满秩的情况下P2能够不满秩。说明当窃听者窃听到边集A1={e4，e6，e7，e9}时，可以还原源消息，网络一定是不安全的;当窃听到边集A2={e6，e7，e10，e13}时，网络的安全性是弱安全。

通过以上分析，可以得到这样一个结论，当存在一组数使窃听矩阵不满秩而系统转移满秩，则网络是安全的;当不存在一组数使窃听矩阵不满秩而系统转移满秩，则网络是不安全的。线性网络编码的代数构造方法，不需要知道确切的窃听子集，并且给定了在检验到网络安全时宿节点恢复出源消息的方法。

2.3 一种改进的线性网络编码代数构造方法

对线性网络编码代数构造方法的运用，是以窃听者知道设计者的编码方案为前提的。在这种情况下，如果窃听者窃听到了网络的全部路径，或网络中不存在从源到宿的安全路径，网络一定是不安全的。若使信源产生的信息为X'，X'为X的某种变换，窃听者不知道这种变换方式，而其他节点的编码方式仍用线性网络编码的代数构造方法，则即使窃听者窃听到全部的网络路径，根据第2.1节提到的弱安全性，I（X;M）=I（X;X'）≠0，而I（xi;X'）=0，达到了网络弱安全。

改进的源节点对源信息的变换方法。

1）选取一对角矩阵

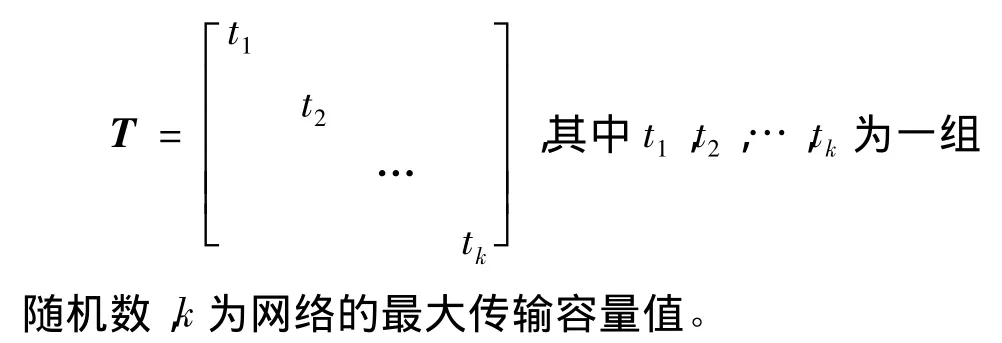
2）源信息X左乘T。

3）对2）中得到的结果每个信息包中加入一个单位的冗余，得到

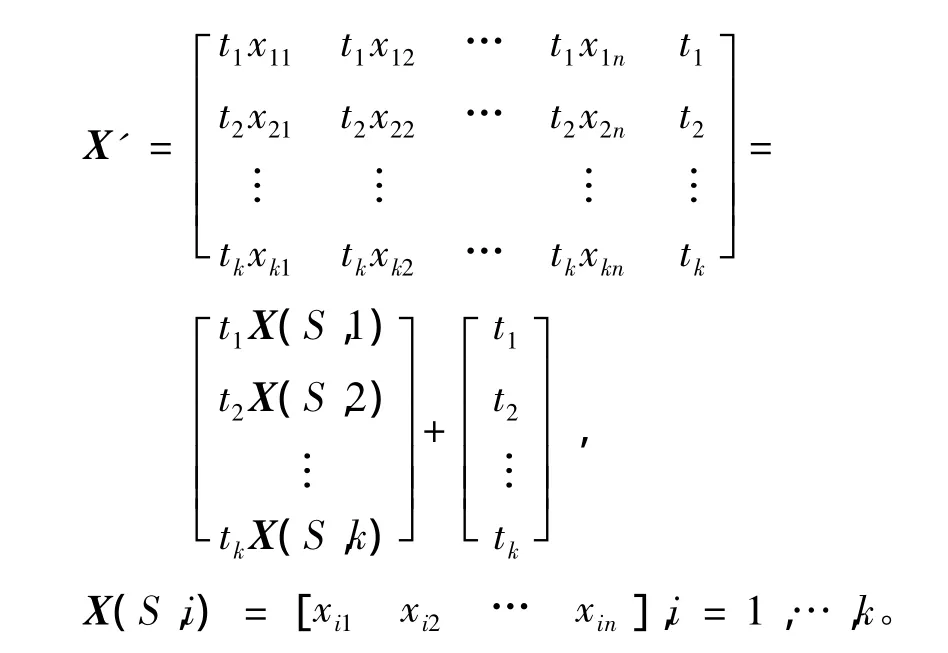
信宿的译码方法:首先运用X'=ZM－1将源信息变换后的消息 X'译出，可以得到t1，t2，…，tk，从而可以得到对角矩阵T，然后，信宿对去掉冗余后得到的信息左乘T－1，就可得到原始的源信息X。

3 结束语

长久以来通信网络的安全问题一直受到人们的关注，污染攻击和搭线窃听攻击是威胁网络安全的主要方式。窃听与污染不同，它不能够被检测到，抗击这种攻击的重点在于防范。防窃听的安全网络编码具有广泛的发展前景。本文最后提出的改进的线性网络编码代数构造方法，虽然很好地解决了网络在窃听情况下的安全问题，但是该编码方法在应用于大型网络拓扑结构时，编码复杂度较高，如何降低其编码复杂度，还有待进一步研究。

［1］CAIN，YEUNG R W.Secure network coding［C］//In IEEE International Symposium on Information Theory.Lausanne，Switzerland:IEEE Press，2002:323.

［2］JAIN K.Security based on network topology against the wiretapping attack［J］.IEEEWireless Communications，2004，11（1）:68-71.

［3］ BHATTAD K，NARAYANAN K R.Weakly secure network coding［C］//Proceedings of FirstWorkshop on Net-work Coding.Italy:IEEE，2005.

［4］ LIMA L，MEDARD M，BARROS J.Random linear network coding［C］//IEEE International Symposium on Information Theory.France:IEEE Press，2007:546-550.

［5］ LISY R，YEUNG RW，CALN.Linear network coding［J］.IEEE Transactions on lnformation Theory，2003，49（2）:371-381.

［6］ KOETTER R，MEDARD M.Beyond routing:An algebraic Approach to network coding［C］//Proceedings of Twenty-First Annual Joint Conference of the IEEE Computer and Communications Societies.Massachusetts:IEEE Press，2002:122-130.

［7］赵慧，卓新建，陆传赉.一种基于网络拓扑的安全网络编码算法的分析［C］//中国通信学会青年工作委员会主编，通信理论与技术新发展——第十三届全国青年通信学术会议论文集，北京:国防工业出版社，2008:844-846.

ZHAO Hui，ZHUO Jian-xin，LU Chuan-lai.Analysis of algorithms for security network coding based on network topology［C］//Youth Committee of Chinese Institute of Communications.Communication Theory and New Technology Development-the Thirteenth National Conference on Youth Communication Proceedings.Beijing:National Defense Industry Press，2008:844-846.

［8］ 赵慧.安全网络编码的研究［D］.北京:北京邮电大学，2009.

ZHAO Hui.Research on secure network conding［D］.Beijing:Beijing University of Posts and Telecommunications，2009.