开关度分布:一种改进的LT 数字喷泉编码度分布

雷维嘉，刘慧锋，谢显中

（重庆邮电大学个人通信研究所，重庆 400065）

0 引言

数字喷泉码的概念最初是由 M.Luby等［1］在1998年提出的，它是一种基于删除信道的稀疏图编码，但当时只提出了这一概念，并未给出具体的实现方法。M.Luby［2－3］2002 年提出的 LT 码是数字喷泉码的第一种可实用的喷泉码。LT码编译码算法简单，译码开销很低，但在LT码中有可能出现少数源数据包没有与编码数据包中的任何一个相关联的情况。Raptor码［4］是数字喷泉码的另一种实现方法，它通过内外码级联编码的方式实现，外码是普通的纠错码，内码为弱化的LT码，从而进一步降低了编译码复杂度，同时可以提高其性能。文献［5］给出了一种RS数字喷泉码的迭代译码算法。

假设编码器的原始消息由k个数据包组成，LT码具体的编码过程［2－3］为根据某一度分布函数产生每个编码数据包的度d，LT编码器从k个源数据包中随机地选择d个数据包，组成编码数据包的候选编码数据包子集，再将它们进行异或（XOR）运算，即得到一个编码数据包。根据需要编码器不断重复上述过程，可以产生无限长的编码数据包序列。译码器采用置信传播译码算法［2－3］进行 LT译码。译码过程是从度为1（d=1）的编码数据包开始的，由其可直接得到源数据包，然后将它从其他与它相关联的编码数据包中移除（进行XOR运算）。移除后这些编码数据包的度减1。重复这一过程，直到译出所有的源数据包或没有度为1的编码数据包。可见，低度的编码数据包在译码过程中起到很重要的作用，度为1和其他低度的编码数据包的数量决定了译码过程是否能开始并持续下去，是能否成功译码的关键。

采用数字喷泉码进行传输，译码器不需要频繁反馈重传信息，接收端只需要在收到足够多的编码数据包并成功恢复原始信息后，向编码器发送一个终止信号，从而避免了大量的反馈信息的传输。数字喷泉码可应用于广播传输、分布式存储和并行下载等［6－7］，可以提高传输效率，加快数据传输速度，提高数据传输和存储的可靠性，具有很好的应用前景。

实际的译码过程中，译码器译码成功所需要的编码数据包的数量N（＞k）与采用的编码算法有关。对于LT码，N与所采用的度分布密切相关。LT编码度分布函数的好坏直接影响编码的性能。一个好的度分布能够让接收端从尽可能少的编码数据包中恢复出所有的原始数据包。

文献［2］中最早提出了一种具体的LT编码度分布函数，称为鲁棒孤子分布（robust soliton distribution，RSD）。采用这种度分布函数进行LT编码，产生的编码数据包的平均度相对较大，可以保证尽可能少的冗余信息的传输，但它产生度较小的编码数据包的数量不够多，因而其译码过程可能发生中断，这时编码器就需要发送更多的编码数据包，恢复出所有源数据包所需的编码数据包的数量增大。文献［8］中另提出了一种LT编码度分布，称为二进制指数分布（binary exponential distribution，BED），采用这种分布，可以保证在编码过程中有足够多的度很小的数据包，使译码过程能持续进行。但是，由于其大部分数据包的度都很小，每个编码数据包所携带的原始信息相应地也比较少，容易出现冗余传输，而且可能不会覆盖完所有的源数据包。这时，译码器为了完全恢复原始信息，编码器也需要发送更多的编码数据包，编码器的传输效率及信道利用率将会降低。

为了提高译码器的译码效率，减少编码器编码数据包的传输次数，本文提出了一种改进的LT编码度分布函数，称之为开关度分布函数，它结合BED和RSD 2种度分布函数的优点，可以取得更好的编译码性能。在编码器传输编码数据包的开始阶段，采用BED分布进行LT编码，然后，根据已经发送的编码数据包的个数，编码器将LT编码度分布从BED转换到RSD。仿真结果显示，采用开关度分布函数可以提高译码器的译码效率，减少编码器编码数据包的传输次数。

1 开关度分布

为了更好地介绍开关度分布，我们首先介绍了2种LT编码常用的度分布函数—鲁棒孤子分布和二进制指数分布。在此基础上，再对开关度分布进行详细介绍。

1.1 鲁棒孤子分布

在LT喷泉译码时，每次都是从度为1的编码数据包开始，并将它从其他与它相关联的编码数据包中移除，这些编码数据包的度将会减1，然后再寻找新的度为1的编码数据包，以进行下一次迭代译码。在理想情况下，为了避免冗余，希望在每次迭代中，只有一个度为1的编码数据包，而且在每次迭代译码之后，只出现一个新的度为1的编码数据包。由此，可以得到一种理想孤子分布

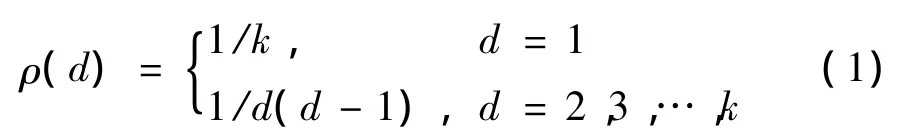
（1）式中:d表示每个编码数据包的度;k表示参与编码的源数据包数量;ρ（d）表示编码数据包度为d的概率。

在实际中，这个度分布并不理想，因为在译码过程中很可能没有度为1的编码数据包，这样，译码器的译码过程将无法进行;另一方面，在编码时，一些源数据包很可能没有被覆盖，因此，译码器就无法完全恢复出全部原始信息。

通过在理想孤子分布中引入2个额外的参数c和δ，得到另一种分布—鲁棒孤子分布。通过设计c和δ，确保译码过程中期望的度为1的编码数据包个数s大约为

（2）式中:δ为译码器未能完全恢复原始信息的概率;c为0和1之间的某一常数。

首先，定义一个正数函数

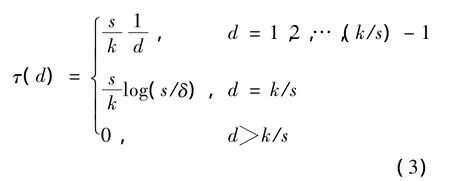
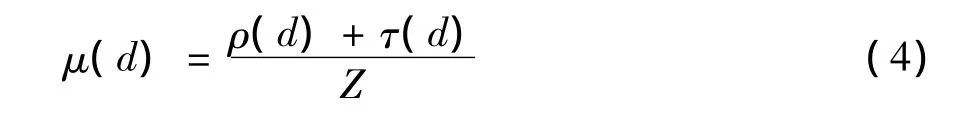
然后将理想孤子分布ρ加到τ上，再进行归一化得到鲁棒孤子分布

1.2 二进制指数分布

鲁棒孤子分布产生的编码数据包的度相对较大，编码过程中，可尽可能地覆盖所有的源数据包。但它产生的度较小的编码数据包较少，译码过程可能产生中断。为了解决这一问题，二进制指数分布增加了小度的概率，其表达式如下

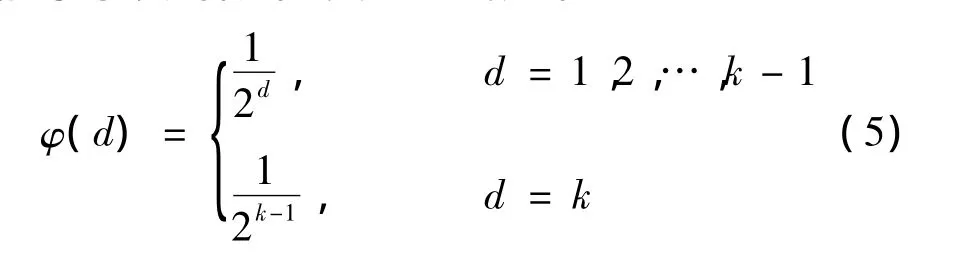
（5）式中:d表示每个编码数据包的度;k表示参与编码的源数据包数量;φ（d）表示采用二进制指数分布进行编码时，编码数据包度为d的概率。

1.3 开关度分布

在编码数据包传输的开始阶段，译码器没有收到足够多的度为1和其他低度的编码数据包，因此，它不能译码度更大的编码数据包，这时，减小编码数据包的度可以增加译码概率，可以减少译码所需要的编码数据包。因此，在编码器传输编码数据包的开始阶段，发送度较小的编码数据包，可以保证译码器在译码的过程中有足够多的度为1和其他低度的编码数据包，译码器可以更早地开始译码过程。

当发送了一定数量度较小的编码数据包后，将为译码器提供了足够多的度为1和其他低度的编码数据包，这时，如果编码器仍发送度很小的编码数据包，译码器将会收到很多冗余的数据包。译码器就需要更多的喷泉编码数据包才能够译码出所有的源数据包。如果增加编码数据包的度，可以减少冗余数据包的数量，增加覆盖所有源数据包的概率，从而可以减少编码数据包的传输次数。

根据以上分析，将BED和RSD这2种度分布函数进行组合，给出了一种LT编码开关度分布函数 ϖi，k（d），其表达式如下

（6）式中:ϖi，k（d）为采用开关度分布进行编码时，编码数据包度为d的概率;φ（d）为 BED分布;μ（d）为RSD分布;k为参与编码的源数据包的数量;α为开关点;i表示第i个喷泉编码数据包。

编码器进行LT编码时，采用开关度分布，前αk个喷泉编码数据包的度服从φ（d），保证接收端能收到足够多的度很小的编码数据包;后面的喷泉编码数据包的度服从μ（d），以减少冗余信息的传输。由此可见，开关点α的设定直接影响编码器发送编码数据包的次数，如果α设定太小，译码器未能收到足够多的度较小的编码数据包，这样，在译码时，可能没有度为1的编码数据包，译码过程无法持续下去;如果α设定太大，传输过程中的冗余信息可能会大大增加。对于这2种情况，译码器为了恢复原始信息，编码器都需要发送更多的编码数据包。从理论上推导出最佳开关点α的值比较困难，我们通过仿真的方法，给出当α取不同值时，对于不同的源数据包数量，译码器成功译码时，编码器需要发送的编码数据包数量来得到最佳的开关点。

图1为参与编码的源数据包数量k变化时，编码器发送的编码数据包的数量随开关点α的变化情况。仿真中，取开关点α的变化步长为0.05，对每个源数据包数量k做30次蒙特卡洛仿真，取其平均值。从仿真结果可以看到，α=0.1是最佳开关点，此时编码器发送的编码数据包数量是最少的。

2 仿真结果

我们通过仿真验证开关度分布的性能，并与鲁棒孤子分布和二进制指数分布进行性能比较。在仿真中，编码器将编码后的数据包发送给译码器，假设传输过程中数据包没有丢失。在仿真过程中，RSD分布中的参数c和δ分别取0.5和0.03，每个数据包的比特长度为100，译码器采用置信传播译码算法［2］来进行 LT 译码。

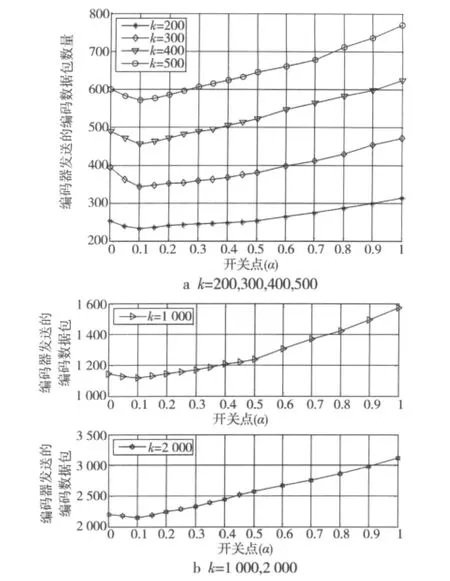
图1 参与编码的源数据包数量变化时，编码器发送的编码数据包数量与开关点α的关系Fig.1 Number of transmitted encoded packets for different switch point and different number of source packets

当编码器原始数据包数量k=1 000时，采用3种不同的度分布进行LT编码时，译码器成功译码的源数据包的比率与正确接收的编码数据包的数量之间的关系如图2所示。从图2中可以看出，开关度分布与鲁棒孤子分布相比，当译码器正确接收到的编码数据包较少时，采用开关度分布进行编码，译码器成功译码的源数据包的比率更大，即译码器能译出的源数据包更多。而且采用开关度分布，译码器的译码时延更小。与BED分布相比，采用开关度分布时，接收到少量的编码数据包时，译码器成功译码的源数据包的比率较小，但随着接收到的编码数据包数量的增加，其比率值上升更快，当收到1 080个编码数据包时，将大于BED分布的比率值。另外，采用开关度分布，译码器成功恢复原始信息所需要的编码数据包更少。

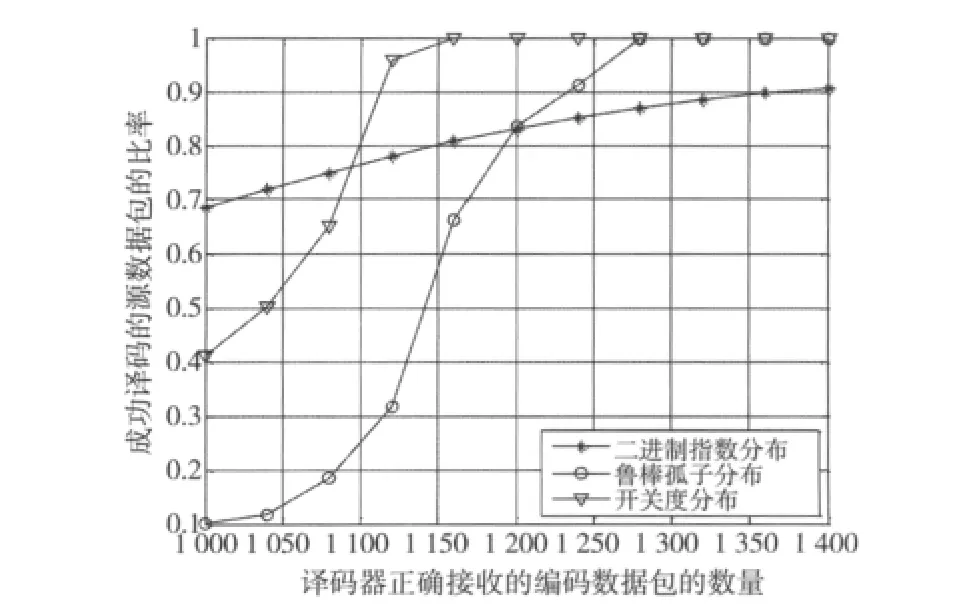
图2 当k=1 000时，译码器成功译码的源数据包的比率与正确接收的编码数据包的数量的关系Fig.2 When k=1 000，the ratio of recovered source packets with different number of the encoded packets successfully received by the destination

译码效率η表示编码器发送信息的数据包数量k与译码器成功译码时编码器所发送的编码数据包的数量N的比值，即η=k/N（0＜ η≤1），译码效率越接近于1，度分布函数性能越好。图3给出当源数据包数量变化时，译码器要成功译码原始信息，编码器需要发送的编码数据包数量。从图3中可以看出，对于不同数量的源数据包，当采用开关度分布进行LT编码时，与鲁棒孤子分布和二进制指数分布相比，译码器成功译码时，需要接收的编码数据包数量都有一定程度的减少，译码效率更高。

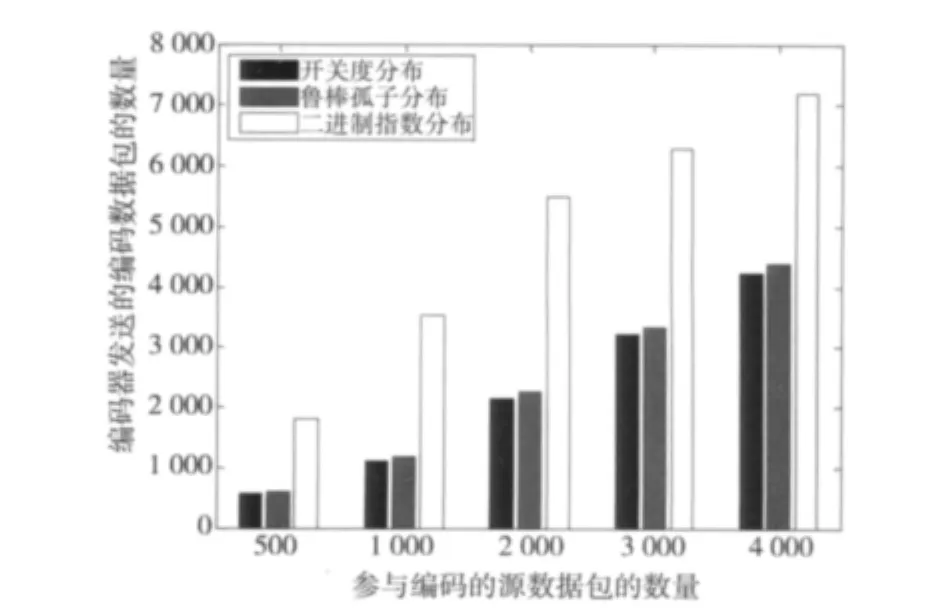
图3 参与编码的源数据包数量变化，译码器成功译码时，编码器发送的编码数据包数量Fig.3 Number of the transmitted encoded packets from the source to the destination，the number of the source packets is variable

从图3中可知，采用BED分布进行编码时，译码器的译码效率比采用RSD分布和开关度分布时的译码效率都要差很多。为了更清楚地说明开关度分布与RSD分布的区别，图4给出了当编码器原始数据包数量k变化时，编码器采用RSD和开关度分布进行LT编码时，译码器的译码效率。从图4可以看出，采用开关度分布进行LT编码，译码器的译码效率总要高于采用RSD分布时的译码效率，即译码器成功译码时，编码器发送的编码数据包更少。

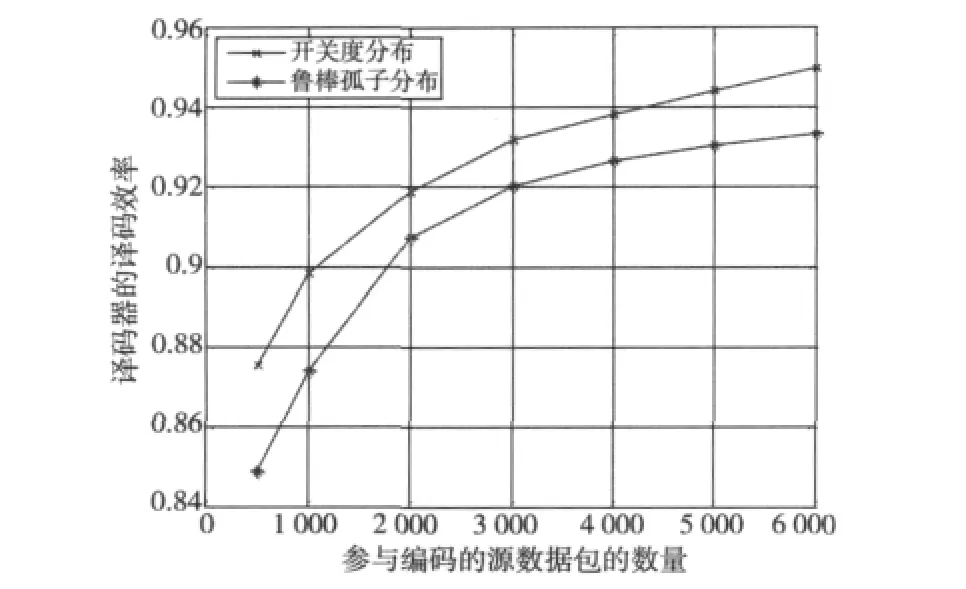
图4 参与编码的源数据包数量变化时，译码器的译码效率Fig.4 Decoding efficiency of the destination when the number of the source packets is variable

3 总结

本文中我们提出了一种改进的LT数字喷泉码度分布:开关度分布，它综合了RSD和BED这2种度分布的优点，既可以产生足够多的度较小的编码数据包，又尽可能地覆盖所有的源数据包。通过仿真得到，当开关点为0.1时，译码器成功恢复原始信息所需的编码数据包数量最少。仿真结果显示，与

RSD和BED这2种度分布相比，其性能都有明显的改善。在今后的工作中，将进一步从理论上推导证明开关点的取值。

［1］ BYERS J，LUBY M，MITZENMACHER M，et al.A digital fountain approach to reliable distribution of bulk data［J］.ACM SIGCOMM Computer Communication Review，1998，28（4）:56－67.

［2］LUBY M.LT codes［C］//Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science（FOCS），2002.USA:IEEE Press，2002:271－280.

［3］MACKAY D.Fountain codes［J］.IEEE Communications Proceedings，2005，152（6）:1062－1068.

［4］ SHOKROLLAHIA.Raptor codes［J］.IEEE Transactions on Information Theory，2006，52（6）:2551－2567.

［5］雷维嘉，张鑫，谢显中.一种迭代方法的RS喷泉码的编译码算法［J］.重庆邮电大学学报:自然科学版，2010，22（3）:308－311.

LEIWei－jia，ZHANG Xin，XIE Xian－zhong. Iterative coding and decoding algorithm of RS fountain code［J］.Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition，2010，22（3）:308－311.

［6］ BYERS J，LUBY M，MITZENMACHER M.A Digital Fountain Approach to Asynchronous Reliable Multicast［J］.IEEE Journal on Selected Areas in Communications，2002，20（10）:1528－1540.

［7］ MITZENMACHER M.Digital Fountains:A Survey and Look Forward［C］//IEEE Information TheoryWorkshop.USA:IEEE Press，2004:271－276.

［8］ AGHA K，STOJMENOVIC I.Fountain Code with XOR of Encoded Packets for Broadcasting and Source independent backbone in Multi－hop Networks using Network Coding［C］//Vehicular Technology Conference， VTC－2009.USA:IEEE Press，2009:1－5.