需求依赖库存量的变质性物品供应链协调

2012-06-05杨志林

合肥工业大学学报（自然科学版） 2012年2期

陶胜，杨志林，宋辉

（合肥工业大学数学学院，安徽合肥 230009）

0 引言

随着全球经济的发展，企业之间的竞争越来越激烈，为了追求利益最大化，生产商与销售商之间就需要协调，近年来，人们越来越重视这种协调问题，主要讨论生产商在制定整个协调机制中起主导地位，研究在保证销售商总利益不受到损失的条件下使其利益最大化，同时，使得整个供应链的利益都得到提高。然而对于库存水平影响需求的供应链协调问题的研究却不多，文献［1］最早建立了由1个生产商和1个销售商或2个相互竞争的销售商组成的供应链协调模型，并给出了货架线性补贴的协调策略；文献［2－3］分析了销售商进货决策和货架决策不同顺序的供应链协调问题；文献［3］给出了回购加线性补贴的协调策略。文献［1－3］都是从市场营销的角度考虑供应链协调问题，没有考虑销售商的库存持有成本和订货周期。文献［4－8］大多没有考虑变质问题，或者从某一方的角度来研究库存问题，或者不涉及协调问题。

本文主要考虑由单个生产商与单个销售商组成的两层非一体化供应链协调问题，在假设生产商生产的商品具有易变质性及生产率无限大且需求率受销售商当前的库存水平影响的前提下，研究了由单个生产商与单个销售商组成的供应链量折扣下的协调问题。该供应链模型主要是讨论生产商如何设计价格折扣策略来吸引销售商增加订货量，问题的分析基于Stackelberg主从博弈，即生产商是决策者，制定其价格折扣计划，而销售商是决策的跟随者，将依据主导者的决策来确定自己的订货量决策。对于生产商做出的不提供量扣折和提供量扣折这2种情形决策，分别给出了生产商的最优折扣率、最优供货量和销售商的最优批货量，从理论上分析了模型最优解的存在性和唯一性，并提供了相应的求解方法。

1 模型的记号与假设

（1）在整个过程中，生产商是主导方，其了解市场信息（包括市场需求以及销售商的各项成本），在一个周期里销售商一次补充商品，系统运行在无限周期水平下，且不考虑缺货情形。

（2）在销售过程中，需求率依赖于当前的库存水平，即

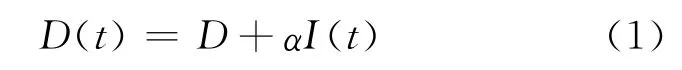
其中，D≥0；α≥0；I（t）表示t时刻的库存水平。

（3）商品的变质率θ假定为一个常数，且商品变质后无残值。

（4）T表示一个订货周期的长度；Q表示每个订货周期的订货量；由于生产商是一次性供货给销售商的，c表示生产商销售Q个商品每个商品的平均成本（这里包括变质的物品费用、库存费用、生产成本）；p表示单位商品的市场售价；w表示销售商的单位商品的进价。

（5）Ar表示销售商每次订货的固定订货费用；Am表示生产商每次生产的准备费用；hr表示销售商单位时间单位商品的库存费用。

（6）TPr、TPm分别表示未实施量折扣计划时销售商、生产商的平均利润；TPdr、TPdm分别表示实施量折扣计划后销售商、生产商的平均利润。

（7）L表示销售商愿意改变其原有的经济批量时可获得的最少利润增量的百分比。

2 销售商与生产商协调运作

根据假设，销售商的库存水平变化的微分方程可表示为：

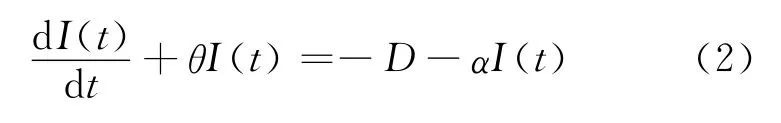
由于I（T）＝0，得

其中，b＝α＋θ。

由初始值I（0）＝Q，知

由于计算比较复杂，可以利用Pade逼近求出T的近似值，而Pade逼近较Taylor级数展开精确，其结果较接近真实值，由Pade逼近可知：

2.1 双方联合运作的决策

若生产商也有自己的零售部或者双方通过协商形成一个联合公司，那么这样的一个联合公司在T时间里的平均利润为：

将（1）式、（3）式、（5）式代入（6）式，可得：

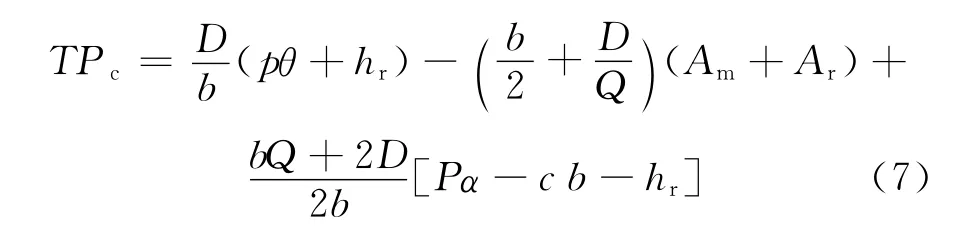
当Q∈（0，＋∞）时，有

TPc是关于变量Q的上凸函数，因此联合运作时存在唯一最优订货量Q＊c，使得方程为：

2.2 生产商与销售商各自独立运作的决策

若双方各自独立决策，遵从以生产商为主的Stackelberg博弈，即生产商是核心企业，处于主导地位，而销售商处于从属地位，因此生产商要了解销售商在哪个价格下能使进货量达到最多，从而确定其最优价格。而销售商根据生产商给定的批发价格w来确定最优订货量Q＊r，使其利润最大化。

在一个周期内销售商的平均利润函数是：

将（1）式、（3）式、（5）式代入（9）式，可得：

同理，当Q∈（0，＋∞）时，有

即TPr也是关于变量Q的上凸函数，则当∀w＞max｛pα－hr／b，0｝时，销售商存在唯一的最优订货量Q＊r，必满足方程：

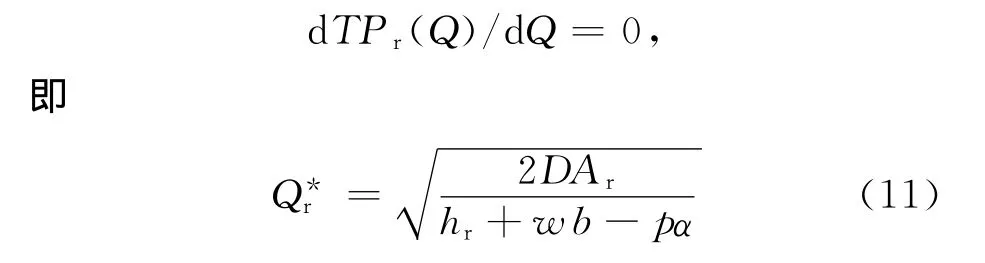
而此时生产商的平均利润函数为：

将（5）式代入（12）式，可得：

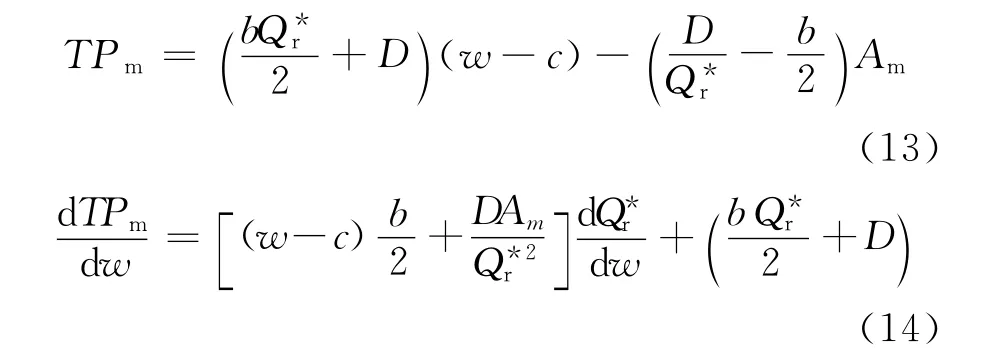
再由（11）式，得

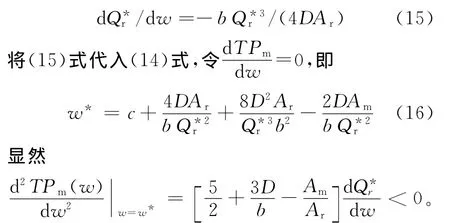
所以w＊为TPm（w）的最优值，这样可相应地算出TP＊m、TP＊r。

2.3 联合运作与独立运作的结果比较

定理1 在联合运作下的最优订货量Q＊c总大于以生产商为主的Stackelberg博弈下的销售商最优订货量Q＊r，即Q＊c＞Q＊r，且TPc＞TP＊m＋TP＊r。

2.4 协调双方的量折扣模型

由于生产商和销售商之间遵循以生产商为主导的Stackelberg博弈，此时生产商给销售商的价格为w＊，销售商的订货量为Q＊r。若生产商想提高自己的平均利润同时也提高销售商的利润，生产商就得提供价格折扣，吸引销售商增加订货量，假设生产商给销售商的价格折扣如下：

其中，r为价格折扣因子（0＜r＜1）；k为销售商订货量是原有订货量的倍数（k＞1），且这2个变量是决策量。

销售商有2种选择，即按正常价格或者是接受折扣但需其利润至少增加L%。下面给出折扣下的双方平均利润。销售商的平均利润函数为：

生产商的平均利润函数为：

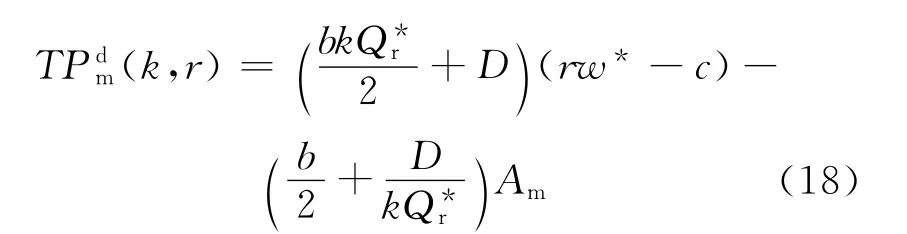
解下列约束条件下的优化问题：

而生产商只会满足销售商的最低要求，即

将（17）式代入（20）式，得

将（21）式代入（18）式，得

k在（1，＋∞）上存在唯一实根k＊，使得：

k被唯一确定，从而r也被唯一确定。又因为在量折扣条件下生产商的平均利润也增加，即

因此，当L∈（0，L＊）时，必有0＜r＊＜1，即k＊、r＊均为所求。

定理2 在此量折扣（k＊，r＊）下，当L∈（0，L＊）时，销售商的最优订货量k＊Q＊r＝Q＊c，即此时供应链实现整体最优，生产商和销售商都提高了平均利润。

证明由（8）式和（24）式得k＊Q＊r＝Q＊c，又由在之前的模型中可知，当销售商的最优订货量达到Q＊c时，整个供应链实现了整体最优。又根据在量折扣下模型的假设，当L∈（0，L＊）时，生产商和销售商都提高了平均利润，证毕。

上述模型说明了生产商可以通过一些策略来提高整个供应链的利润，使供应链实现了完美的协调。

3 应用实例

为说明上述模型的求解过程及相关结论的现实性，现给出一个具体的算例。D（t）＝200＋0.1I（t），即D＝200，p＝15，c＝8，Am＝550，hr＝0.4，Ar＝50，θ＝0.1，α＝0.1。

利用Matlab7.8，可求出Stackelberg主从博弈下销售商的原始最优订货量Q＊r＝417.681，制造商提供的正常批发价格为w＊＝10.880 3。而系统的最优订货量为Q＊c＝1 483.2，可见供应链并没有达到最优状态，所以作为主导者制造商必须采取合适的策略来协调整个供应链，以获得更高的利润。可以计算L＝0.238 8，则可算得最优解为K＊＝3.551 0，r＊＝0.876 2。即制造商提供的最优量折扣计划为：如果销售商的总订购量小于原始最优订货量的3.551 0倍，则提供正常批发价格10.880 3；否则提供折扣。

下面分析销售价格的变化给供销双方所带来的影响，见表1所列。