受线性载荷作用的含加强圆环无限大板解析解

李 昊， 刘一华

（合肥工业大学 土木与水利工程学院，安徽 合肥 230009）

由于几何不连续而在孔边产生的应力集中往往是含孔结构失效的主要因素，因而确定孔边的最大应力并采取措施予以加强一直是人们十分关注的课题［1－6］。在孔的内侧粘贴异质加强环（层）是一种减小孔边应力集中的有效方法，并在工程中得到广泛应用。求得这类问题的闭合解，有助于合理选择加强环（层）的材料及其厚度，从而可获得降低应力集中的最佳效果。为此，人们采用各种方法对此类问题进行了分析和计算。文献［2］采用Airy应力函数法分析了此类问题，并获得了加强环的最佳刚度和厚度。文献［6］利用保角映射和解析延拓方法，得到了含椭圆孔无限大体在孔内粘贴了加强层并在远端受均匀载荷作用时的级数解。然而，对于工程中常见的非均匀载荷作用情况的研究尚不多见。

本文采用复变函数方法分析在远端受双轴线性载荷作用的含圆孔并在孔的内侧粘贴异质加强圆环的无限大板，讨论加强圆环的材料属性和厚度对板的孔边最大应力的影响。

1 解析解

分析模型如图1所示，加强圆环的内、外半径分别为R0和R1，板远端作用的线性载荷分别为p1＝a＋by和p2＝c＋dx。对于平面问题，极坐标系下的应力σr、σθ、τrθ和位移ur、uθ可以用2个复势函数φ（z）和ψ（z）［7］表示为：

其中，z＝reiθ为复变量；横杠表示共轭；撇号表示求导；μ为切变模量；κ为弹性常数，对于平面应力问题κ＝（3－ν）／（1＋ν），对于平面应变问题κ＝3－4ν；ν为泊松比。

图1 分析模型示意图

板的远场（r→∞）应力边界条件为：

加强圆环内侧边界L0（r＝R0）处的应力边界条件为：

应力和位移在界面L1（r＝R1）处的连续条件为：

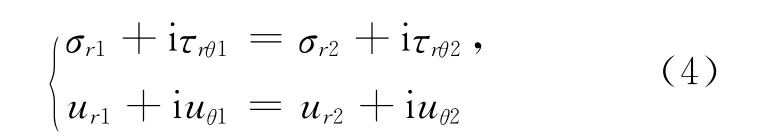
（2）～（4）式中的下标1和2分别表示板和加强圆环。

取板的复势函数φ1（z）和ψ1（z）为：

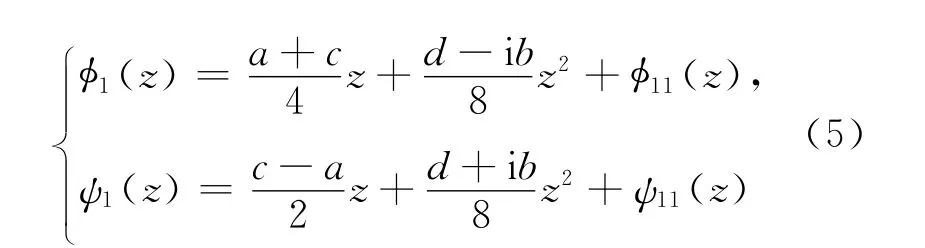
其中，φ11（z）和ψ11（z）为待定的复势函数。将加强圆环的复势函数φ2（z）和ψ2（z）展开为Laurent级数［8］，即

然后，分别将（5）式和（6）式代入（1）式，考虑边界条件和连续条件（2）～（4）式，（5）式中的复势函数φ11（z）和ψ11（z）以及（6）式中的系数ak和bk可以利用Cauchy积分求出［8］。为简便起见，计算过程不再给出。由此可求得板和加强圆环中的应力分别为：

2 数值验证

应用本文得到的解析解计算板和加强圆环内的应力并与用有限元分析软件MSC.Nastran得到的数值结果进行比较，如图2所示。

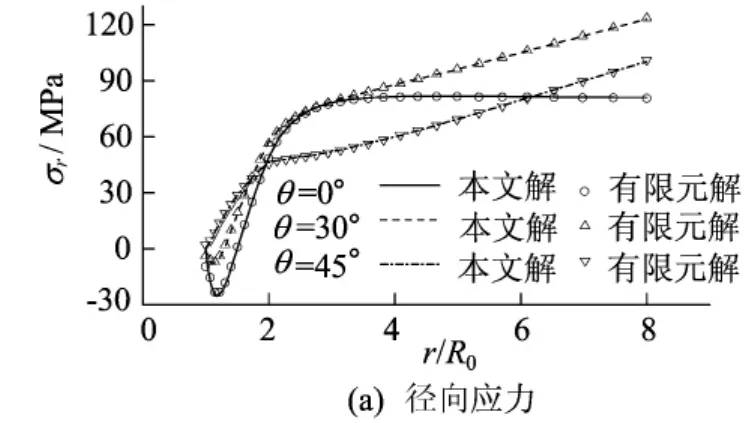
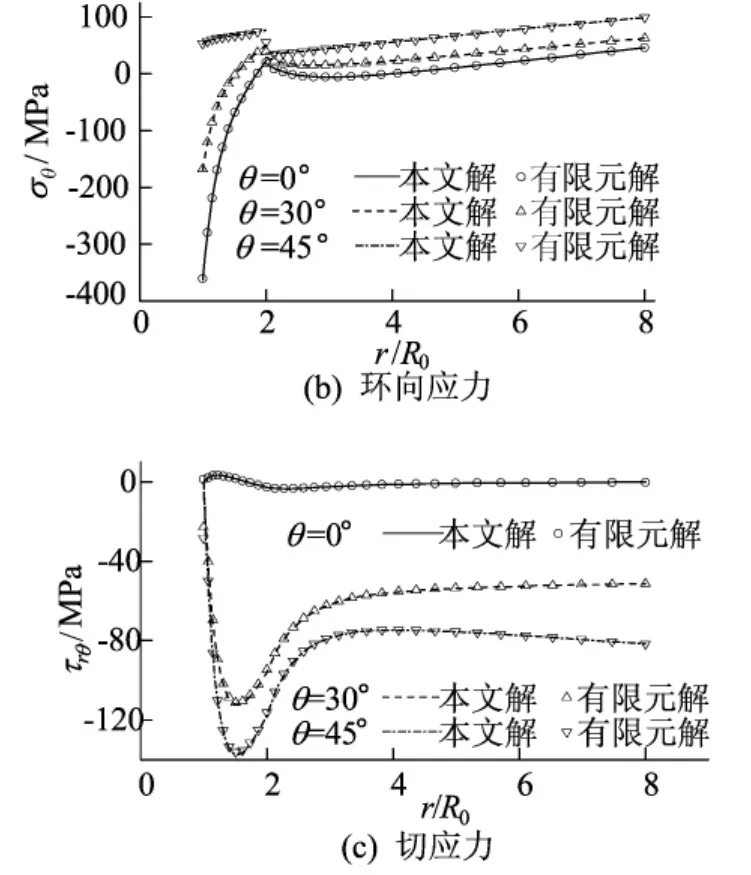
图2 不同方向应力的解析解与有限元解的比较

加强圆环的内半径为R0＝6mm，外半径为R1＝12mm，板和加强圆环的材料参数分别为μ1＝27GPa、μ2＝78GPa和ν1＝ν2＝0.3，施加在远端的载荷为p1＝80＋3y和p2＝－50＋2x，p1和p2的单位为MPa。由图2可以看出，本文得到的解析解与有限元解十分吻合，从而验证了（7）式和（8）式的正确性。

3 结果与讨论

切变模量比Γ对板的孔边（r＝R1）处最大应力及其发生位置的影响，如图3所示。

图3 切变模量比对最大应力及其发生位置的影响

图3中板和加强圆环的泊松比均为0.3，加强圆环的内外径比为α＝0.5。

由图3a可以看出，最大径向应力和最大切应力随Γ单调递增，但是当Γ＞3时，最大切应力的增加明显变缓且最终基本不再变化。当Γ较小时，最大周向应力随Γ的增加迅速减小，当Γ＝4时达到最小值，其后则随Γ缓慢增加。因此，可以找出加强圆环和板的最佳刚度比来减小板在孔边处的最大周向应力。

由图3b可以看出，当Γ增加时，最大径向应力对应的θr0从大约32°缓慢减小到16°，而最大切应力发生的位置保持不变，即θrθ0＝135°。最大周向应力发生位置的变化完全不同。当Γ＜3时，θθ0从90°缓慢减小；当3＜Γ＜5时，迅速从大约80°减少到22°；当Γ＞5时，变化又不明显了。

板的孔边界处无量纲最大应力及其发生位置与加强圆环和板的弹性常数比κ2／κ1之间的关系，如图4所示，此时，Γ和α分别取2.9和0.5。可以看出，最大径向应力和最大切应力随κ2／κ1单调递减，而最大周向应力则随κ2／κ1单调递增，3个最大应力基本上与κ2／κ1成线性关系。除了最大周向应力发生的位置θθ0随κ2／κ1的增加而略微增大外，另2个基本不变。总体而言，κ2／κ1对最大应力的影响没有Γ显著。

图4 弹性常数比对最大应力及其发生位置的影响

板的孔边界处的无量纲最大应力及其发生的位置与加强圆环内外径比α的关系如图5所示。此时，切变模量比为Γ＝2.9，板和加强圆环的泊松比均为0.3。

由图5可以看出，对于最大径向应力，当α＜0.65时，随α递减；当0.65＜α＜0.83时，随α的增加而增大；当α＞0.83时又随α的增加而减小；当α＝1时（即退化为无加强圆环的情况），最大径向应力为0；当α较小或较大时，其发生的位置变化很小，而当0.4＜α＜0.8时则迅速从15°增大到87°。

图5 加强环内外径比对最大应力及其发生位置的影响

对于最大周向应力，当α＜0.5时，加强圆环厚度的影响可以忽略不计，而α＞0.5时，则随α的增加迅速增大；其发生的位置变化不明显，基本在81°～91°之间变化。最大切应力的变化趋势基本上和最大周向应力相反，当α＜0.68时，随α缓慢递增；而当α继续增加时则迅速减小；其发生的位置保持135°不变。由此可以看出，当加强圆环的内外径比为0.5左右时，对板孔口的加强效果最佳。

4 结束语

本文采用复变函数法求得了含圆孔的无限大板孔内粘贴异质加强圆环在远端施加双轴线性载荷的解析解，讨论了加强圆环的材料性能和厚度对板孔边处最大应力的影响。结果表明，选择合适的加强圆环的材料和厚度可以显著降低板孔边的最大应力，从而达到优化设计的目的。

［1］Theotokoglou E N，Tsamasphyros G J.Stress concentration for a circular hole in a strip by singular integral equations［J］.Mechanics Research Communications，1986，13（4）：221－229.

［2］Chau K T，Wei X X.Stress concentration reduction at a reinforced hole loaded by a bonded circular inclusion ［J］.Journal of Applied Mechanics，2001，68（3）：405－411.

［3］Tse P，Lau K，Wong W.Stress and failure analysis of woven composite plates with adhesive patch－reinforced circular hole［J］.Composites Part B：Engineering，2002，33（1）：57－65.

［4］Yavari V，Rajabi I，Daneshvar F，et al.On the stress distribution around the hole in mechanically fastened joints［J］.Mechanics Research Communications，2009，36（3）：373－380.

［5］汪鹏程，胡 成，朱朝辉.有初始原岩应力的弹粘塑性岩土介质中圆柱形孔扩张问题解析解［J］.合肥工业大学学报：自然科学版，2009，32（10）：1462－1465.

［6］Chao C K，Lu L M，Chen C K，et al.Analytical solution for a reinforcement layer bonded to an elliptic hole under a remote uniform load ［J］.International Journal of Solids and Structures，2009，46（14／15）：2959－2965.

［7］徐芝纶.弹性力学：上册［M］.第4版.北京：高等教育出版社，2006：73－92.

［8］路见可.平面弹性复变方法［M］.第3版.武汉：武汉大学出版社，2005：65－89.