全相位FRM陷波原理及其DSP Builder实现

吕 卫，崔海涛，黄翔东

(天津大学电子信息工程学院，天津 300072)

全相位FRM陷波原理及其DSP Builder实现

吕 卫，崔海涛，黄翔东

(天津大学电子信息工程学院，天津 300072)

为设计出陷波点可精确控制、具有高陷波深度及低硬件复杂度的陷波器，提出了一种结合频率响应屏蔽(FRM)技术与全相位滤波技术的高效陷波器实现结构．在分析双相移组合全相位陷波器陷波深度不足的基础上，指出原型滤波器和屏蔽滤波器内含的单窗全相位卷积窗是陷波深度得以大幅度增大的根本原因，理论推导出陷波器频率响应表达式，证明了在平移参数 λ取非 1/2整数倍的情况下，提出的陷波结构无需任何补偿和校正措施，其陷波深度高达约-200,dB. 借助Altera开发工具DSP Builder对所提出的陷波结构进行建模、仿真，产生Quartus Ⅱ能够识别的VHDL源程序，利用ModelSim进行RTL级仿真，综合、适配并下载至FPGA芯片．实验结果验证了设计方法的正确性和实用性．

频率响应屏蔽；全相位；陷波器；衰减特性；DSP Builder；FPGA

陷波器设计一直是学术界和工程界的难题．文献[1]指出，性能优良的陷波器设计法应具备陷波频点位置可精确控制、设计算法简单、陷波深度足够大、陷波频带窄、计算效率足够高等优点．然而，现有大多数设计法难以同时满足以上要求，如捷克学者Zahradnik[2]在快速分析设计算法(fast analytical design algorithm)的基础上，实现了陷波频点位置的任意调节，但是该算法的复杂度较高，而且还会使得陷波器的过渡带拓宽[3]．文献[4]提出的结合2个不同截止频率的零相位低通 FIR滤波器设计的零相位陷波器，对滤波器的阶数要求较高，并且陷波点处的衰减值小．Jacek[5]设计出一种品质因数可随时间改变的IIR陷波器，但也指出，影响品质因数最优参数的解析表达式无法确定，因而该设计法仍不能精确控制陷波点位置．

文献[6]提出双相移组合全相位陷波器设计法，推导出了陷波器系数的简化公式，只需将与频率位置相关的参数代入文献[6]的式(35)(即本文的式(1))就可直接设计出陷波点可精确控制的陷波器，在平移参数λ 取 1/2整数倍时，陷波深度可达到-330,dB．而在λ取非1/2整数倍的情况下，其陷波深度只能达到-60～-70,dB，这意味着陷波频点处的衰减幅值在通带幅值的千分之一以下，和可能的最大衰减量相比，还存在性能提高的空间．文献[7]在文献[6]的基础上，引入FRM技术[8]完成了高效陷波器设计，大大节省了乘法器等硬件资源．但是文献[7]仅给出了平移参数λ取1/2整数倍的陷波器设计实例，对λ取非1/2整数倍情况缺乏考虑．陷波器的性能是由滤波器频率响应函数决定的，文献[6-7]均未推导出陷波器的频率响应函数的解析表达式，对陷波性能也缺乏深度解释．另外，文献[7]没有对其高效滤波结构给予硬件验证．

本文对文献[7]的陷波器频率响应函数进一步分析，指出引入FRM措施后，平移参数λ取非1/2整数倍时，无需修正措施其陷波深度可达近-200,dB(即陷波频点处频率成分的幅值仅为通带成分幅值的10-10)，并深入阐述了FRM对陷波频点处衰减特性的作用机理，从而合理解释了文献[7]设计法能兼顾精确控制陷波频点和达到深度陷波衰减的根本原因；另外，还设计出了新的高效陷波结构，在 Matlab/DSP Builder环境下建模、仿真，并下载到 FPGA芯片EP2C70F672C6完成硬件实现．

1 双相移组合全相位陷波器的衰减特性分析

文献[6]给出双相移组合全相位陷波系数为

式中：wc(n)是前窗 f、后窗 b进行翻转卷积形成的单窗全相位卷积窗，即wc(n)=b(n)* f(-n)，n∈[-N，N]；C为 wc(n)的归一化因子[9]；频率向量 H在指定数字角频率 m×2π/N处实现陷波．将频率向量长度N、整数 m和平移参数λ 值代入式(1)就可设计出陷波点位于ω˜=(m-λ)2π/N处的陷波器，整数m实现陷波器的“粗调”，而小数λ实现陷波点的“微调”．

对式(1)的系数 g(n)进行傅里叶变换，可得陷波器的频率响应函数为

式中卷积窗wc(n)的傅里叶变换为Wc(jω)．G(jω)实际上就是将卷积窗频响函数 Wc(jω)分别朝左右方向平移得到与 Wc2(jω)=后，再用全通频响减去 Wc1(jω)与 Wc2(jω)的求和结果而得．因而卷积窗频响函数Wc(jω)直接决定了陷波器的传输特性．图 1给出了N=10的单窗全相位卷积窗幅度曲线和衰减曲线．

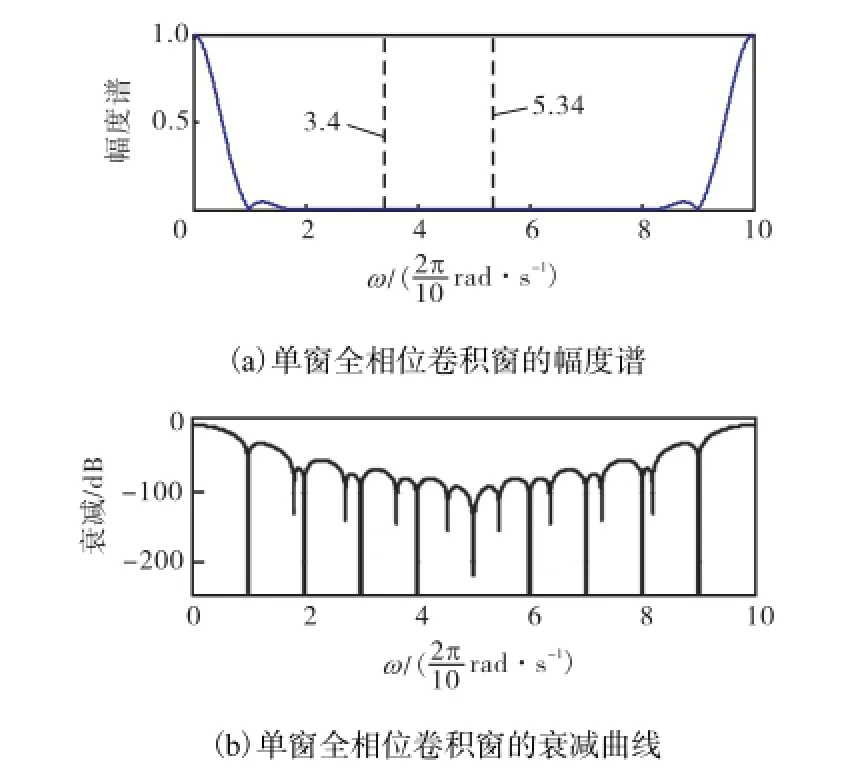
图1 单窗全相位卷积窗谱及其衰减曲线(N=10)Fig.1 Spectrum of all-phase single convolution window and its decay curve (N=10)

文献[9]指出：图 1中的单窗全相位卷积窗谱在整数倍频率采样点ω=k2π/N上满足关系

因而不妨令 N=10、m=2、λ=0.3，则根据式(3)，如图 2(a)所示，将卷积窗Wc(jω)向右平移ω˜= 1.7×2π/N后的 Wc1(jω)必然满足 Wc1(jω˜)=1；同理，如图 2(b)所示，将Wc(jω)向左平移ω˜(等价于向右平移 2π-ω˜)后的 Wc2(jω)必然满足 Wc2[j(2πω˜)]=1；联立式(2)和式(3)，则整个陷波器的传输曲线如图2(c)所示．

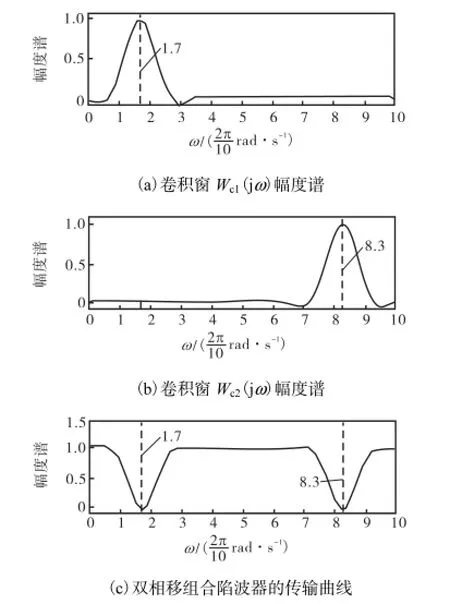
图2 双相移组合陷波器特性曲线(N,=,10,,m,=,2,,λ,=,0.3)Fig.2 Curves of double phase-shift combination notch filter (N,=,10, m,=,2, λ,=,0.3)

联立式(2)和式(3)，易推知在陷波点ω˜处

则其用分贝值表示的衰减深度值为

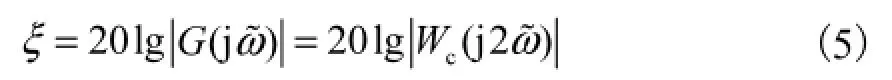
从图 1(b)可看出，在2ω˜=3.4×2,π/N处卷积窗谱的对数衰减值 20lg仅有-70,dB左右，这决定了整个陷波深度也只能达到-70,dB左右．

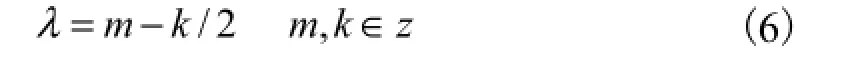
即平移参数λ取1/2整数倍时，才能使得整个陷波器获得理想无穷大的陷波深度；当 λ取非 1/2整数倍时，其陷波深度总是有限的，仅能达到-60～-70,dB(文献[9]的实验曲线证明了此结论)．

而实际工程应用如直接序列扩频、军事等许多应用场合，总是期望平移参数λ不局限于 1/2整数倍而是任意取值的．因而在λ取任意值时，如何保证足够大的陷波深度是需解决的关键问题．

2 基于 FRM技术的高效陷波器衰减特性分析

FRM 滤波结构[8]如图 3所示，它包括原型滤波器 E(z)经内插得到的 E(zM)，长度为-(N-1)M/2的延时单元，用于生成互补原型滤波器，和 2个互补的屏蔽滤波器F(z)、Fc(z)．

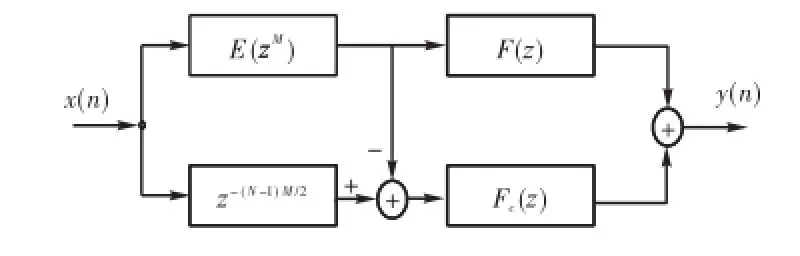
图3 FRM基本结构Fig.3 Basic structure of FRM

根据文献[7]，为设计高效陷波器，选取具有点通频率性质的单边带频率向量H和Hc，与文献[7]中将两者设置成互为偶对称形式不同的是，本文选择将两者设置成传统对称形式[9]，即

式中 wc(n)是单窗全相位卷积窗[9]．对式(8)进行傅里叶变换，得到原型滤波器的频率响应函数

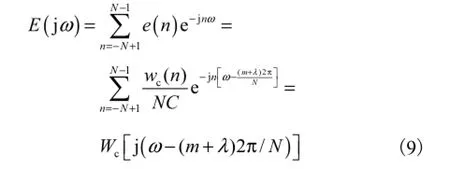
对E(jω)作内插因子为M的补0操作后，其频率响应表示为

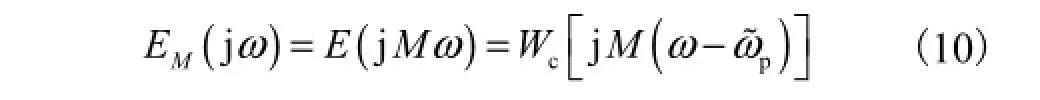
同理，选取具有点通频率性质的单边带频率向量

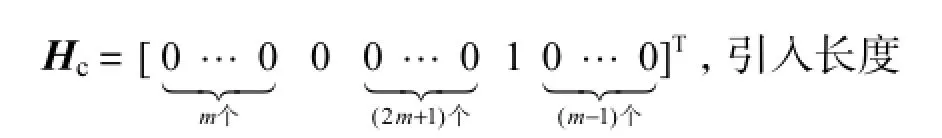
图4 高效陷波器设计过程(N=10，M=4，m=2，λ=0.67)Fig.4 Designing process of high efficiency notch filter (N=10，M=4，m=2，λ=0.67)

从图 4(a)和(b)还可看出，内插操作导致原型滤波器和互补原型滤波器产生了 M-1=3条镜像曲线，故其频响并不具备点通频率特性．因而需设计一点通滤波器以“屏蔽”这 3条镜像曲线．为“提取”出图 4(a)所示 ωp=2π/M+pω˜=3.167,5×2π/N处的频率曲线，需要设计具有点通频率特性的屏蔽滤波器，其频率响应 F(jω)与 EM(jω)的点通频率保持一致．为此，可令全相位阶数Np=2M，其单边带频率向量设置为

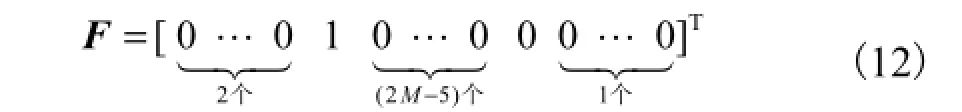
式中：Cp为归一化因子；wpc是长度为2Np-1的单窗全相位卷积窗，其窗函数谱Wpc(jω)如图5所示．

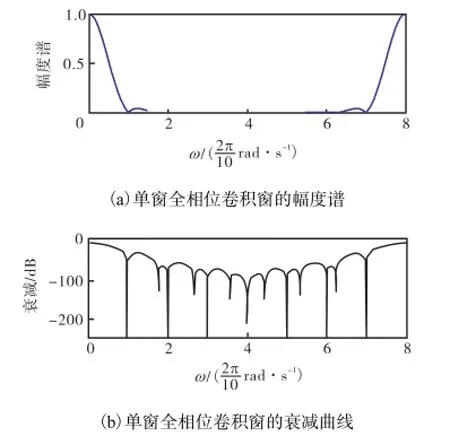
图5 单窗全相位卷积窗谱及其衰减曲线(Np,=,8)Fig.5 Spectrum of all-phase single convolution window and its decay curve (Np=8)

对式(13)的f(n)进行傅里叶变换，得到屏蔽滤波器的频率响应函数为

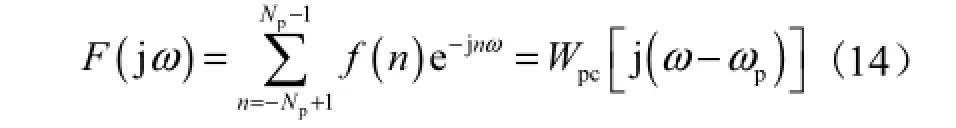
同理可求得其互补屏蔽滤波器频响为

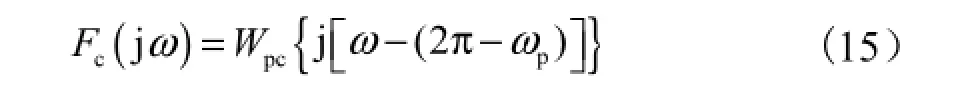
式中：Fc(jω)是由卷积窗 Wpc(jω）分别向右平移ωp、2π-ωp得到的(分别如图 4(a)和(b)所示)；ωp为高效陷波器的陷波频点．

从图4(a)和(b)可看出，经2路互补的滤波屏蔽后，获得了 2路关于 ω=π对称的点通频率曲线，其中图 4(a)的点通频响为 EM(jω)F(jω)，与之互补的图4(b)频响为EMc(jω)Fc(jω)．只需用全通频响减去

这两者之和即可得陷波频点位于 ωp处的频率响应函数P(jω)，其表达式分别为将陷波频点 ωp代入式(17)，并联立式(10)、式(11)、式(14)和(15)可得其频率响应值为

学术研究一向存在两种具有辩证色彩的现象，可以分别称为“大题小作”和“小题大做”。所谓“大题小作”，就是面对重大的、牵涉面广的研究课题，研究者要善于突出重点、提炼精华，避免巨细兼顾、失之杂芜；所谓“小题大做”，就是面对涉及的领域相对狭窄的研究课题，研究者要善于以研究对象为基点和核心做横向拓展，善于勾连和比较，使立论扎实、内涵丰厚。尚继武的专著名为《〈聊斋志异〉叙事艺术研究》，但所论内容不限于《聊斋志异》，也不限于“叙事艺术”，内容丰富，视野开阔，可以称得上是一本“小题大做”的著作。

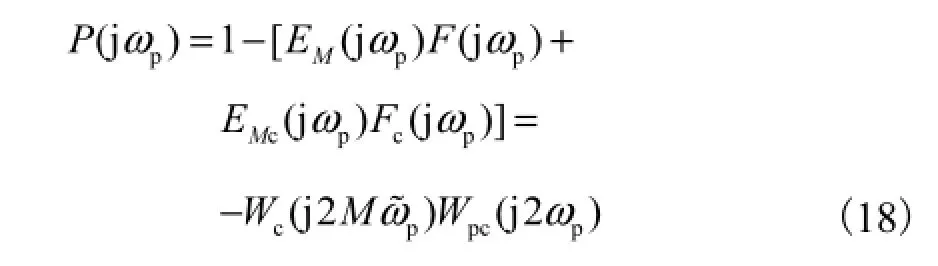
则高效陷波器在陷波频点处的陷波深度ξ为

式(19)与不引入 FRM 的式(5)相比，增添了 9项，因而增大了陷波深度．结合图1(b)与图5(b)，陷波深度等于原型卷积窗谱 Wc(jω)在 2Mpω˜=5.34× 2,π/N 处的衰减值加上屏蔽卷积窗谱 Wpc(jω)在2ωp=5.068×2,π/Np点处的衰减值．表 1给出了平移参数λ,取不同值时高效陷波器的陷波深度值．

表1 λ不同取值时高效陷波器陷波深度值(N,=,10，M,=,4，m,=,2)Tab.1 Attenuation of high efficiency notch filter with different values of λ(N,=,10，M,=,4，m,=,2) dB

从表1数据可看出，参数λ取不为1/2整数倍的任意值时，陷波深度值可达-200,dB左右．

综上所述，FRM 的引入有如下作用：①由于式(19)的陷波深度比式(5)多出1项，即由增加到因而相比于双相移组合陷波情况，进一步增大了陷波深度；②由于考虑到了将屏蔽滤波器的点通频率位置与原型滤波器点通频率保持一致，因而相比于双相移组合情况，其陷波点位置没有偏移，完全可由式(16)的参数m和λ灵活控制；③屏蔽滤波器进一步减弱了双相移组合情况的左右边带干扰；④FRM 技术需引入滤波器系数内插措施，因而原型滤波器的系数大部分是0，节省了乘法器资源，保证了陷波器硬件资源实现的高效配置．

3 高效陷波器模型仿真与硬件实现

由文献[7]得知，第1支路的原型滤波器eM(n)和屏蔽滤波器f(n)与第2支路的eMc(n)和fc(n)满足共轭关系，即

对式(17)进行傅里叶逆变换，联立式(17)和式(20)，可导出高效FRM陷波器系数p(n)为

式中：eM为原型滤波器M倍内插后的滤波器；f为屏蔽滤波器；Re()、Im()分别表示取实部和虚部操作．根据式(21)，本文提出如图 6所示易于硬件实现的高效陷波结构．由于eM滤波器系数后M-1位是0，可舍弃不用，则等效的FIR陷波器的长度L为

图6 基于FRM技术的高效陷波器结构Fig.6 Structure of high efficiency notch filter based on FRM

根据推导出的高效陷波器结构，在 FPGA开发环境 DSP Builder[10]设计高效陷波器的硬件模块．在Matlab/Simulink环境中完成模型的设计输入，即在Matlab/Simulink环境中建立一个 mdl模型文件，采用图形方式调用Altera DSP Builder和Simulink库中的模块，完成高效陷波器的系统级框图，如图7所示．

在图 7的系统级框图中，原型滤波器系数 e(n)的实部与虚部分别通过子系统 Re_y、Im_y，在内部进行M倍内插，并实现与输入数据卷积后，两子系统的输出再分别通过子系统 Re_Y、Im_Y对应与屏蔽滤波器f(n)的实部Re(f)、虚部Im(f)进行卷积；由于卷积运算采用并行加法器，使用的流水线级数 l=因此系统群延时 τ=l+(L-1)/2，代入N=10，M=4，得图 7中右下角所示的群延时τ=52．

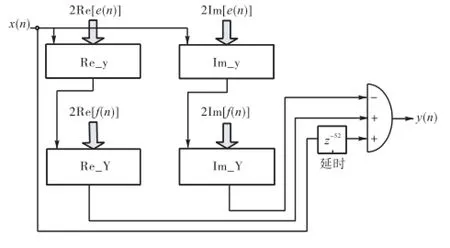
图7 基于FRM技术的高效陷波器系统级框图(N,=,10,,M,=,4,,m,=,2,,λ=,0.67)Fig.7 System-level block diagram of high efficiency notch filter based on FRM (N,=,10,,M,=,4,,m,=,2,,λ=,0.67)

为便于观察，输入频率值为与陷波频率 ωp=保持一致的正弦波(代入 N=10， M=4，m=2，λ=0.67，即得 ωp=1.990,2,rad/s，其波形如图8(a)所示)．利用Matlab计算出的陷波器系数，得到Simulink环境下的输出波形如图8(b)所示．

从图 8的仿真曲线可明显看出，系统群延时位于图8所示n=52处．将仿真数据导出到Matlab窗口，通过仿真数据可以得出：经过 2τ=104个样点的暂态间隔，其输入信号较彻底地得以滤除，这验证了高效陷波器陷波点设置的正确性；而 n＞104后的输出数据为 0，不存在振荡，这表明陷波器获得了很高的陷波深度．

建模算法仿真完成后，打开模型中的 Signal Compiler模块，设置好参数，器件选择 Cyclone系列的EP2C70F672C6，把模型转化为VHDL代码、综合以及 Quartus Ⅱ适配，同时产生 VHDL testbench文件，利用 ModelSim对生成的VHDL代码进行 RTL级仿真，仿真结果与图8一致．

把.sof文件下载到目标器件 EP2C70F672C6，输出信号接入示波器．实验结果证明与仿真结果一致．

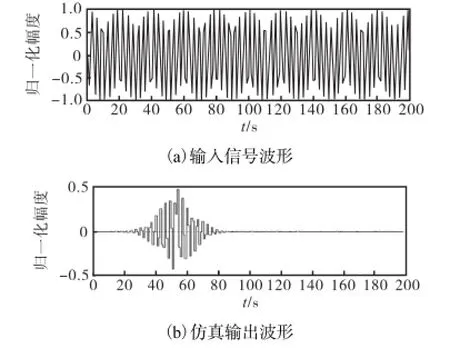
图8 高效陷波器系统级仿真(N,=,10,,M,=,4,,m,=,2,λ=,0.67)Fig.8 System-level simulation of high efficiency notch filter(N,=,10,,M,=,4,,m,=,2,λ=,0.67)

4 全相位 FRM陷波器与双相移组合陷波器的性能比较

由文献[6]得知，N阶双相移组合全相位陷波器的等效FIR长度为2N-1；根据式(22)，N阶全相位FRM陷波器的等效FIR长度为2M(N+1)-1；结合双相移组合陷波器陷波频点ω˜和全相位FRM陷波器陷波频点 ωp的公式，并代入全相位 FRM 陷波器的参数(N=10，M=4，m=2，λ=0.67)，即可求得在两者等效FIR陷波器阶数相同(L=87)的条件下双相移组合陷波器的参数(N=44，m=14，λ=0.063)．在等效阶数相同时，全相位 FRM陷波器和双相移组合陷波器的传输曲线和衰减曲线在陷波频点处的局部放大如图9所示．

图9 同等效阶数下陷波曲线比较(L,=,87)Fig.9 Comparison of notching curve under the same equivalent orders(L,=,87)

由图 9可看出，当两者的等效 FIR陷波器阶数相同时，双相移组合陷波器和全相位 FRM陷波器基本获得相同性能(表现在主陷波点 ωp=3.167,5× 2π/10处，两者获得近乎相同的过渡带宽度和陷波深度)．然而，由图 9(b)可看出，双相移组合陷波法在主陷波点附近还出现一个伪陷波点，这是由于在λ不取1/2的整数倍时，两边带的相互影响使得伪陷波点出现的缘故．而对于全相位 FRM陷波法，在图 4所示具有跟踪陷波频点的屏蔽滤波器的作用下，全相位FRM 陷波器的频率响应曲线不会出现伪陷波点，保证了陷波频点的单一性；同时，FRM的引入增大了陷波器的陷波深度(结合式(5)和式(19)即可得出)．

采用第3节高效陷波器的硬件设计流程，即可设计出 44阶双相移组合陷波器(等效 FIR陷波阶数为87)的FPGA实现．高效陷波器的FPGA资源消耗和双相移组合陷波器的资源消耗对比如表2所示．

表2 高效陷波器与双相移组合陷波器资源消耗对比Tab.2 Comparison of resource consumption between high efficiency notch filter and double phase-shift combination notch filter

分析表2两种陷波器的硬件资源消耗情况：高效FRM陷波器的基本逻辑单元消耗仅为双相移组合陷波器消耗的 30.2%，而内嵌的 9位乘法器为后者的90.7%，其中双相移组合陷波器设计过程中，由于FPGA芯片内嵌的9位乘法器资源不足，自动调用了基本逻辑单元合成乘法器，因而实际全相位 FRM 陷波器的乘法器消耗远小于双相移组合陷波器．这是因为本文设计的基于全相位FRM技术的高效滤波器系数非常稀疏，从而大大节省了乘法器数量和基本逻辑单元，降低了硬件实现的复杂度和资源消耗．

综上所述，在两者等效 FIR陷波器阶数相同的条件下，设计出的全相位 FRM 陷波器具有比双相移组合陷波器更好的传输特性和衰减特性，以及更少的硬件资源消耗．

5 结 语

本文通过对比双相移组合全相位陷波器的衰减特性，找出其陷波深度不足的根本原因，有效结合全相位滤波理论和频率响应屏蔽技术，提出简化的高效陷波器结构．并推导出高效陷波器频率响应函数的解析表达式，深刻挖掘了卷积窗函数对整体陷波性能的影响，从而阐述证明了基于 FRM 技术的高效陷波器不需任何校正和补偿措施，陷波频点处的衰减就可达到-200,dB的原因，并且其传输性能明显优于同等阶数条件下的双相移组合陷波器；为验证所提出的新型陷波结构的性能，还借助 Altera公司 DSP Builder完成高效陷波器的 FPGA实现，与相同等效阶数的双相移组合陷波器相比，基于 FRM技术的高效陷波器大大节省了乘法器数量和基本逻辑单元，设计方法简单有效，所生成的陷波器模块可移植性好．

本文所提出的方法可用于直接序列扩频系统、自适应陷波器设计等场合．

［1］ 王兆华，黄翔东. 数字信号全相位谱分析与滤波技术[M]. 北京：电子工业出版社，2009.

Wang Zhaohua，Huang Xiangdong. Digital Signal Processing Utilizing All-Phase Spectra Analysis and Filtering Techniques[M]. Beijing：Publishing House of Electronics Industry，2009(in Chinese).

［2］ Zahradnik P. Fast analytical design algorithms for FIR notch filters[J]. IEEE Trans on Circuits and Systems，2004，51(3)：608-611.

［3］ Zahradnik P，Vlcek M. An analytical procedure for critical frequency tuning FIR filters[J]. IEEE Trans on Circuits and SystemsⅡ：Express Briefs，2006，53(1)：72-76.

［4］ Satoru Kumagai，Kiyoshi Ohishi，Naoki Shimada，et al. High-performance robot motion control based on zerophase notch filter for industrial robot[C]// The 11th IEEE International Workshop on Advanced Motion Control. Nagaoka，Japan，2010：625-630.

［5］ Piskorowski J. Digital notch filter with time-varying quality factor for the reduction of powerline interference[C]// Proceedings of 2010 IEEE International Symposium on Circuits and Systems. Paris，France，2010：2706-2709.

［6］ 黄翔东，王兆华. 基于双相移组合全相位法的 FIR陷波器设计[J]. 系统工程与电子技术，2008，30(1)：14-18.

Huang Xiangdong，Wang Zhaohua. FIR notch filter design based on double phase-shift combination all-phase method[J]. Systems Engineering and Electronics，2008，30(1)：14-18(in Chinese)

［7］ 黄翔东，王兆华，吕 卫. 陷波频率点可精确控制的高效 FRM 陷波器设计[J]. 系统工程与电子技术，2009，31(9)：2320-2322.

Huang Xiangdong，Wang Zhaohua，Lü Wei. Design of high-efficiency FRM notch filter with frequency point accurately controlled[J]. Systems Engineering and Electronics，2009，31(9)：2320-2322(in Chinese)．

［8］ Lim Yong Ching. Frequency-response masking approach for the synthesis of sharp linear phase digital filters[J]. IEEE Trans on Circuits and Systems，1986，33(4)：357-364.

［9］ 黄翔东. 全相位数字信号处理[D]. 天津：天津大学电子电子工程学院，2006.

Huang Xiangdong. All-Phase Digital Signal Processing[D]. Tianjin：School of Electronic Information Engineering，Tianjin University，2006(in Chinese)．

［10］ Zeng Muhua，Wang Shisheng. The design of ECG signals dually filtering based on FPGA[C]// 2010 2nd International Conference on Industrial Mechatronics and Automation. Wuhan，China，2010：87-90.

Principle of All-Phase FRM Notching and Its Implementation Based on DSP Builder

LÜ Wei，CUI Hai-tao，HUANG Xiang-dong
(School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China)

To design a notch filter with precisely tunable notching point，high notching depth and low hardware complexity，the implementation structure of a high efficiency notch filter was proposed，which combined techniques of frequency response masking(FRM)and all-phase filtering. Based on the analysis of double phase-shift combination all-phase notch filter’s insufficient notching depth，it was pointed out that the significantly increased notching depth was essentially caused by all-phase single convolution window，which was inside prototype filter and masking filter. Moreover，the expression of notch filter frequency response was theoretically derived，and it was testified that attenuation at notching frequency could reach about-200,dB without any compensation or corrective measures，even if the shifting parameter λ was not an integer multiple of 1/2. The proposed design model was also built through running DSP Builder，where the QuartusⅡcompatible VHDL source program was generated，then register transport level(RTL)grade simulation was carried on to the model in ModelSim. After completing synthesis and specifying the pin of device，the program was downloaded to FPGA. Experimental results verified the proposed method’s correctness and practicality.

frequency response masking；all-phase；notch filter；attenuation characteristics；DSP Builder；FPGA

TN911.72

A

0493-2137(2012)04-0331-07

2010-12-14；

2011-09-08.

国家自然科学基金资助项目(60802048)；天津市应用基础及前沿技术研究计划重点资助项目(10JCZDJC16100).

吕 卫（1976— ），男，博士，副教授，luwei@tju.edu.cn．

黄翔东，xdhuang@tju.edu.cn．