基于小波及Hilbert-Huang变换提取壁湍流相干结构

2012-06-05夏振炎靳秀青

天津大学学报(自然科学与工程技术版) 2012年4期

关键词：概率密度湍流脉动

夏振炎，靳秀青，姜楠

(1. 天津大学力学系，天津 300072；2. 天津市现代工程力学重点实验室，天津 300072)

基于小波及Hilbert-Huang变换提取壁湍流相干结构

夏振炎1,2，靳秀青1,2，姜楠1,2

(1. 天津大学力学系，天津 300072；2. 天津市现代工程力学重点实验室，天津 300072)

为了研究壁湍流中的相干结构，在直流抽吸式低(变)湍流度风洞的实验段中，应用恒温热线风速仪 IFA-300精确测量平板湍流边界层不同法向位置的流向速度信号．分析壁湍流脉动速度的概率密度分布，并与高斯分布比较，验证了壁湍流中相干结构引起的猝发现象的统计规律．提出了一种利用小波变换和 Hilbert-Huang(HHT)变换相结合来提取相干结构的方法．对壁湍流脉动速度进行 HHT变换，通过变换后各模态的能量分析，分离出主要含能模态对应的相干结构．利用小波重构法继续提取未分离的小尺度相干结构．对剩余湍流信号进行概率统计，并比较提取的全部相干结构与原始湍流信号的波形和 HHT边际谱，验证了湍流信号既包含非随机的相干结构信号也包含随机的非相干信号．

Hilbert-Huang变换(HHT)；小波变换；壁湍流；相干结构；间歇性

壁湍流一直是实际流场中备受关注的热点问题，壁湍流脉动速度的概率密度分布是力学的基本问题之一．Brodkey等[1]依据实验资料分析了剪切流中湍流信号的分布，得到的脉动速度分布与高斯分布有一定偏离．Kim 等[2-3]应用直接数值模拟和大涡模拟方法对槽道湍流进行了细致的研究，得到脉动速度的偏斜度和平坦度也与正态分布不符．脉动速度概率密度分布、平坦度和偏斜度非正态分布的原因与壁面处的相干结构有关[4]．而相干结构出现在湍流信号的各种频段上，其在大尺度结构(低频部分)中表现为较典型的猝发现象，而在小尺度结构(高频部分)中同样也存在相干结构[5-6]，表现为强间歇事件．

应用小波变换中的小波系数重构法对相干结构的提取取得了较好的效果[7]．1998年，黄锷提出了经验模态分解方法(EMD)．该方法不需预设基函数就能将信号中不同尺度的波动逐级分解，产生不同特征尺度的数据序列．该方法通过波内频率调制和波间频率调制实现其非线性的分析过程[8]．研究表明，湍流信号中含能涡呈现明显的多尺度特征[9]．用 HHT分析湍流的分尺度能量时，能量更加集中于低频(高模态)部分，更有利于大尺度相干结构的提取．

笔者首先对实验数据进行概率密度统计，并与高斯分布比较，验证了由相干结构引起的猝发现象的统计规律．然后将湍流脉动速度进行 HHT变换分析，将大尺度(高模态)相干结构提取出来．应用小波变换中小波系数重构的方法继续处理剩余信号，将小尺度相干结构提取出来．最后将提取出的全部相干结构信号与对应壁面距离处的壁湍流脉动速度进行相关分析并进行比较．

1 实验装置与测量方法

实验在直流抽吸式低(变)湍流度的闭口风洞中进行，在该风洞实验段中放置一块长 4.5,m，宽0.35,m，厚 5,mm，前缘为楔形的平板．平板上游粘贴砂纸以加速转捩，在距平板前缘 2.4,m的实验测量位置处放置一根标定好的热线探针，探针由三维坐标架固定并与恒温热线风速仪IFA-300相连接，采集的数据由计算机进行处理．实验装置如图1所示．

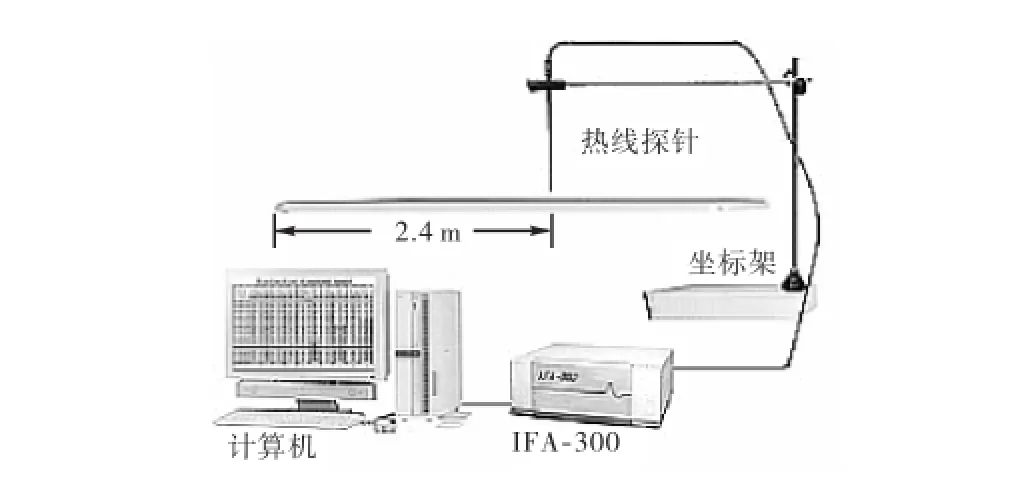
图1 实验装置Fig.1 Experimental setup

对风洞内壁湍流脉动速度进行测量时，热线探针的初始位置(见图 1)为距平板前缘 2.4,m处，位于平板上方 0.3,mm的高度，考虑到边界层流场的特点，以不同的增长间距共设置了84个不同法向位置的测量点．将测得的数据文件应用 Matlab编程处理，进行相关湍流分析．

2 实验数据分析

采用概率统计方法分析脉动速度分布特征与壁湍流猝发的关系；利用 HHT和小波重构法提取含能的全尺度壁湍流相干结构，并分析其时频分布特性．

2.1 脉动速度的统计特性分析

将实验测量的湍流脉动速度做概率统计分析，取2个不同的壁面距离y+=10.0和y+=610.3，分别做概率密度分布(PDF)曲线，将其归一化后与标准高斯曲线进行比较，如图2所示．

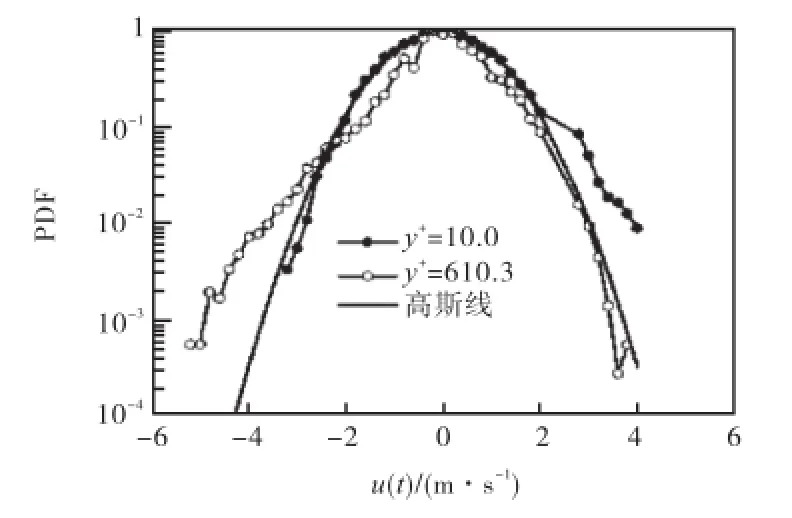
图2 湍流信号概率密度曲线与标准高斯线的比较Fig.2 Comparison of turbulent probability density curve with standard Gaussian line

从图2中可以看出，在近壁区域y+=10.0处概率密度曲线较高斯线正偏，而在较远壁区域 y+=610.3处概率密度曲线较高斯线负偏．流向脉动速度的这种分布特征与壁面附近湍流猝发的扫掠和喷发事件有关．远壁区脉动速度主要受低速流体喷发事件的影响，因而流向脉动速度分布负偏；而在壁面附近区域，脉动速度主要受制于高速流体的扫掠运动，因而流向脉动速度概率分布正偏．这是由湍流边界层中有组织的相干结构运动引起的典型现象．

湍流随机变量的分布特征还常用偏斜度(skewness)来描述．偏斜度用 S表示，表征随机变量概率密度函数的对称性，即S=0表示概率密度函数f关于均值中心对称；若 S＜0，则概率密度函数左偏或负偏；若S＞0，则概率密度函数右偏或正偏．

为了更深入地了解实验测量数据的统计特性，研究了偏斜因子随壁面距离的变化规律，如图 3所示．容易看出，在壁面距离由小变大的过程中，偏斜因子的值由正值变为负值．这与图 2近壁区脉动速度概率密度曲线由正偏过渡为远壁的负偏相一致，说明近壁扫掠事件占优势，虽然从局部扫掠阶段的后期到局部猝发的开始之间时间很短，但是大部分雷诺应力是在这段时间产生的；而到了远壁，低速流体向后上方喷射进入边界层外层区域，这导致反流向的脉动速度成分增加，流向脉动速度被削弱．猝发现象说明湍流脉动不是随机过程，湍流脉动信号中存在具有一定内在规律的拟序结构，亦即相干结构．

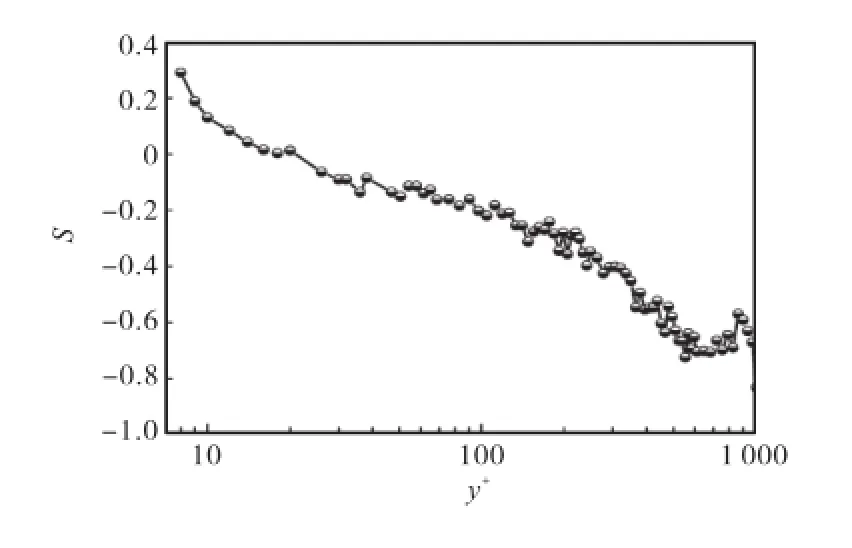
图3 由近壁到远壁偏斜因子的变化曲线Fig.3 Variation of skew factor with wall distance

2.2 应用HHT方法提取大尺度相干结构

1998年，黄锷提出了经验模态分解方法，Huang等认为，实际信号基本上都是多成分信号，即同一时刻信号包含多种频率成分，某一时刻对应的瞬时频率没有明显的物理意义．该方法将湍流信号进行平稳化处理，对信号中不同尺度的波动或趋势项逐级分解开来，产生一系列不同特征尺度的数据序列，每个序列称为一个固有模态函数(IMF)分量．对分解得到的分量进行 Hilbert变换得到信号在频域或时域上的分布规律．为了使得瞬时频率具有明显的物理意义，Huang等[10]在原有特征尺度分解的基础上，提出了内模函数的概念和经验模态分解方法．Huang用内模函数来近似单一成分信号，并做出如下定义：

(1) 极值点的个数和过零点的数目相等，或者最多相差1；

(2) 在任一点，由极大值构成的包络和由极小值构成的包络的平均值为零．

其中条件(1)将信号限制为窄带信号，条件(2)可以保证求得的 IMF瞬时频率有意义．这2个条件保证了后续 Hilbert变换的可行性．凡满足以上2个条件的分量就看作是一个内模函数．为了从原始数据中分解出内模函数，Huang也给出了具体的经验模态分解方法[10]．

应用该方法将湍流脉动速度信号做 Huang变换分解成多个模态，再做Hilbert变换，求得不同壁面距离下各模态的能量变化．需要说明的是 Hilbert-Huang变换过程中，由于内模函数由极值包络的对称性来判定，第一模态对应的分量包络波动性最大，相应频率范围也最大．模态越高对应的频率范围越窄，值也越小，即高模态对应低频率段，低模态对应高频率段．本文选取 4个不同壁面距离的湍流脉动速度，分别为y+=8.0、y+=30.0、y+=61.4和y+=162.5．图4所示为HHT分解各模态能量变化分布曲线．

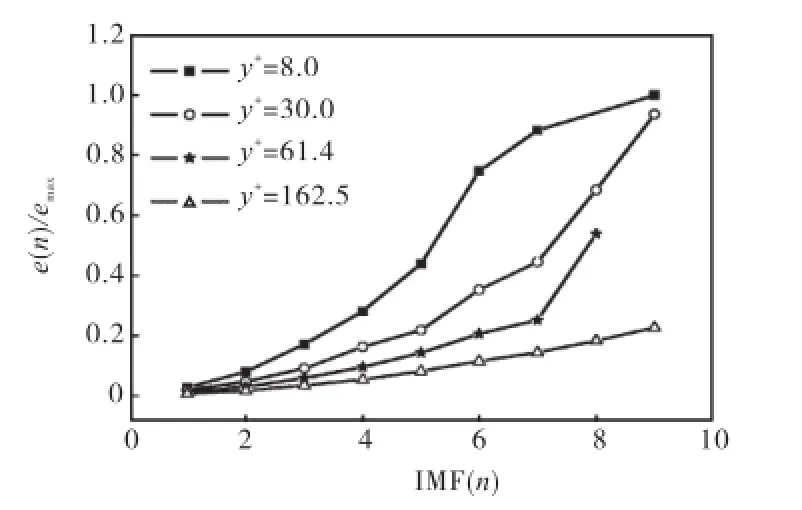
图4 HHT分解模态的能量变化分布曲线Fig.4 Modal energy of HHT

图 4中，横轴为 HHT分解的模态，纵轴为各模态能量的归一化结果．可以看出，高模态(低频)部分含能较高，这首先与湍流脉动信号本身有关，因为低频率部分代表着大尺度湍涡结构，而大尺度涡结构构成相干结构的主要部分，含能也最高．其次，流场的不稳定性和剪切作用，使来自平均流场的湍能沿低频(高模态)部分逐级向高频(低模态)部分传递[11]，湍能依靠湍涡之间的相互作用进行传输，同时该传输过程存在着反向能量级串[9]，这使得湍能在传递过程中逐级减少，呈现在图中则表现为随着模态的增加，能量也逐级增加．再次，HHT分解方法以 IMF当作展开的基底，分解完全基于信号本身的性质．将IMF分量作 Hilbert变换对应的模态能量更能代表真实频段湍流信号的能量．研究表明，HHT分解信号时，能量更加集中于低频部分[8，12]，因此 HHT分解更适合提取大尺度的相干结构．

统计主要含能的大尺度低频模态，这些高能量模态所含能量占该壁面距离处湍流信号总能量的比例如表1所示．

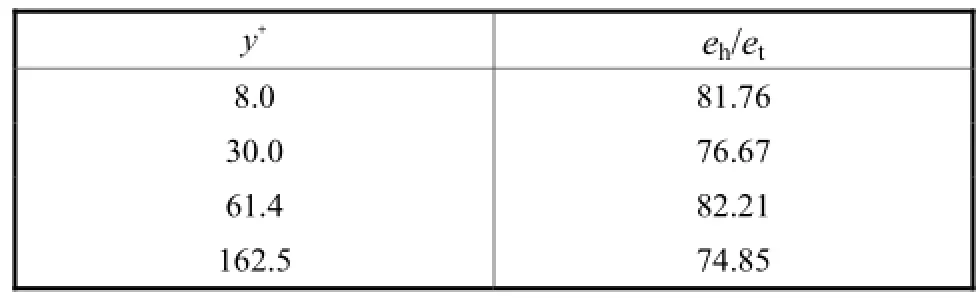
表1 高模态能量eh占总能量et百分比Tab.1 Percentage of high modal energy share the total energy %

由表 1看出，高模态能量所占总能量比例可达到 80%左右，占总能量的绝大部分．分析高含能模态并将其与传统方法提取出的相干结构进行比较，结果表明上述高含能模态与相干结构的特性近似相同，是相干结构的主要部分．基于上述结论，将高模态的IMF分量从原信号中分离出来，将剩余模态分量进行重构．重构后的剩余信号已去除主要含能的湍流相干结构，为近似随机的湍流信号．分析重构后剩余信号的概率密度分布曲线，并与标准高斯曲线进行比较．图 5所示为 y+=30.0壁面距离处剩余信号的概率密度分布与标准高斯分布的比较．

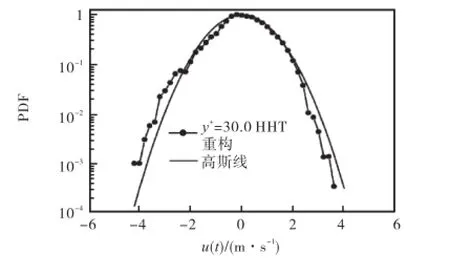
图5 重构信号概率密度曲线与高斯线比较Fig.5 Comparison of the probability density curve reconstructed with the Gaussian line

由表1可知，y+=30.0处分离出的大尺度相干结构能量占总能量的 76.67%，剩余信号能量仅占总能量的23.33%．从图5中可以看出，重构后的剩余信号概率密度曲线与标准高斯曲线相比，略微存在一些差别．原因在于相干结构分布于湍流信号的整个频段内，由于 HHT分解具有“低频能量集中”特性，利用 HHT将高模态 IMF分量分离是将主要含能的大尺度(低频段)湍涡结构去除，而对于全部相干结构包含的小尺度(高频段)部分相干结构，HHT方法未对其进行提取．

2.3 小波变换提取小尺度间歇事件

相干结构具有多尺度分布特征，不仅存在于大尺度结构中，也存在于小尺度结构中[7]，其中大尺度(低频率)部分中的相干结构已在第 2.2节中采用 HHT方法从原始信号中分离出来，剩余的非随机成分为小尺度相干结构，这部分相干结构表现为可由间歇因子表征的含能较多的强间歇结构．所谓间歇因子是根据小波系数引入的表征间歇性的量化指标，其计算公式为

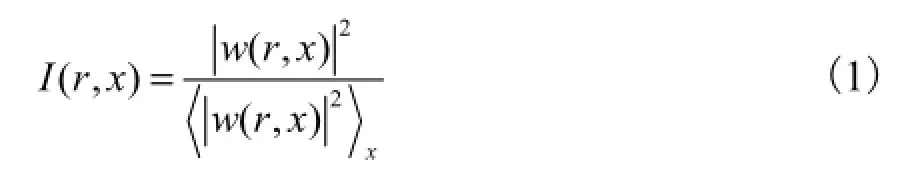
式中：I(r，x)为小波分析中各尺度的局部间歇强度；w(r，x)为不同壁面距离、不同尺度下的小波系数；r为壁面距离；x为尺度．

将第 2.2节中的重构信号采用小波变换进行多尺度分解．为了减少能量泄露，对比多个小波函数，最后选用“db20”作为小波基函数，使能量泄露最少．由于小尺度相干结构含有更多的能量，分析实验数据的统计结果，选取小波分解后各尺度小波系数间歇因子的均值作为判定强间歇事件的门限值 L，其计算公式为

式中：I(r，x(i))为同一壁面距离同一尺度下的各小波系数对应的间歇因子；L(x)为第x尺度下由该尺度n个间歇因子决定的门限值．

对强间歇事件以外的各尺度小波系数均设为零，然后经过小波重构后可以提取出具有强间歇性的小尺度相干结构．同样地，将强间歇事件对应的各尺度小波系数置为零，各尺度小波系数信号重构得到去除相干结构之后的剩余信号．图6所示为y+=30.0时，剩余信号的概率密度分布曲线与标准高斯曲线进行比较，2条曲线已非常接近，表明经过HHT以及小波变换处理后，已将绝大部分湍流相干结构提取出来，剩余部分为近似高斯型的带有随机特征的湍流信号．比较图2和图5，可以看出经过HHT后，已经将大部分含能最多的大尺度相干结构从原湍流信号中分离出来，但仍留存有部分小尺度湍流信号．而原始湍流信号u(t)可表示为

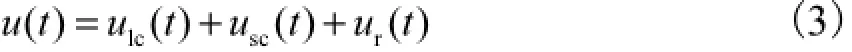
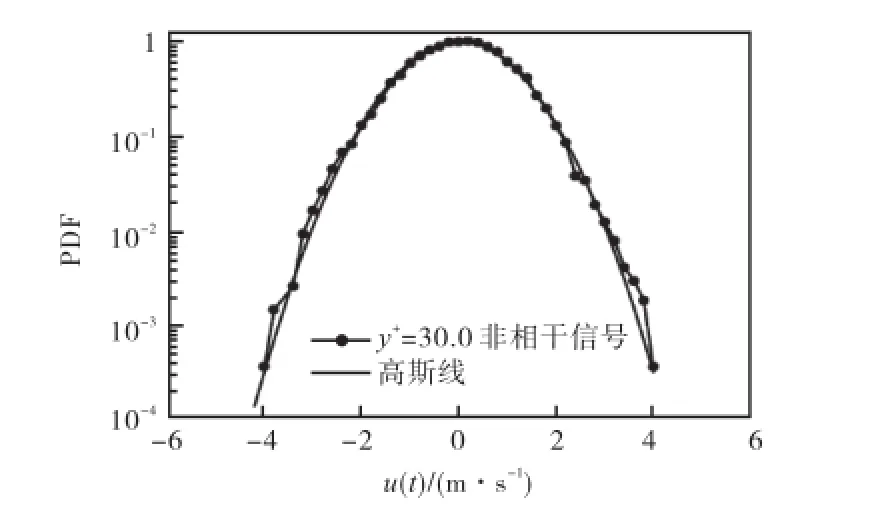
图6 小波处理后概率密度曲线与高斯线比较Fig.6 Comparison of probability density curve continuely treated by wavelet with the Gaussian line

式中：ulc(t)为大尺度湍流信号，该部分已由 HHT方法提取出来；usc(t)为小尺度间歇事件湍流信号，该部分由小波系数重构的方法提取完成；ur(t)为非相干湍流成分，即为图6中的剩余信号．度(高频)部分的相干结构后，经小波系数重构获得的湍流脉动速度的概率密度分布曲线与标准高斯曲线基本吻合，说明在经过小波变换对小尺度强间歇事件进行提取后，剩余的湍流接近随机信号，因此壁湍流相干结构与原始湍流信号完全分离．

2.4 提取的相干结构与原始湍流信号的比较

为了进一步研究提取出的相干结构的性质，将采用HHT方法提取出的大尺度相干结构信号与提取出的小尺度相干结构引起的间歇事件信号叠加，以y+= 30.0为例，获得湍流脉动信号中全部相干结构的信号(见图7)，并与原始湍流信号(图8)比较．

对比图7和图8可以看出，提取前后脉动较强部分分布的时间比较一致，只是脉动速度的大小有一定差别，原始湍流脉动速度较大，这是由于湍流信号除了包含相干结构外还包含有随机的非相干成分．

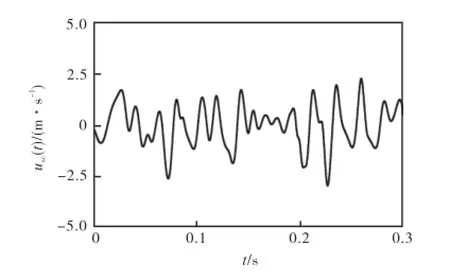
图7 提取的相干结构信号(y+=30.0)Fig.7 Extracted coherent structure(y+=30.0)

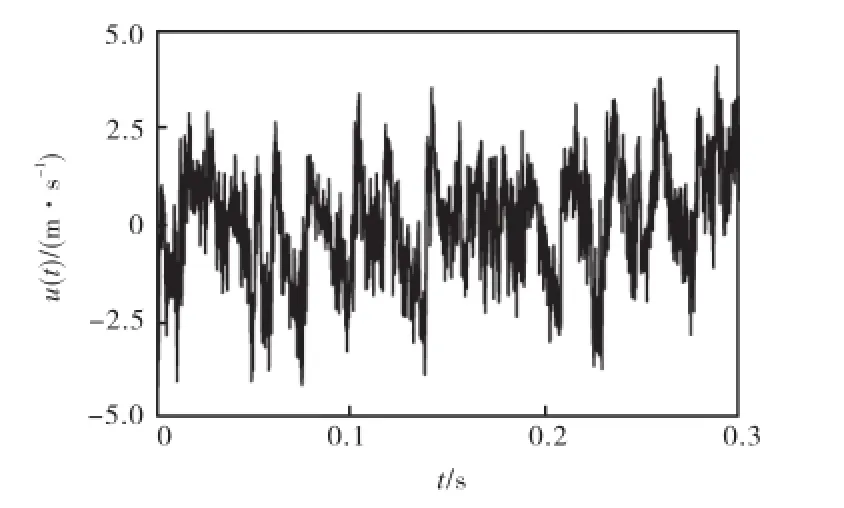
图8 原始湍流信号(y+=30.0)Fig.8 Original turbulent signal(y+=30.0)

分析相干结构信号的 HHT边际谱，并与原始湍流脉动速度信号的 HHT边际谱进行比较．所谓边际谱是从统计意义上表征整组数据每个频率点的累积幅值分布．用于处理湍流这样的瞬态信号时，如果信号中出现某一频率的能量，就表示一定存在该频率的振动波，故边际谱可以更准确地反映湍流信号的实际频率成分，更适合湍流信号的分析．图9所示为y+= 30.0处提取出的相干结构HHT边际谱和原始湍流脉动速度HHT边际谱的比较．

图9中，横轴为频率，纵轴为对应频域下信号能量(Abs.,magnitude)的归一化值．可以看出，较低频率(大尺度)部分提取相干结构前后的2条曲线基本重合；较高频率(小尺度)部分提取相干结构后曲线快速衰减，说明主要含能的大尺度相干结构集中于低频部分，而高频部分含有较多非相干信号，这与Farge等[13]应用数值模拟方法提取相干结构获得频谱图的趋势相同．

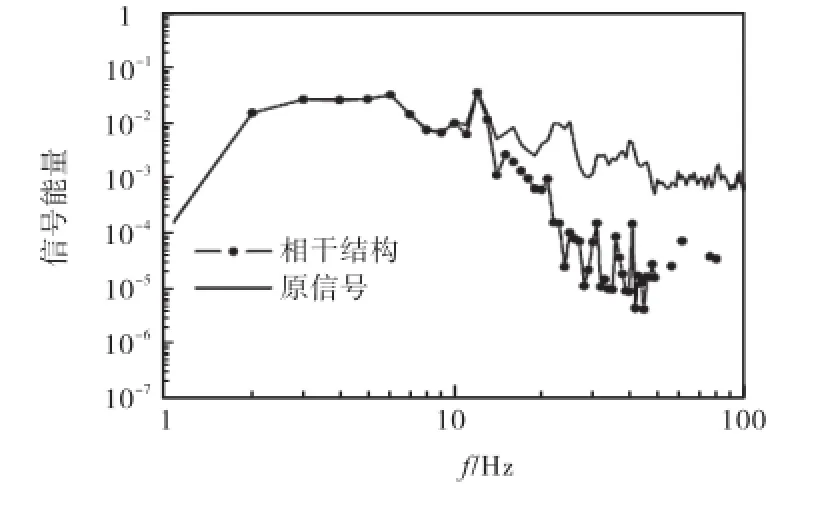
图9 相干结构与原信号的边际谱比较(y+=30.0)Fig.9 Comparison of HHT marginal spectrum between coherent structure and the original signal (y+=30.0)

3 结论

(1) 近壁区脉动速度概率密度曲线向正方向偏离高斯曲线，在稍远壁区正好相反，说明由相干结构引起的典型“猝发”现象导致湍流脉动速度分布具有分层特征．

(2) 基于 HHT方法本身的优点，其对低频部分的相干结构提取更准确．且该提取部分能量约占湍流信号总能量的 80%．用小波变换中小波系数重构方法将剩余信号中的强间歇事件进行提取．最后剩余信号的概率密度分布曲线与标准高斯曲线吻合较好，相干结构得到了较完全的提取．

(3) 提取出的全部相干结构数据与原始湍流脉动速度比较，验证了湍流信号既包含非随机的相干结构信号也包含随机的非相干信号．将相干结构数据的 HHT边际谱与原始湍流信号 HHT边际谱比较，在较低频率部分提取相干结构前后的 2条曲线基本重合，而对于较高频率部分提取相干结构后曲线快速衰减，2条曲线逐渐分离．

［1］ Brodkey R S，Wallace J M，Eckelmann H. Some properties of truncated turbulence signals in bounded shear flows[J]. Journal of Fluid Mechanics，1974，63(2)：209-224.

［2］ Kim J，Moin P，Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number[J]. Journal of Fluid Mechanics，1987，177：133-166.

［3］ Moin P，Kim J. Numerical investigation of turbulent channel flow [J]. Journal of Fluid Mechanics，1982，118：341-377.

［4］周济福，张强，李家春. 近壁湍流脉动的概率分布函数[J]. 应用数学和力学，2005，26(10)：1135-1143.

Zhou Jifu，Zhang Qiang，Li Jiachun. Probability distribution function of near-wall turbulent velocity fluctuations [J]. Applied Mathematics and Mechanics，2005，26(10)：1135-1143(in Chinese).

［5］ Douady S，Couder Y，Brachet M E. Direct observation of the intermittency of intense vorticity filaments in turbulence[J]. Physics Review Letters，1991，67(8)：983-986.

［6］ She Z S，Jackson E，Orszag S A. Intermittent vortex structures in homogeneous isotropic turbulence[J]. Nature，1990，344(15)：226-228.

［7］姜楠，柴雅彬. 用子波系数概率密度函数研究湍流多尺度结构的间歇性[J]. 航空动力学报，2005，20(5)：718-724.

Jiang Nan，Chai Yabin. Experimental investigation of multi-scale eddy structures′ intermittency in turbulent flow using probability density function of wavelet coefficients[J]. Journal of Aerospace Power，2005，20(5)：718-724(in Chinese).

［8］黄永祥. 圆柱绕流和大气湍流的Hilbert-Huang变换分析[D]. 上海：上海大学力学所，2006.

Huang Yongxiang. Circular Cylinder and Atmospheric Turbulence Analyzed by Hilbert-Huang Transform[D]. Shanghai： Institute of mechanics， Shanghai University，2006(in Chinese).

［9］ Xia Zhenyan，Tian Yan，Jiang Nan. Wavelet spectrum analysis on energy transfer of multi-scale structures in wall turbulence[J]. Applied Mathematics and Mechanics：English Edition，2009，30(4)：435-443.

［10］ Huang N E，Long S R，Shan Z. The mechanism for frequency downshift in nonlinear wave evolution[J]. Advances in Applied Mechanics，1996，32：59-117.

［11］ Xia Zhenyan，Jiang Nan，Tian Yan，et al. Experimental study on the local similarity scaling of the turbulence spectrum in the turbulent boundary layer[J]. Science in China Series：Physics，Mechanics & Astronomy，2009，39(3)：428-434.

［12］连海宁. 傅里叶、小波及希尔波特-黄变换在地震工程领域的应用研究[D]. 北京：中国地震局工程力学研究所，2004.

Lian Haining. Fourier，Wavelet and Hilbert-Huang Transform Applied in the Field of Earthquake Engineering Research[D]. Beijing：Institute of Engineering Mechanics of China Earthquake Administration，2004(in Chinese).

［13］ Farge M，Schneider K，Pellegrino G，et al. Coherent vortex extraction in three-dimensional homogeneous turbulence：Comparison between CVS-wavelet and PODFourier decompositions[J]. Physics of Fluids，2003，15(10)：2886-2896.

Extraction of Coherent Structures in Wall Turbulence Based on Wavelet and Hilbert-Huang Transforms

XIA Zhen-yan1,2，JIN Xiu-qing1,2，JIANG Nan1,2
(1. Department of Mechanics，Tianjin University，Tianjin 300072，China；2. Tianjin Key Laboratory of Modern Engineering Mechanics，Tianjin 300072，China)

In order to study the coherent structures in wall turbulence，the constant temperature hot-wire anemometer IFA-300 was used to measure the flow velocity signals at different normal locations of the turbulent boundary layer in the wind tunnel，which is of direct suction-type low(variable)turbulent intensity. The probability density distribution of wall turbulence fluctuating velocity was analyzed and compared with the Gaussian curves，and the results confirm the statistical laws of bursts caused by coherent structures in wall turbulence. A method for extracting coherent structures was proposed，which is hybridized by wavelet transform and Hilbert-Huang transform(HHT). The HHT was applied to analyze the turbulent fluctuation velocity，and the main coherent structures were extracted by analyzing the energy of each mode. The wavelet reconstruction method was used to extract small-scale coherent structures from the left data. The probability density distribution of the remained signals was analyzed. All of the coherent structures extracted by the above method were compared with the original turbulent signal，and their HHT marginal spectrums were also compared，which verifies that turbulence signal contains both non-random coherent signal and random noncoherent signal.

Hilbert-Huang transform；wavelet transform；wall turbulence；coherent structures；intermittency