非规则部分校准阵列下的宽带LFM信号二维DOA估计

罗 蓬，刘开华，史伟光，闫 格

(天津大学电子信息工程学院，天津 300072)

非规则部分校准阵列下的宽带LFM信号二维DOA估计

罗 蓬，刘开华，史伟光，闫 格

(天津大学电子信息工程学院，天津 300072)

提出了一种宽带线性调频(LFM)信号的二维波达方向(DOA)估计新方法．该方法在空域和时域同时对信号进行采样，并利用观测样本的分数阶Fourier域峰值构造出新的时频空DOA矩阵，进而通过特征值分解的方法实现多个LFM信号的DOA估计．该方法充分地挖掘了观测信号所包含的时频信息，降低了对阵列结构和阵元一致性的约束，使其适用于阵元几何分布不规则且大部分阵元未经校准的阵列．此外，该方法无需谱峰搜索和二维参数配对，计算简单且估计精度较高．仿真结果显示，在DOA估计的均方根误差(RMSE)相同时，与传统方法相比，该方法可获得6～8 dB的信噪比增益．

阵列信号处理；二维DOA估计；FrFT；宽带LFM信号；部分校准阵列

线性调频(linear frequency modulation，LFM)信号广泛地应用于雷达、声纳和通信等信息系统中[1-3].在这些系统中，LFM 信号的波达方向(direction of arrival，DOA)估计是一个重要的研究课题．由于LFM 信号具有宽带非平稳的特性，其阵列方向矩阵与时间相关，因此常规的子空间算法不再适用于这类信号的 DOA估计．近年来，将信号的时频特征和空域信息相结合的时频空算法成为该领域一个研究热点．沿着这个方向已经出现了一些研究成果[4-6]，其中以国内学者陶然、齐林等提出的基于分数阶Fourier变换(fractional Fourier transform，FrFT)的LFM信号DOA估计方法[7-9]最受关注．由于FrFT是一种线性变换，不受交叉项的干扰，而且可以理解为LFM基分解，所以在对LFM信号的处理上比其他时频变换方法更有优势．

现有的LFM信号DOA估计方法都是针对各种规则阵列结构提出的，而且假设阵列具有理想的阵列流形(或阵列已被校准)．然而，在实际应用中，由于设备的内部空间、载体、工作环境等因素的限制，阵列的几何结构往往是不规则的．另外，阵元实际位置和标称位置之间存在的偏差、各阵元幅度和相位特性的不一致等因素都会使阵列流形产生误差，导致传统方法估计性能的急剧下降．

针对上述问题，笔者提出了一种基于FrFT的宽带 LFM信号二维DOA估计新方法．该方法在空域和时域同时对入射信号进行采样，并利用观测样本的FrFT峰值构造出新的时频空DOA矩阵，进而通过特征值分解的方法实现各LFM信号的DOA估计．该方法充分地挖掘了观测信号所包含的时频信息，降低了对阵列结构和阵元一致性的约束，使其适用于阵元几何分布不规则且大部分阵元未经校准的阵列．此外，该方法无需谱峰搜索和二维参数配对，计算简单且估计精度较高，适合工程应用．最后给出了该方法的实施步骤，并通过仿真实验验证了其有效性．

1 阵列结构与信号模型

假设阵列由M个任意分布的全向阵元构成，如图1所示．令第1个阵元为参考阵元，并将其位置设为坐标原点．远场处有K个宽带LFM信号入射到该阵列上，其中第k个信号的表达式为

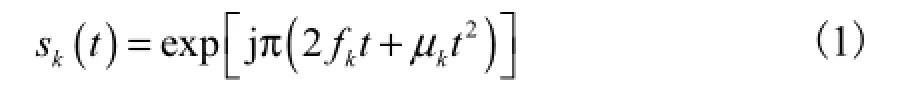
式中fk和 μk分别表示该信号的中心频率和调频率参数．

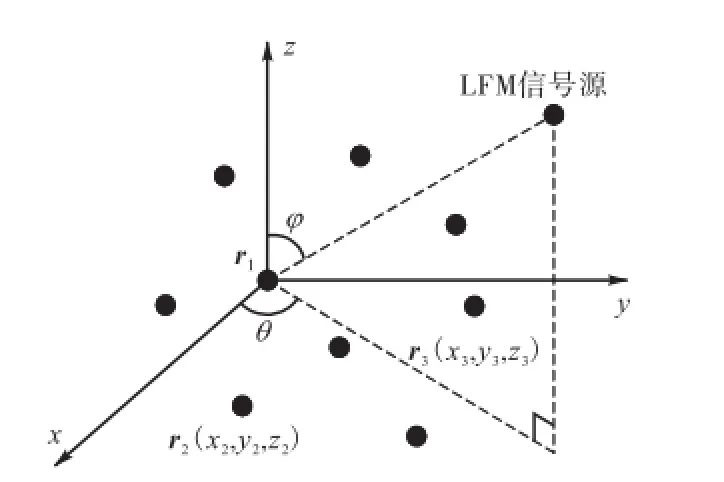
图1 非规则阵列结构示意Fig.1 Irregular geometry array

对入射信号进行空域与时域联合采样，空域样本由M个阵元的输出得到，时域样本由阵元上的N个延时抽头的输出得到，则第 m个阵元上的第 n个延时抽头的输出信号为

式中：gm为第 m个阵元的复增益(幅相误差)；nm(t)为第 m个阵元上的零均值高斯白噪声，这里假设各入射信号之间、各阵元上的噪声之间以及信号和噪声之间均不相关；Ts为时域采样间隔；τmk为第 k个LFM信号到达第m个阵元时相对于参考阵元的传播延时，即

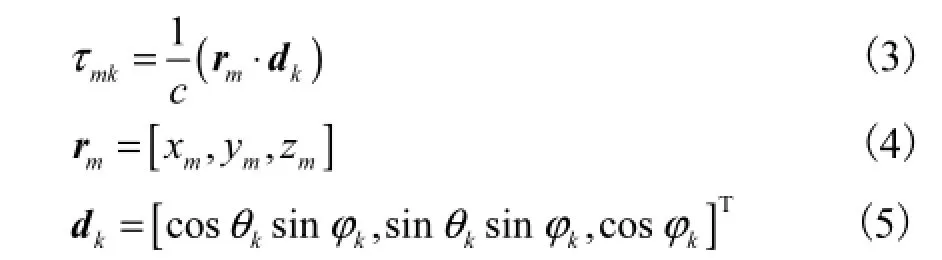
式中：rm为第 m个阵元的位置矢量；θk和 φk分别为第k个入射信号的方位角和俯仰角．

选择不在同一直线上的3个阵元为引导阵元，不失一般性，假设它们位于xy平面上，有

并假设这3个阵元为已校准阵元，不失一般性，令

需要注意的是，这里假设除 3个引导阵元外，其余阵元均为非校准的，即gm与rm(4≤m≤M)均未知．

2 提出的LFM信号二维DOA估计方法

2.1 阵列信号的分数阶Fourier变换

一个信号x(t)的旋转角度为α的FrFT定义为

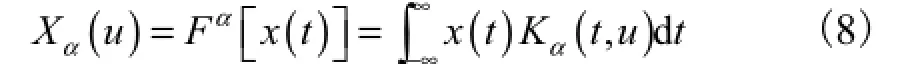
其中Kα(t，u)为变换核函数，有

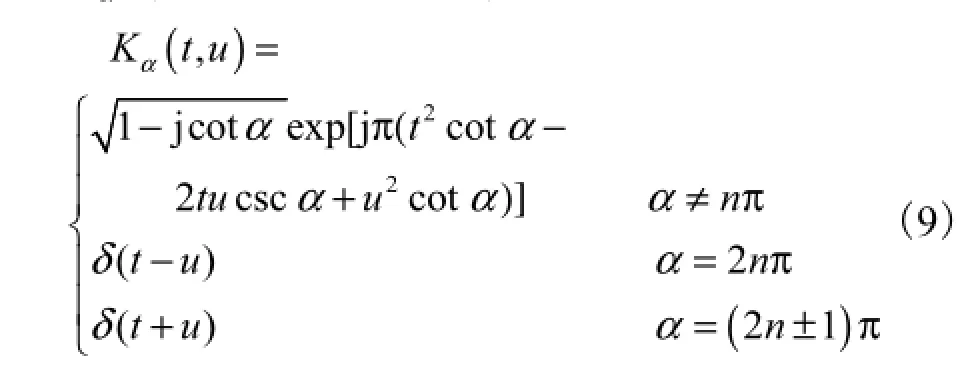
对于第k个入射LFM信号，有

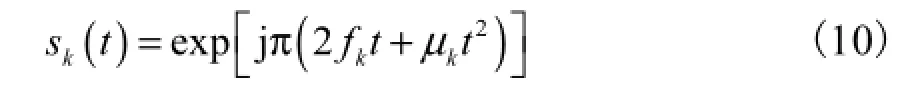
令其FrFT为

则 Sk(α，u)在(α，u)平面上将形成一个能量聚集的谱峰[10]，且谱峰位置和谱峰值分别为

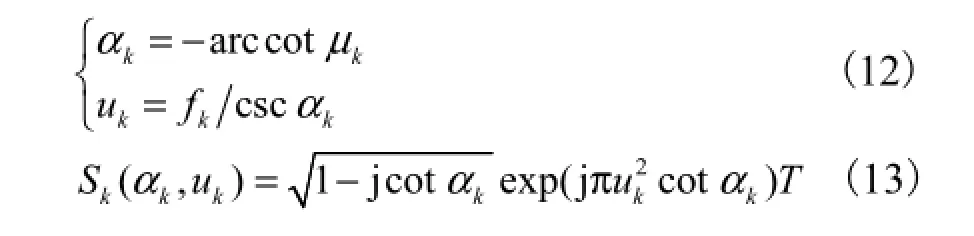
式中T为信号的观测时间长度．

由式(1)和式(2)可知，sk(t)在第 m个阵元上的输出为

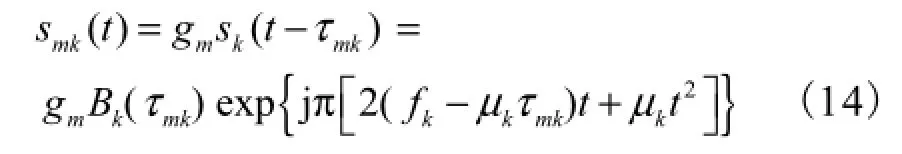
其中

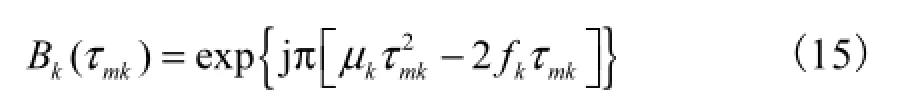
为一个只与延时有关的常数．由于 LFM 信号经过延时后调频率保持不变，令smk(t)的FrFT为Smk(α，u)，则Smk(α，u)的谱峰位置和谱峰值分别为

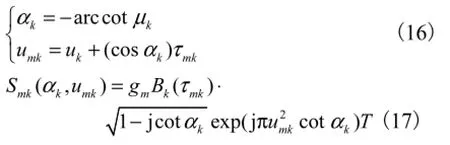
对比式(13)和式(17)，可以得到

式(18)反映了 LFM 信号经过延时后在分数阶Fourier域的峰值变化情况，其中

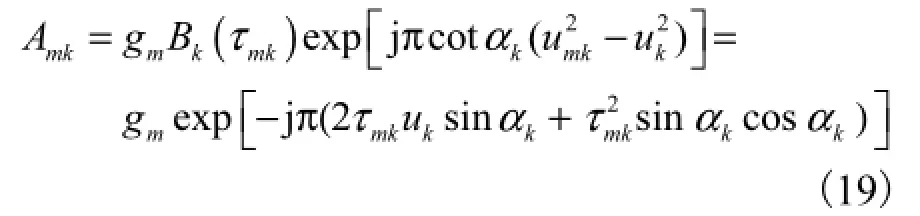
考虑到阵元延时 τmk的二次项很小，在实际应用中可以忽略，因此上式可以简写为

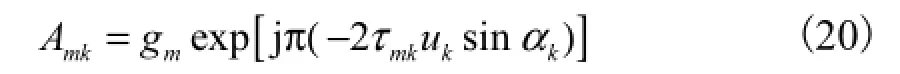
2.2 非规则部分校准阵列下的二维DOA估计

由第2.1节的分析可知，不同的阵元接收到同一个 LFM 信号后，各阵元的输出会在相同的分数阶Fourier域上达到能量聚集，而阵元之间的延时则会影响谱峰出现的位置和峰值大小．由于 FrFT是一种线性变换，根据其可加性可知，K个 LFM 信号在阵元上的叠加会在K个不同的分数阶Fourier域上出现峰值，因此通过选取不同的峰值点数据即可实现各LFM 信号的分离，从而简化数据模型．对式(2)的两端进行FrFT可以得到

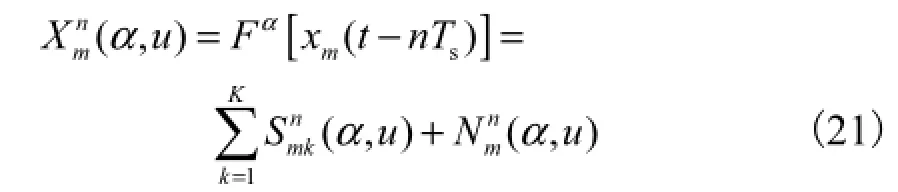
其中

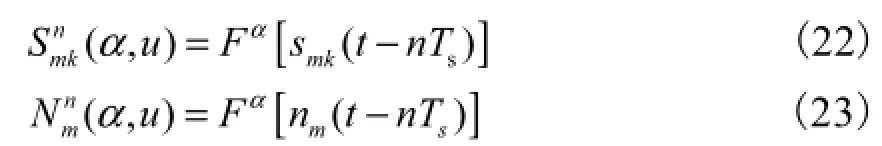
由于不同的入射信号具有不同的时频特性，在第k个LFM信号对应的峰值点处，其他信号均未达到能量聚集，取值可以忽略，即

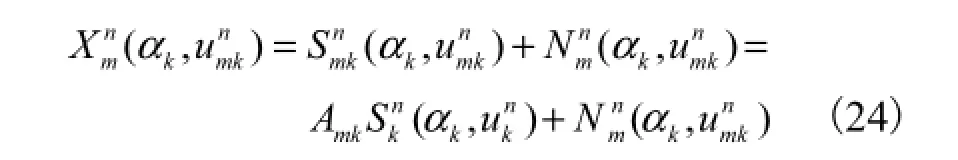
为了估计第k个LFM信号的二维DOA参数，选择该信号对应的分数阶Fourier域峰值点数据作为阵元上的观测数据，并定义参考阵元与各阵元的时频输出的互相关函数为

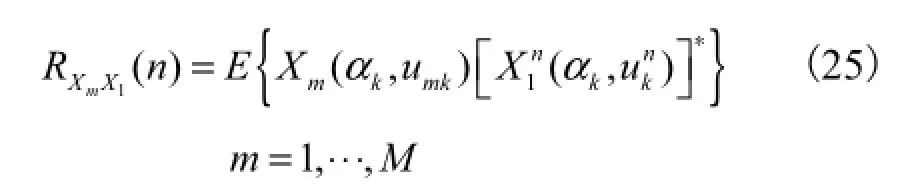
由于 FrFT不改变高斯白噪声的统计特性[11]，因此式(25)可以化简为

当拉张伸展的方向与前一地质历史时期的挤压方向近于相反时，基底中的逆冲体系易发生应力集中，从而发生负反转作用。在负反转作用过程中，逆冲断层能否重新活动取决于两个主要因素：一是断层倾角，角度大的较难活动，角度小的较易活动；二是后期叠加的应力场方向，应力方向垂直于断层走向的容易，其他方向的较难。前期逆冲上升，上盘地层遭到严重剥蚀，下盘地层保存完整；后期上盘下滑，表现为同期沉积断层的特征。

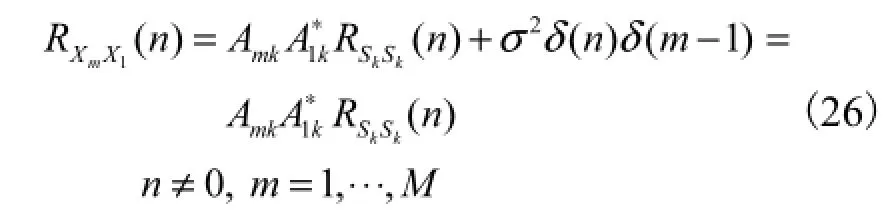
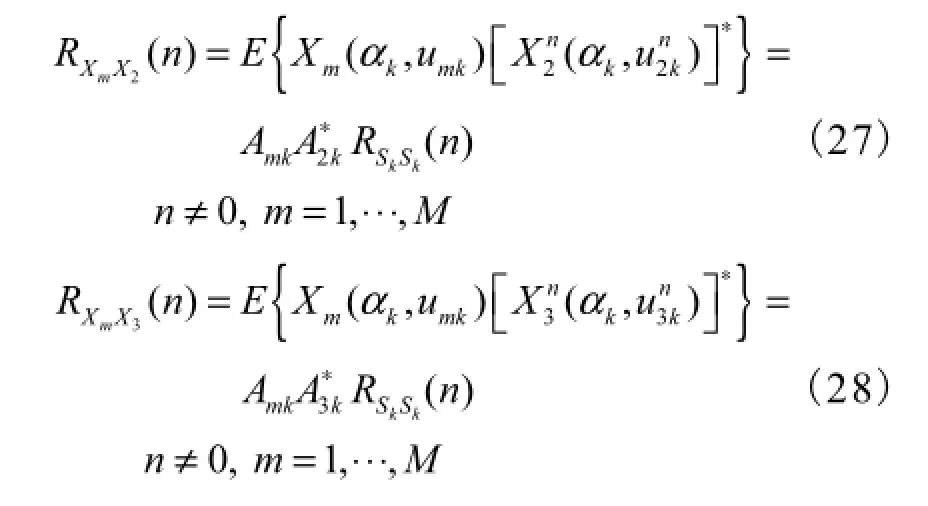
对式(26)～式(28)进行空时联合采样，即当 m由 1变到M、n由1变到N时，可以形成相关矩阵

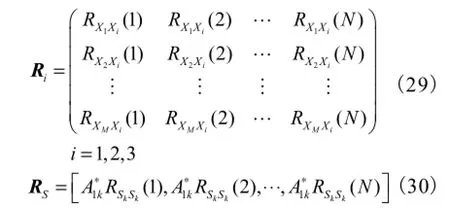
则式(26)～式(28)的矩阵形式可以分别表示为

式中：Ak为第 k个LFM信号的分数阶Fourier域方向向量，Ak=[A1k，A2k，…，AMk]T；Φ1和Φ2分别满足

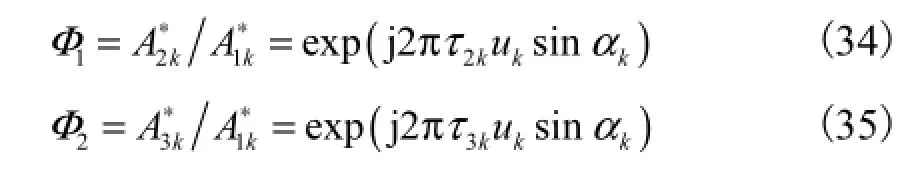
定义时频空DOA矩阵

根据文献[12]的结论，矩阵X和Y的非零特征值分别等于Φ1和Φ2，而且特征值对应的特征向量等于信号的方向向量Ak，即

因此，分别对X和Y进行特征值分解，即可得到Φ1、Φ2以及 Ak的估计．由式(3)～式(6)以及式(34)、式(35)可得

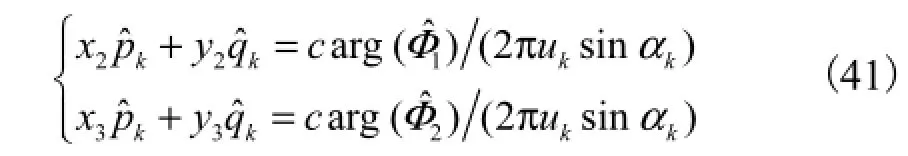
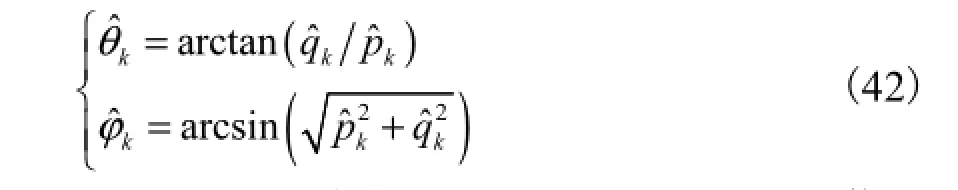
需要指出的是，该方法利用了不同的 LFM 信号在不同的分数阶 Fourier域上达到能量聚集这一特点，通过不断改变 FrFT的阶次实现各入射 LFM信号的分离，然后逐一估计出它们的二维 DOA参数，因此该方法无需额外的二维参数配对过程，减少了计算量．此外，该方法不仅能够估计出入射信号的DOA参数，还可以得到各入射信号的阵列响应矩阵Ak(k=1，2，…，K)，该矩阵在阵列校正等应用中具有重要的作用．

2.3 有色噪声情况

上述分析均假设阵元上的噪声为白噪声，然而在实际应用中，通道输出中的噪声经常是有色噪声．针对这一情况，对所提方法进行如下修正．

假设不同阵元间的噪声互不相关，即

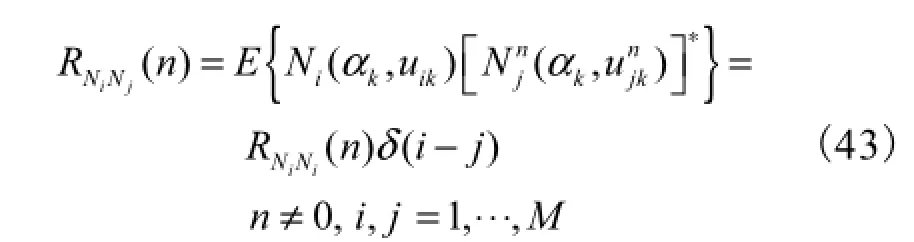
利用阵元间的不相关性，将式(26)修正为

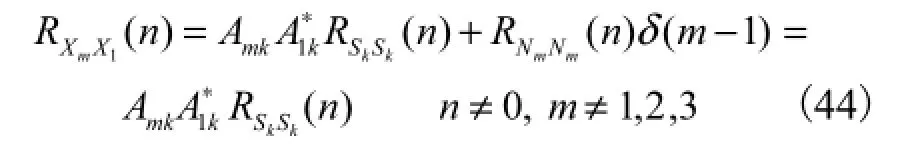
同理，式(27)和式(28)也可修正为

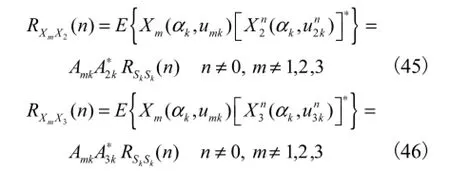
因此同样有式(31)～式(33)成立，接下来仍可采用所提方法实现DOA以及阵列响应的估计．需要注意的是，此时向量Ak和RS需要在前述形式的基础上做相应的抽取，导致阵列的有效孔径略有下降．

2.4 算法的实施步骤

总结以上的分析，将算法的主要步骤归纳如下：

(1) 对参考阵元上的观测信号进行连续变化阶次的 FrFT，并对(α，u)平面做二维搜索，通过谱峰个数估计出入射 LFM 信号的个数，并记录各入射信号对应的谱峰位置(αk，uk)；

(2) 对各个阵元以及阵元上的延时抽头的输出信号进行角度为αk的FrFT并做一维搜索，得到相应的峰值点数据作为该阵元的时频输出；

(3) 构造式(29)所示的相关矩阵R1、R2以及R3，并按照式(36)和式(37)计算时频空DOA矩阵X和Y；

(4) 分别对X和Y进行特征值分解，通过非零特征值以及对应的特征向量估计Φ1、Φ2以及Ak的值，进而按照式(41)和式(42)估计出第k个LFM信号的方位角与俯仰角；

(5) 重复步骤(2)～(4)，直至估计出所有入射信号的二维DOA参数．

另外，在上述谱峰搜索过程中采用“粗扫描+细扫描”的二阶搜索方法，可以大大减少算法的运算复杂度．

3 仿真实验

3.1 本文方法的估计性能分析实验

构造一个8阵元的非规则立体阵，并选取3个不在同一直线上的阵元作为引导阵元．除引导阵元外，随机选取其余阵元的复增益 gm．3个相互独立的等幅宽带 LFM 信号分别以入射角(60°，25°)、(45°，55°)、(30°，70°)入射到阵列上，信号的初始参数分别设置为：f1=20,MHz，μ1=-0.066,MHz/µs，f2= -10,MHz，μ2=0.08,MHz/µs，f3=10,MHz，μ3= 0.015,MHz/µs．采样频率为100,MHz，快拍数为501，引导阵元上的延时抽头个数为20，阵元噪声为10 dB的高斯白噪声．图2为参考阵元上观测信号的连续变化阶次FrFT的二维扫描谱．

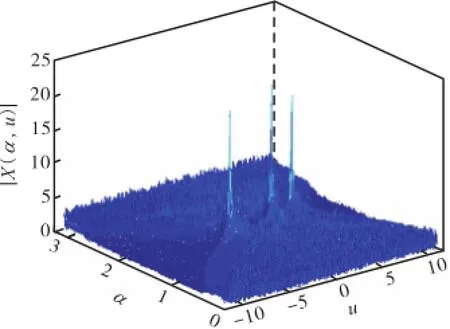
图2 入射信号的二维FrFT扫描谱Fig.2 2-D FrFT scan spectrum of incident signals

从图2中可以看出，在(α，u)平面上存在3个明显的谱峰，分别对应于 3个入射信号．利用本文方法对上述3个LFM信号进行二维DOA估计，重复进行50次独立实验，得到的估计结果如图3所示．

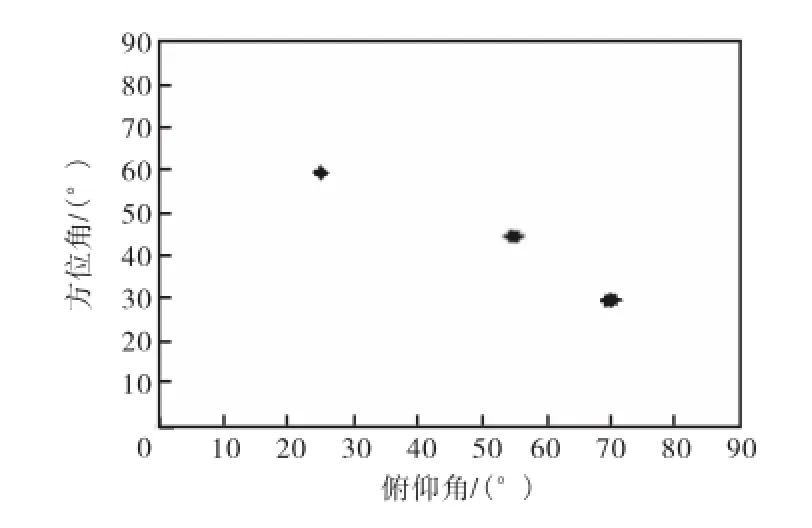
图3 入射信号的二维DOA估计结果Fig.3 2-D DOA estimation result of incident signals

另外，利用本文方法对3个入射信号的阵列响应向量 Ak(k=1，2，3)进行估计．为了评价估计精度，定义第k个信号的阵列响应的估计误差为

显然，有 0≤ERRk≤1成立．表 1给出了几种信噪比情况下的平均估计误差．

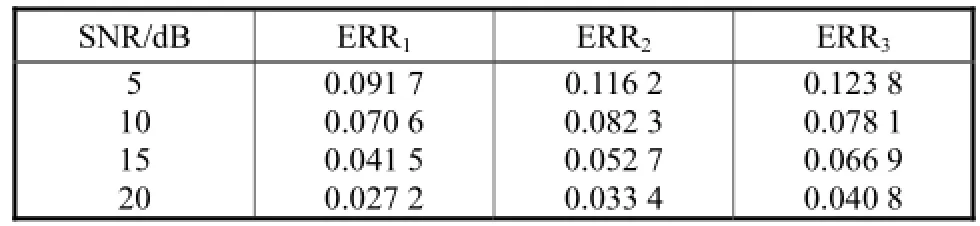
表1 阵列响应估计误差与信噪比的关系Tab.1 Estimation error of array response vs SNR

通过图 3和表 1可以看出，利用本文提出的方法，可以在非规则部分校准阵列条件下估计出多个LFM信号的二维DOA以及阵列响应，且具有较高的精度．

3.2 本文方法和传统方法的性能比较实验

采用 8阵元的双平行线阵，阵元间距 dx=dy= 10．入射信号以及其他各项参数的设置均和第3.1节相同．分别利用本文方法以及文献[9]提出的 FrFTESPRIT算法对各入射信号的二维 DOA进行估计．图4和图5分别给出了2种方法的DOA估计成功概率以及均方根误差(root mean square error，RMSE)随信噪比变化的曲线，所有仿真结果均为100次独立实验的平均．这里选择DOA估计的绝对误差小于 3°作为成功估计的标准，并定义第 k个入射信号的二维DOA估计的RMSE为

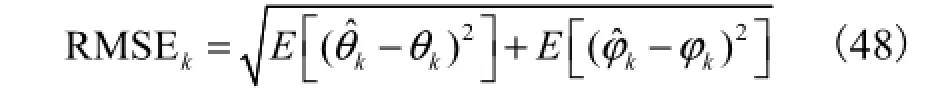
图4和图5表明，相比于传统方法，本文方法具有更低的信噪比门限．在 DOA估计的 RMSE相同时，与传统方法相比，本文方法可获得 6～8 dB的信噪比增益．

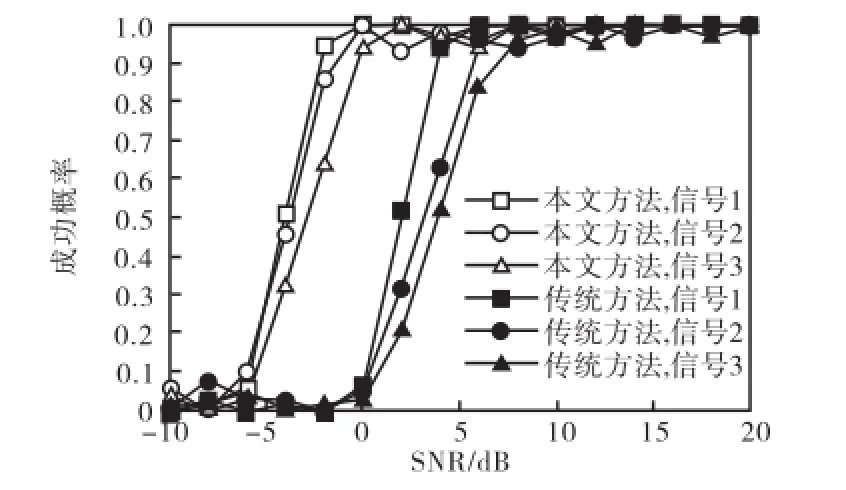
图4 DOA估计的成功概率随信噪比的变化曲线Fig.4 Success probability of DOA estimation versus SNR

图5 DOA估计的均方根误差随信噪比的变化曲线Fig.5 RMSE of DOA estimation versus SNR

4 结 语

本文提出了一种基于FrFT的宽带LFM信号二维DOA估计新方法．该方法通过更加复杂的空时联合采样结构挖掘观测信号所包含的有用信息，克服了传统方法对阵列结构以及阵元一致性的限制，且具有更好的空间分辨性能和更低的信噪比门限．此外，该方法无需谱峰搜索和二维参数配对过程，能够在估计信号二维DOA参数的同时获得相应的阵列响应，进一步扩展了其应用范围．仿真实验的结果证明了本文方法的有效性．

［1］ Chan Y K，Koo V C. An introduction to synthetic aperture radar[J]. Progress in Electromagnetics Research B，2008，2：27-60.

［2］ Gudra T，Herman K. Some problems of analyzing biosonar echolocation signals generated by echolocating animals living in the water and in the air[C]// Acoustics’08. Paris，France，2008：5941-5946.

［3］ Mason S，Berger C，Zhou S，et al. Detection，synchronization，and Doppler scale estimation with multicarrier waveforms in underwater acoustic communication[J]. IEEE Journal on Selected Areas in Communications，2008，26(9)：1638-1649.

［4］ Zhou Xin，Shi Yaowu，Yang Wenhong. 2-D DOA and polarization estimation of LFM signals with one electromagnetic vector sensor[C]//International Conference on Signal Processing. Beijing，China，2008：386-389.

［5］ Wen Zhong，Li Liping，Chen Tianqi，et al. Joint multiple parameters estimation for coherent chirp signals using vector sensor array[J]. Science in China Series F：Information Sciences，2008，51(1)：93-100.

［6］ 李立萍，黄克骥. 基于 STFT的相干宽带调频信号 2-D到达角估计[J]. 电子与信息学报，2005，27(11)：1760-1764.

Li Liping，Huang Keji. 2-D DOA estimation of coherent wideband FM signals based on STFT[J]. Journal of Electronics and Information Technology，2005，27 (11)：1760-1764(in Chinese).

［7］ 陶 然，周云松. 基于分数阶傅里叶变换的宽带 LFM信号波达方向估计新算法[J]. 北京理工大学学报，2005，25(10)：895-899.

Tao Ran，Zhou Yunsong. A novel method for the direction of arrival estimation of wideband linear frequency modulated sources based on fractional Fourier transform[J]. Transactions of Beijing Institute of Technology，2005，25(10)：895-899(in Chinese).

［8］ 杨小明，陶 然. 基于分数阶傅里叶变换的线性调频信号二维波达方向估计[J]. 电子学报，2008，36 (9)：1737-1740.

Yang Xiaoming，Tao Ran. 2-D DOA estimation of LFM signals based on fractional Fourier transform[J]. Acta Electronica Sinica，2008，36(9)：1737-1740(in Chinese).

［9］ 杨小明，陶 然. 基于分数阶 Fourier变换和ESPRIT算法的 LFM信号 2D波达方向估计[J]. 兵工学报，2007，28(12)：1438-1442.

Yang Xiaoming，Tao Ran. 2D DOA estimation of LFM signals based on fractional Fourier transform and ESPRIT algorithm[J]. Acta Armamentarii，2007，28 (12)：1438-1442(in Chinese).

［10］ Qi Lin，Tao Ran，Zhou Siyong，et al. Detection and parameter estimation of multicomponent LFM signal based on the fractional Fourier transform[J]. Science in China Series F：Information Sciences，2004，47(2)：184-198.

［11］ 田 达. 非平稳信号阵列多参量估计技术研究[D]. 成都：电子科技大学电子工程学院，2004.

Tian Da. Research on Array Processing for Multi-Parameter Estimation of Non-Stationary Signals[D]. Chengdu： School of Electronic Engineering，University of Electronic Science and Technology of China，2004(in Chinese).

［12］ 金 梁，殷勤业. 时空 DOA矩阵方法[J]. 电子学报，2000，28(6)：8-12.

Jin Liang，Yin Qinye. Space-time DOA matrix method [J]. Acta Electronica Sinica，2000，28(6)：8-12(in Chinese).

2-D DOA Estimation of Wideband LFM Signals in Partly Calibrated Irregular Array

LUO Peng，LIU Kai-hua，SHI Wei-guang，YAN Ge
(School of Electronic Information Engineering，Tianjin University，Tianjin 300072，China)

A novel 2-D direction of arrival(DOA)estimation method for wideband linear frequency modulation(LFM)signals was proposed. The incident signals were sampled in spatial domain and time domain synchronously，and a new time-frequency spatial DOA matrix was constructed based on the peak values of the observation samples in fractional Fourier domain. Moreover，the source DOAs were estimated by the eigen-decomposition process. Owing to sufficient mining of the time-frequency information included in observed signals，this method has a lower constraint of array structure，and can be applied to partly calibrated array with arbitrary geometry structure. Moreover，no spectral peak searching is needed in the method，and the parameters match automatically in the process. Simulation results show that the DOA estimation method in this paper can obtain 6—8 dB signal-to-noise ratio gain compared with the conventional method.

array signal processing；2-D DOA estimation；fractional Fourier transform；wideband LFM signal；partly calibrated array

TN911.72

A

0493-2137(2012)04-0325-06

2010-12-02；

2011-04-22.

国家自然科学基金资助项目(60872001).

罗 蓬（1984— ），男，博士研究生，luopeng1984@sohu.com.

刘开华，liukaihua@tju.edu.cn.