基于压缩感知的图像自适应编码算法

张淑芳，李 凯，徐江涛，瞿广财

(天津大学电子信息工程学院，天津 300072)

目前对图像信号进行采集和压缩普遍采用以香农定理为准则的处理方式，即对图像信号进行高速采样后再压缩编码．该采样方式要求采样速率达到信号带宽的2倍以上才能精确重构信号，对采样设备提出了巨大挑战；同时采用传统图像编码算法对采样后的数据进行压缩时，仅对采样数据变换后少数绝对值较大的系数进行压缩编码，抛弃大量零或者接近于零的系数，从而对采样资源造成大量浪费．近年来，由Candès[1]和 Donoho[2]提出的压缩感知(compressive sensing，CS)理论为新型图像采集和压缩处理提供了理论支持[3]，它首先利用随机观测矩阵Φ，把在某个正交基或紧框架上稀疏或可压缩的高维信号(x∈RN)投影到M维的低维空间上(得到测量值y)，然后通过求解优化问题从少量的投影中以高概率重构原始信号或图像．CS理论的核心思想是将压缩与采样合并进行，它突破了香农采样定理的瓶颈，即只需要通过少量的样本点就能够精确地重构原始图像，它将给信号处理带来一次新的革命，对统计学、信息论和编码等领域产生重要的理论影响[4]．

国内外学者对压缩传感在图像编码中的应用进行了大量研究．2006年 Haupt等[5]通过实验表明如果图像是高度可压缩的，测量过程即使存在噪声，压缩感知方法仍可准确重构图像．2006年Rice大学成功研制出“单像素相机”[6]，为低像素相机拍摄高质量图像提供了可能．2007年，Gan[7]借鉴离散余弦变换(discrete cosine transform，DCT)块编码的巨大成功提出了基于块的压缩感知方法，每一块都采用相同的块观测矩阵，可减少观测矩阵的存储量，有效解决高维图像采集问题．由于在一幅图像中每个块在变换域的稀疏度不一样，在变换域越稀疏的块，重构图像所需要的采样点数就越少．本文鉴于此，提出了基于压缩感知的图像自适应编码算法，在对图像进行CS压缩采样前，首先判断其在 DCT域的稀疏度，然后根据每个块的稀疏度对其进行自适应的压缩采样，从而使得在低采样率的情况下能够对图像进行高质量重构．

1 压缩感知理论

压缩感知理论由 Candès和 Donoho[1-2]在 2006年正式提出．Candès证明了只要信号在某一正交空间具有稀疏性，就能以较少的采样点数完全或者以很高概率重建该原始信号．

假设 x =[x( 1 ),x( 2),… ,x (N)]T表示一维离散时间信号组成的列向量，其可表示为一组标准正交基的线性组合，即

式中：Ψ 为基矩阵，Ψ = [ψ1,ψ2,… ,ψN]，ψi为列向量；N × 1 的列向量s是x的加权系数序列，即s = x ,ψ =x ．显然，x和s是同一个信号的等价ii表示，x是信号在时域的表示，s则是信号在Ψ域的表示．如果s中只有 K个非零(或绝对值较大)的系数，其余 N-K个系数都为 0(或绝对值很小)，则称s为信号x的稀疏表示．

假设 y ∈RN为信号x在测量矩阵Φ∈RM×N下的线性测量值，即

式中：=ΘΦΨ是一个MN×的矩阵．对于给定的测量值y从式(2)求解s是一个线性规划问题，但由于KMN≪≤，即方程的个数少于未知数的个数，这是一个欠定问题．Candès等[8]证明了信号重构可以通过求解最小l0范数来求解，如果测量矩阵Φ和稀疏变换矩阵Ψ满足约束等距性(restricted isometry property，RIP)条件，最优稀疏解ˆ可以由测量值y∈RN重构，即

式中 ·0为向量的 l0范数，代表向量x中非零元素的个数．该式为非凸优化问题，是典型的 NP-hard问题，计算复杂度高．Candès[1]和 Donoho[2]提出用 l1范数来代替 l0范数，把式(3)转化为一个凸优化问题来求解，即

得到信号x在稀疏域Ψ下的最优稀疏解ˆs后，信号x的重构值ˆx可表示为

在对图像进行稀疏变换时，常用 DCT、小波变换和有限差分来作为变换稀疏基，在用有限差分做稀疏变换时，常用全变差(total variation，TV)来衡量．Candès等[9]从大量自然图像的离散梯度都是稀疏的角度出发，提出了适合二维图像压缩重构的最小全变分法，重构精确而且鲁棒性强，但是运算速度较慢．2009年Li[10]提出了基于最小全变分法的 TVAL3算法，它将全变分法和增广拉格朗日函数相结合来进行图像压缩重构，有效提高了重构速度，并且重构图像的PSNR值也有了很大提高，其重构公式为

式中：p＝1或p＝2代表1范数或2范数；gradiu表示在位置i处u的离散梯度向量．

因此，本文在对图像进行自适应压缩编码后，利用测量值进行图像重构时选用TVAL3算法．

2 基于压缩感知的图像自适应编码算法

本文提出了基于压缩感知的图像自适应编码算法，根据图像各个块的稀疏度对其进行自适应的压缩采样，从而实现低采样率下图像的高质量重构．

2.1 图像压缩采样率对重构质量的影响

本文对图像进行基于块的压缩采样，把图像分为3232×的块，为了满足RIP条件，本文使用独立同分布的高斯随机矩阵作为测量矩阵Φ，分别对图像进行 20%、40%、60%和 80%的采样，并采用 TVAL3算法对测量值进行重构．为了衡量图像重构效果，采用客观图像质量评价指标 PSNR来表征重构图像块和相应原始图像块之间的差别．图 1(a)和(b)分别为Lena图像和Cameraman图像在不同采样率下每幅图像各个块 PSNR值的分布情况，块采用从上到下，从左到右的方式进行排列，横坐标表示块的分布，纵坐标表示重构图像各个块的PSNR值．

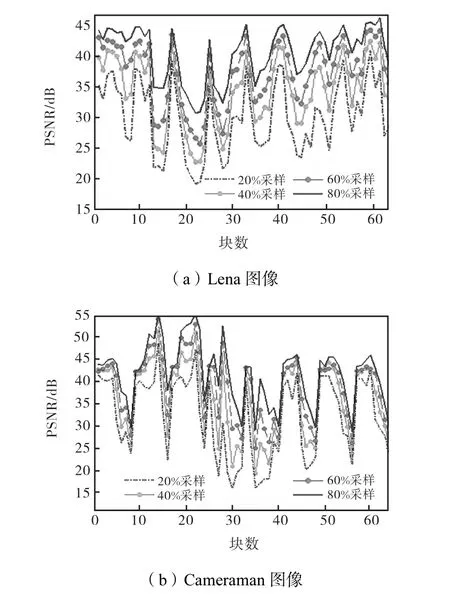
图1 不同采样率下重构图像PSNR值的分布Fig.1 PSNR distribution of reconstructed images at different sampling rates

从图 1可以看出，随着采样率的升高，各个块的PSNR值呈上升趋势，但高采样率会导致图像压缩效率的降低，并且造成解码端图像重构复杂度的升高．因此，需要在图像采样率和 PSNR之间形成良好的折中．另外，由于图像中各个块的稀疏度不同，使得在相同采样率下重构图像中各个块的 PSNR值有较大起伏，对图像整体质量造成了很大影响．

图2为20%和80%采样率时的重构图像，其中图2(a)为采样率20%的重构图像，由于其PSNR起伏较大，有些块 PNSR较好，有些块 PSNR较差，因此其块效应比较明显，在脸部和帽子区域可以看出明显的块效应．图 2(b)为采样率 80%的重构图像，虽然PSNR起伏也较大，但由于其 PSNR值都较高，因此看不出明显的块效应，其重构时间比采样率20%时的重构时间大约增加了50%．

因此，需要对整幅图像进行自适应的压缩采样，对稀疏性较好的块采用较低的采样率，对稀疏性较差的块采用较高的采样率，从而确保在较低的采样率下，整幅图像重构质量达到最优．如果能找到图像各个块的PSNR和稀疏度之间的关系，就能对图像进行自适应的压缩采样．

图2 不同采样率下的重构图像Fig.2 Reconstructed images at different sampling rates

2.2 图像稀疏度的判断准则

由于对图像进行分块二维 DCT变换后，低频系数分布在 DCT分块系数矩阵的左上角，高频系数分布在其右下角，并且低频系数的绝对值大于高频系数的绝对值．图像越稀疏，它的低频部分占的比重就会越大．本文利用α作为 DCT系数绝对值|Ti,j|大小的判断阈值，如果|Ti,j|小于α则判定其为较小的系数，反之则把该系数作为较大的DCT系数．利用C表示图像各个块 DCT变换系数中模值小于α的个数．从以上分析可知，C值越大表示该块越稀疏，其需要较少的压缩采样点数就能得到较好的重构图像[11]．图3(a)和(b)分别给出了α＝4，采样率为 40%时，Lena和Cameraman重构图像中各个块C值和PSNR值的关系．

从图 3可以看出，图像各个块的 C值和 PSNR值大致服从相同的变化规律，即块的 C值越大，其PSNR值越高，因此可通过C值来间接表征图像块重构时能够达到的PSNR值．

因此，本文以C值作为图像稀疏度的判断准则，依据 C值的大小来对图像的采样率进行自适应选择．

2.3 基于压缩感知的图像自适应编码算法

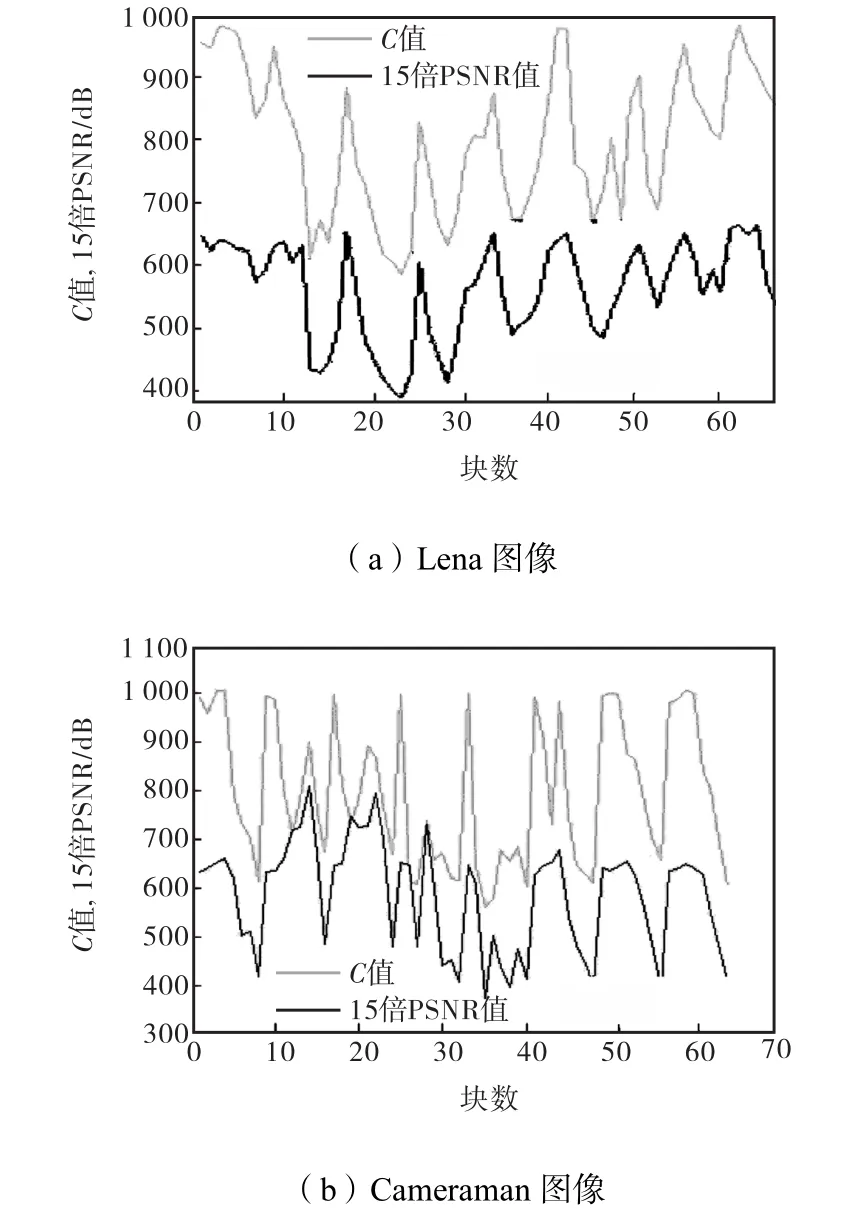
图3 图像各块C值和PSNR值之间的关系Fig.3 Relationship between C and PSNR of each block in the image

为了在较低采样率下获得较高的图像质量，本文对C值较大的块以较低采样率进行压缩采样，反之对C值较小的块以较高采样率进行压缩采样，从而保证整幅图像都具有较高的重构质量．本文选用iT(i＝1，2，3)作为对原始图像进行压缩采样时采样率高低判断的阈值，且 T1＞T2＞T3；用β1、β2、β3和β4分别表示对图像进行 20%、40%、60%和 80%的采样压缩．依据 C和 Ti的大小关系，对每个图像块进行自适应的压缩采样，即

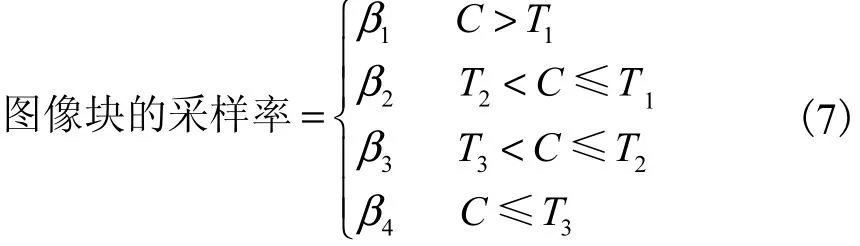
Ti取值不同，则会对图像的压缩效率和重构质量产生不同影响．当 Ti取值较小时，图像可以较低的采样率进行压缩采样，从而可有效提高图像的编码效率，降低编码器的功耗，但重构图像的质量要差一些；反之，当 Ti取值较大时，图像编码效率较低，但重构图像的质量较好．大量实验表明，当 T1、T2和 T3的取值分别为900、800和700时，在保证重构图像质量较好的前提下，能较大幅度提高图像的编码效率．在应用本文所提算法对图像进行自适应编码时，需要根据网络带宽、编码器的功耗和对图像重构质量的要求等实际因素对 Ti的取值进行相应调整．

对图像进行自适应压缩采样的流程如图4所示．

步骤1 将输入图像分成m个n×n的块，并令i＝1．

步骤 2对第i块图像进行DCT变换并计算该块的C值．

步骤 3根据式(7)，判断 C值和图像压缩采样阈值T1、T2和T3的关系，如果C＞T1，则对图像进行1β采样，转向步骤7，否则执行步骤4．

步骤4 如果C≤T1并且C＞T2，则对图像进行2β采样，转向步骤7，否则执行步骤5．

步骤5 如果C≤T2并且C＞T3，则对图像进行3β采样，转向步骤7，否则执行步骤6．

步骤6 如果C≤T3，则对图像进行4β采样．

步骤 7 如果 i≥m 则结束整个压缩采样过程，否则，令 i＝i＋1，重新执行步骤 2．

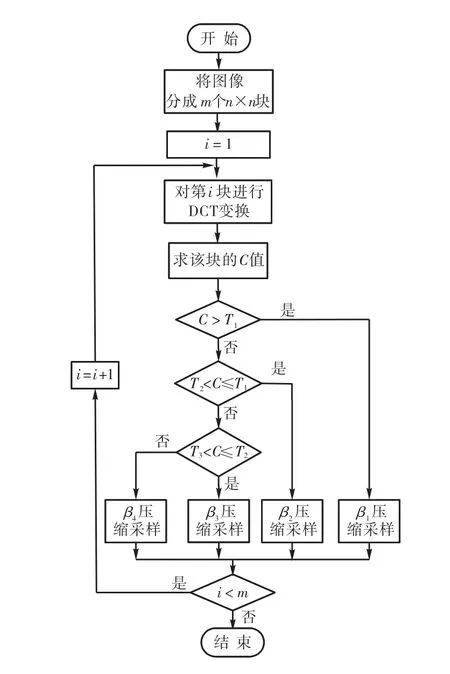
图4 算法流程Fig.4 Flow chart of the proposed algorithm

为了提高压缩效率，本文在对图像块进行压缩采样时，利用相同的种子针对各个块不同的采样率生成相应尺寸的高斯随机观测矩阵，这就与传统固定采样率的压缩方法一样，仅需向解码端传递一次产生随机观测矩阵的种子．同时，为了向解码端传递各个块压缩时所使用的采样率，本文使用标志位 1、2、3和 4分别表示 20%、40%、60%和 80%的采样率，与传统利用固定采样率对图像进行压缩采样相比，该自适应算法只需在各图像块编码码流的开始多加入一个采样率标志位即可．

3 实验结果及分析

采用Lena、Cameraman和Columbia具有不同灰度和纹理细节的图像对所提算法的有效性进行验证，其中 Lena图像包含丰富的细节信息和纹理特征；Cameraman图像前景和背景对比度较大；Columbia为景物图像，平滑和细节区域区分较为明显.

在实验中，块的大小 n取值为 32，α的取值为4，采用 TVAL3恢复算法，并且阈值 T1、T2和 T3的取值分别为 900、800和 700，实验结果如表 1所示．其中λ表示采样率的增加所带来的PSNR增益，以20%时的采样率1β和PSNR1作为基准，其余采样率所带来的PSNR增益可表示为

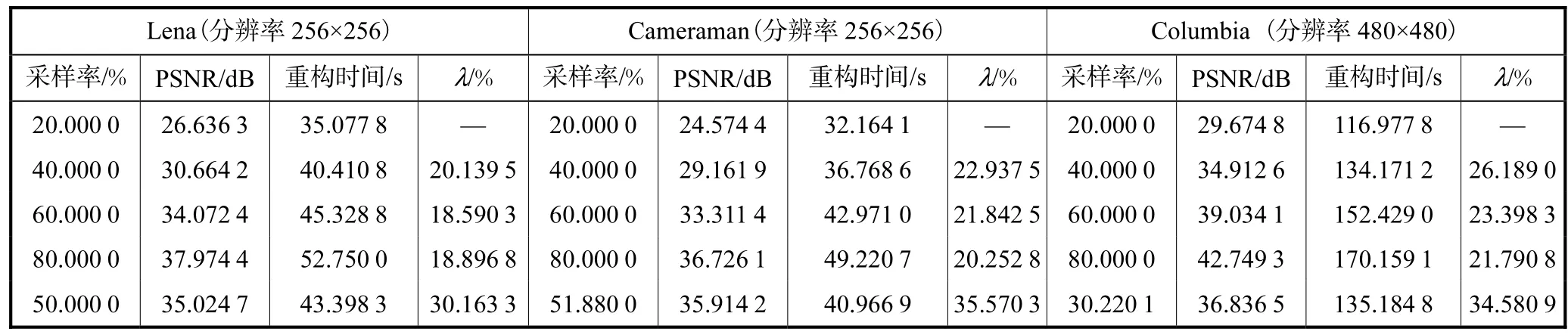
表1 实验结果Tab.1 Experimental results

从表 1可以看出，固定采样率下，增加单位采样率所能提升的PSNR值的增益在20%左右，而本文提出的自适应采样算法增加单位采样率所能带来的图像 PSNR值平均增益达到了33%．显然，本算法对重构图像的质量有显著提高．对于Lena和 Cameraman图像，包含的细节信息较多，采用本文所提自适应算法所需采样率大约为50%，对于前景和背景区域区分较为明显的 Columbia图像，采用自适应算法时所需采样率仅为 30.22%，这是由于大部分背景区域块的稀疏性较好，采用较低的采样率就能精确重构图像．

图5给出了Lena原始图像以及不同采样率下的重构图像．其中图 5(e)为原始图像，图 5(a)、(b)、(c)和(d)分别为 Lena图像在采样率 20%、40%、60%和 80%时的重构图像，随着采样率的增加，重构图像的主观质量越来越好．当采样率为 20%和 40%时，存在明显的块效应和模糊现象；当采样率达到 60%时，重构图像的 PSNR值为 34.07,dB，从主观效果上来看，重构图像和原始图像的差别很小．采用本文自适应采样算法，仅需要 50%的采样率，重构图像(图5(f))的PSNR值为35.02,dB，和原始图像相比，几乎看不出差异．

图5 Lena原始图像以及在不同采样率下的重构图像Fig.5 Original image and reconstructed images at different sampling rates for Lena

为了更加直观地说明利用自适应算法进行压缩采样时图像各区域所选用的采样率，图 6(a)和(b)分别给出了 Lena图像和 Cameraman图像采样率的分割示意．在图 6(a)所示的 Lena图像分割图中，对于头发、面部和帽子这些包含细节信息较多的区域，图像块的稀疏性较差，采用较高采样率对此进行压缩采样，有效保证了重构图像的主客观质量，而对于周边比较平滑的区域，图像块的稀疏性较好，则采用 20%的采样率，可有效提高图像的压缩效率．同样对于图6(b)所示的 Cameraman图像而言，在草坪、人的头部和相机等部位，包含的纹理信息较多，采用了 80%的采样率进行压缩采样，而对于天空这些比较平坦的背景区域，块的稀疏性较好，采用 20%采样率进行压缩采样．

图6 图像采样率的分割示意Fig.6 Partition sketch map of image sampling rates

图7 给出了Lena图像在各种固定采样率和自适应算法下各个块的PSNR值分布，其中横坐标表示块的分布，采用和图 1相同的排列方式；纵坐标表示PSNR值的大小．从图 7可以看出，与固定采样率的PSNR曲线相比，本文所提自适应算法的PSNR曲线较平坦，上下起伏较小，从而保证整幅图像中各个块的重构质量都位于一个平均水平，显著提高了重构图像的整体质量．

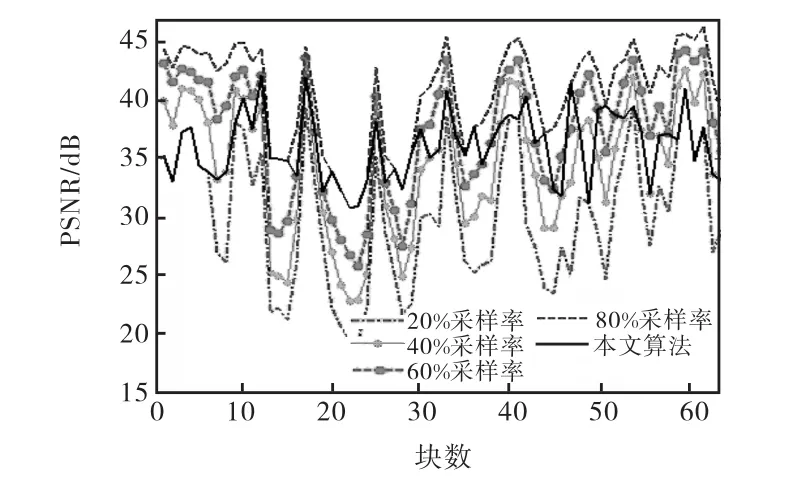
图7 Lena图像各个块的PSNR分布Fig.7 PSNR distribution of each block in Lena image

4 结 语

本文提出了一种基于压缩感知的图像自适应编码算法，该算法根据图像各个块在 DCT域的稀疏度，分别对各个块进行不同采样率的压缩采样，在确保整体图像质量较优的条件下，有效降低了图像的编码码率．实验结果表明，本文所提算法实现复杂度较低，重构图像主客观质量较好．

［1］ Candès E J. Compressive sampling[C]// Proceedings of the International Congress of Mathematicians. Madrid，Spain，2006：1433-1452．

［2］ Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory，2006，52(4)：1289-1306.

［3］ 李树涛，魏 丹. 压缩传感综述[J]. 自动化学报，2009，35(11)：1369-1377.Li Shutao，Wei Dan. A survey on compressive sensing[J]. Acta Automatica Sinica，2009，35(11)：1369-1377(in Chinese).

［4］ 石光明，刘丹华，高大化，等. 压缩感知理论及其研究进展[J]. 电子学报，2009，37(5)：1070-1081.Shi Guangming，Liu Danhua，Gao Dahua，et al. Advances in theory and application of compressed sensing[J]. Acta Electronica Sinica，2009，37(5)：1070-1081(in Chinese).

［5］ Haupt J，Nowak R. Compressive sampling vs. conventional imaging[C]// Proceedings of the IEEE International Conference on Image Processing. Atlanta，Georgia，2006：1269-1272.

［6］ Takhar D，Laska J N，Wakin M B，et al. A new compressive imaging camera architecture using opticaldomain compression[C]// Computational Imaging IV at SPIE Electronic Imaging. San Jose，California，2006：43-52.

［7］ Gan L. Block compressed sensing of natural images[C]//Proceedings of the 15th International Conference on Digital Signal Processing. Washington DC，USA，2007：403-406.

［8］ Candès E J，Tao T. Decoding by linear programming[J].IEEE Transactions on Information Theory，2005，51(12)：4203-4215.

［9］ Candès E J，Romberg J，Tao T. Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory，2006，52(2)：489-509.

［10］ Li Chengbo. An Efficient Algorithm for Total Variation Regularization with Applications to the Single Pixel Camera and Compressive Sensing[D]. Houston：Department of Computational and Applied Mathematics，Rice University，2009.

［11］ Stanković V， Stanković L ， Cheng S. Compressive video sampling[C]// Proceedings of the European Signal Processing Conference. Lausanne，Switzerland，2008.