薄壁变截面高桥墩的稳定分析

唐扬斌



薄壁变截面高桥墩的稳定分析

唐扬斌

(湖南常德公路工程总公司, 湖南 常德, 415000)

应用里兹法研究了考虑墩身自重的薄壁变截面高桥墩的稳定性. 构造满足桥墩位移边界条件的横向位移曲线函数, 得到其应变能和荷载势能表达式. 基于势能驻值条件求出了薄壁变截面高桥墩的临界荷载解析式, 利用该解析式可以方便地求出薄壁变截面高桥墩的临界荷载. 与有限元分析得到临界荷载的比较表明, 该方法简单可靠.

里兹法; 变截面高桥墩; 稳定; 临界荷载

目前我国公路建设已经深入到祖国的边远山区, 跨越深谷的桥梁日益增多, 这使得高桥墩应用也越来越多, 墩高经常达到30~60 m, 甚至更高[1-2]. 另外, 随着高强混凝土的应用, 高强材料的出现, 以及出于节省材料和降低工程造价的需要, 高桥墩通常做成薄壁变截面的. 对于薄壁变截面高桥墩的设计和施工, 除了必须考虑其强度满足要求外, 稳定性也是必须考虑的重要因素[3-4]. 高桥墩的稳定性问题实质就是压杆的稳定问题, 对于等截面高桥墩的稳定性, 目前已得到比较充分的研究, 有现成的等截面压杆临界荷载计算公式计算其临界荷载, 而对于变截面高桥墩的稳定性, 目前通常采用通用有限元软件计算其临界荷载. 如刘庆潭采用传递矩阵法研究了锥形变截面压杆稳定[5]; 卞敬玲采用有限单元法研究了任意变截面压杆的分支屈曲[6]; 楼梦麟采用模态摄动法得到了变截面压杆稳定问题半解析解[7]; 宋嘉考虑初始缺陷和多种荷载的作用[8]; 杜进生考虑施工缺陷和初始偏心的影响[9]; 赵延安考虑桥墩结构形式的影响[10], 研究了高桥墩的稳定性问题. 采用有限元软件计算薄壁变截面高桥墩的临界荷载时, 需要耗费较多机时用来建模和计算, 这不利于其工程应用, 因此需要提出用以探求薄壁变截面高桥墩临界荷载的比较简便的方法. 相对于有限单元法, 解析法由于能得到结构临界荷载的解析表达式, 更利于工程应用. 本文应用里兹法计算了考虑墩身自重的薄壁变截面高桥墩的临界荷载. 该方法理论简单, 计算方便, 结果可靠, 可以求解不同支承情况薄壁变截面高桥墩的弹性稳定, 应用范围广泛, 具有广阔的应用前景.

1 基本公式推导

如果桥梁上部结构对桥墩约束较大, 而基础又较软, 不能限制桥墩的转动时, 此时可以把桥墩的边界条件视为两端简支. 现在研究考虑桥墩自重的两端简支变截面高桥墩的临界荷载. 如图1所示两端简支的变截面高桥墩, 桥墩高为, 设桥墩底部截面对弱轴的惯性矩为0, 上部结构传给桥墩顶部的荷载为. 以变截面高桥墩底部截面中心为坐标原点,轴为高桥墩纵向对称轴,轴平行底部截面, 建立如图所示坐标系. 设纵坐标为的截面对弱轴的惯性矩为:

式中, a、b、c是待定常数, 可以根据桥墩截面变化规律得出.

设纵坐标为的截面桥墩质量产生的轴向压力为:

如图1所示两端简支的桥墩边界条件为:

因而可设高桥墩的横向位移曲线为:

将式(4)对求导, 得

设桥墩材料的弹性模量为, 对应横向位移()桥墩的应变能为:

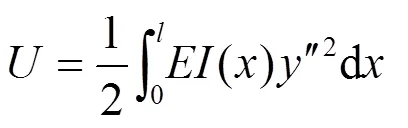
将式(1)、式(5)代入式(6), 可以得到桥墩的应变能为:

桥墩的荷载势能为:

将式(2)、式(5)代入式(8), 得

桥墩的总势能为:

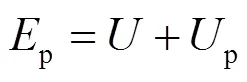
根据势能驻值条件有

将式(7)、式(9)代入式(10), 再将式(10)代入式(11), 得

由式(13)可以得到如图1所示两端简支的变截面高桥墩临界荷载特征方程:

方程(14)中最小的解即为考虑自重的变截面高桥墩临界荷载, 即:

2 算例分析

依题意, 可以求得纵坐标为的截面对弱轴(平行于横桥向)的惯性矩为:

纵坐标为的截面桥墩质量产生的轴向压力为:

由式(1)-式(2)和式(16)-式(17)可知,=8.538 3×10-9,=-1.844 3×10-4,=1,=9.375×10-7,=-0.045,= 249.6. 将相关参数代入式(14)、式(15), 则可以求得该混凝土变截面高桥墩临界荷载pcr=182 669.2 kN, 为了验证本文方法, 采用ANSYS计算该混凝土薄壁变截面高桥墩的临界荷载pcr=177 919.8 kN, ANSYS计算结果比本文方法稍小, 二者误差为2.67%, 表明本文方法有很好的精度. 另外, 令===0, 即不考虑墩身自重对薄壁变截面高桥墩的稳定性的影响, 由式(14)、式(15)可以求得pcr=182 669.4 kN, 比考虑自重时薄壁变截面高桥墩的临界荷载182 669.2 kN稍大, 但二者差别很小, 可以忽略不计, 究其原因是本文所研究的对象是薄壁变截面高桥墩, 由于薄壁, 其自重本身不大, 所以其对稳定性的影响很小.

图2 一端固定一端简支的变截面高桥墩

依题意, 可以求得纵坐标为的截面对弱轴(平行于横桥向)的惯性矩为:

高桥墩纵坐标为的截面处受自重产生的轴力为:

设高桥墩的横向位移曲线为:

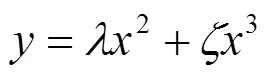
在式(20)中，对求导, 得

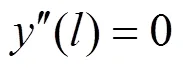
将式(18)、式(21)和式(22)代入式(6), 可以得到桥墩的应变能为:

将式(19)、式(21)和式(22)代入式(8), 可以得到桥墩的荷载势能为:

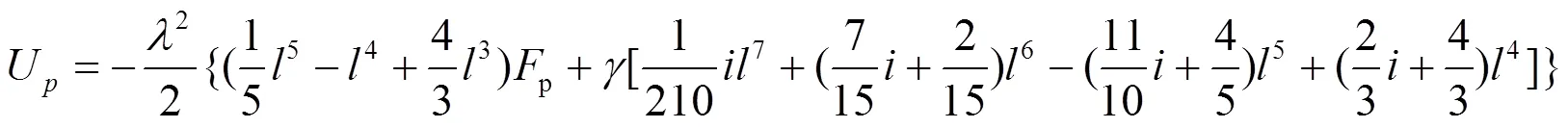
给定坡度、墩高, 由式(25), 可以计算如图2所示混凝土薄壁变截面高桥墩的临界荷载, 如表1所示. 为了验算本文方法, 采用ANSYS软件计算出了该高桥墩的临界荷载, 也列在表1中. 从表1可以看出, 本文方法与ANSYS软件的计算结果相差不大, 表明本文方法有很好的精度. 另外, 本文的计算结果略大于有限元计算结果(算例1也具有这个规律), 这是因为里兹法使结构由无限自由度体系转化为有限自由度体系, 相当于对体系施加了某种约束.

表1 混凝土薄壁变截面高桥墩的临界荷载

3 结论

对于薄壁变截面高桥墩, 由于截面面积较小, 桥墩较高, 对其进行稳定分析是必须的. 针对薄壁变截面高桥墩的不同约束情况, 本文应用里兹法计算了考虑桥墩自重的薄壁变截面高桥墩的临界荷载. 只要高桥墩的横向位移曲线假设足够精确, 本文的计算结果是很可靠的, 两个算例也验证了本文方法的可靠性. 由于里兹法假设横向位移曲线时使结构由无限自由度体系转化为有限自由度体系, 相当于对体系施加了某种约束, 所以采用里兹法计算的临界荷载略大于真实临界荷载, 但误差不大, 完全可以满足工程精度.

[1] 李文华, 贺拴海, 鲁洁. 高墩大跨弯连续刚构桥空间稳定性的解析解[J]. 西安建筑科技大学学报: 自然科学版, 2011, 43(1): 36-43.

[2] 董晓梅, 马强. 高墩大跨径连续刚构桥墩身稳定分析[J]. 交通科技, 2009(2): 4-7.

[3] 齐宏学. 装配式梁桥高墩计算长度系数探讨[J]. 公路, 2011, (11): 51-55.

[4] Raafat E S Ismail, Fahmy A Fathelbab, Hesham A Zien Eldin, et al. Numerical investigations on dynamic performance of stiffened box steel bridge piers[J]. International Journal of Steel Structures, 2012, 12(2): 139-155.

[5] 刘庆潭. 含锥形变截面压杆稳定计算的传递矩阵法[J]. 计算结构力学及其应用, 1996, 13(3): 364-368.

[6] 卞敬玲, 王小岗. 变截面压杆稳定计算的有限单元法[J]. 武汉大学学报: 工学版, 2002, 35(4): 102-104.

[7] 楼梦麟, 李建元. 变截面压杆稳定问题半解析解[J]. 同济大学学报: 自然科学版, 2004, 32(7): 857-860.

[8] 宋嘉, 张敏, 李银斌. 考虑初始缺陷和多种荷载作用的高墩稳定性分析[J]. 重庆交通大学学报: 自然科学版, 2012, 31(2): 199-202.

[9] 杜进生, 康景亮, 罗小峰. 考虑施工缺陷和初始偏心的高墩稳定性分析[J]. 工程力学, 2011, 28(S1): 115-118.

[10] 赵延安, 罗小峰, 刘海彬, 等. 桥墩结构形式对小花沟连续刚构桥高墩稳定性影响分析[J]. 公路, 2011, (11): 65-69.

Stability analysis of thin-walled high bridge piers with variable section

TANG Yang-bin

(Hunan Changde Highway Engineer General Company, Changde 415000, China)

Taking the dead weightof the pier effect into consideration, it was studied that the stability of thin-walled high bridge piers with variable cross-section using Ritz method. First, the function of pier lateral displacement curve was constructed which meet the displacement boundary conditions. Then the expression of strain energy and external load potential energy was got. Finally, the stability critical load formula of thin-walled high bridge piers with variable cross-section was deduced derived from the potential energy stationary value condition. And the critical load of thin-walled high bridge piers with variable cross-section could be conveniently calculate with the formula. The comparison of the results using this method and finite element analysis indicates that the method is simple and valid.

Ritz method; thin-walled high bridge piers with variable section; stability; critical load

10.3969/j.issn.1672-6146.2012.03.022

U 443.22

1672-6146(2012)03-0077-05

2012-07-23

唐扬斌(1975-), 男, 工程师, 主要从事公路与桥梁施工管理工作. E-mail: 2411745649@qq.com.

(责任编校:刘刚毅)