关于方程
2012-05-11管训贵
管训贵
管训贵
(泰州师范高等专科学校 数理信息学院, 江苏 泰州, 225300)


1 引言及主要结论
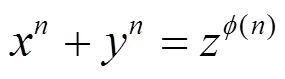
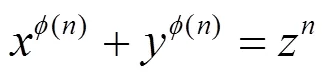
的求解问题.
本文完整地讨论了方程(2)的正整数解的存在性, 即证明了以下一般性的结果.
2 关键性引理
证明 可参见文献[4-5].
证明 可参见文献[6-7].

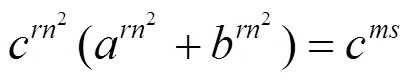


3 定理1的证明
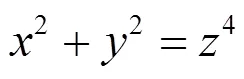
由引理1知, 方程(6)有无穷多组正整数解, 从而方程(2)有无穷多组正整数解.

由引理2知, 方程(7)无正整数解, 从而方程(2)无正整数解.
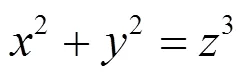
由引理1知, 方程(8)有无穷多组正整数解, 从而方程(2)有无穷多组正整数解.
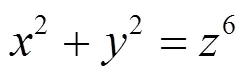
由引理1知, 方程(9)有无穷多组正整数解, 从而方程(2)有无穷多组正整数解.
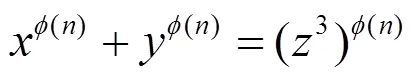
由引理2知, 方程(10)无正整数解, 从而方程(2)无正整数解.

由引理2知, 方程(11)无正整数解, 从而方程(2)无正整数解.
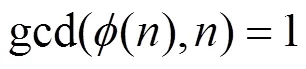
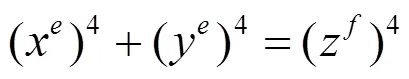
由引理2知, 方程(12)无正整数解, 从而方程(2)无正整数解.
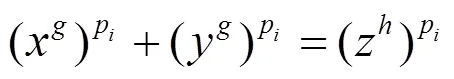
由引理2知, 方程(13)无正整数解, 从而方程(2)无正整数解.
综上, 定理1得证.
[1] Sandor J. Open question 2126[J]. Octogon Math Mag, 2006, 14(1): 409-412.

[4] Mordell L J. Diophantine equations[M]. London: Academic Press, 1969.
[6] Wiles A. Modular elliptic curves and Fermat’s Last Theorem[J]. Ann of Math, 1995, 141(3): 443-551.
[7] Taylor R, Wiles A. Rings-theoretic properties of certain Hecke algebras[J]. Ann of Math, 1995, 141(3): 553-572.
GUAN Xun-gui
(School of Mathematics Physics and Information Science, Taizhou Normal College, Taizhou 225300, China)
Diophantine equation; criterion; Fermat’s Last Theorem; positive integer standard factorization into prime number
10.3969/j.issn.1672-6146.2012.03.002
O 156
1672-6146(2012)03-0006-02
2012-06-14
泰州师范高等专科学校重点课题资助项目(2011-ASX-01)
管训贵(1963-), 男, 副教授, 主要研究方向为基础数论. E-mail: tzszgxg@126.com
(责任编校: 刘晓霞)
