数学建模解的分析与检验

曲孝海, 梅汉飞



数学建模解的分析与检验

曲孝海, 梅汉飞

(湖南文理学院 数学与计算科学学院, 湖南 常德, 415000)

实际应用中, 数学模型是否合适, 必须对其解的意义进行分析、检验. 为进一步优化模型, 从量纲一致性分析、参数灵敏度分析、临界值分析、假设合理性检验分析、误差分析几方面探讨了模型的分析. 模型检验主要包括实际可行性检验, 模型的改进与完善.

数学建模; 灵敏度分析; 模型改进

数学是在实际应用中产生的, 要解决实际问题必须建立数学模型[1], 数学建模工作始于现实世界, 并终于现实世界, 最终得到实际问题的解答. 所建模型是否合适？模型的解是否合理？这个解说明了什么问题？因此必须对解的意义进行分析、检验, 这样才能发现影响模型不合适的因素, 本文主要探讨数学建模解的分析和检验.

1 模型分析

模型分析主要是对模型的解进行数学分析. 有时分析解的可行性、实际意义, 变量间的依赖关系; 有时要根据模型做出预测、最优决策或控制. 不论哪种情况还需要进行误差分析, 稳定性或灵敏度分析等[2-3].

假设石头下降时所受空气的阻力和速度成正比, 因而阻力产生的加速度和速度也成正比, 设比例系数为.

此模型是否合适, 必须对其进行检验分析.

1.1 量纲一致性分析

量纲分析是20世纪初提出的在物理领域中建立数学模型的一种方法, 是对所涉问题有一定了解, 在实验和经验的基础上利用量纲齐次原则来确定各物理量之间的关系. 在数学的应用中, 需处理的往往不是“纯粹的”数, 而是反映事物某一特性的度量. 用数加单位来表示具体度量; 用量纲的概念来表示被度量的特性, 在模型中单位必须统一.

由的定义, 可推得的量纲为T-1, 由模型也可推得[]=T-1. 可见模型的量纲统一是必须的, 但仅凭量纲分析能否确定模型合适呢？还要从其他方面进行分析.

1.2 参数灵敏度分析

在建模过程中, 需要考虑各种与研究对象有关的因素. 有些因素是以变量参数的形式出现的, 模型对这些参数的敏感性反映了各种因素影响模型的显著程度; 有些因素在进行假设时认为是常量, 但不能保证其完全符合实际, 对这些参数进行灵敏度分析有助于模型的改进和应用.

通过本底和测量效率的数据分析，最终选择道址范围为 100～350，在此范围内 FM值处于较高值，本底相对较低。在100～350的道址范围内进行淬灭—效率曲线绘制（见图2），拟合公式的 R2值都在 0.98以上。利用拟合公式，结合各点的SQP（E）值进行效率计算，测量效率与计算效率偏差都在±2%范围内（见表5）。

1.3 假设合理性分析

假设是建模的已知条件, 假设是否合理是建立模型的关键. 事实上, 有观点认为: 模型就是假设. 假设决定了模型的方向, 假设与现实的相容度决定了模型的价值.

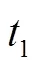
通过对模型的检验分析, 发现由于模型假设不合理, 考虑因素不合适, 造成模型不合理, 需要重新分析问题建立数学模型.

1.4 参数或变量的临界值分析

临界值分析同样是检验模型合适的重要手段. 分析参数或变量的临界值同样可以看出模型的合理性. 马尔萨斯人口模型:

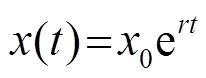
1.5 误差分析

作为对实际问题的近似刻画, 数学建模的结果与实际会或多或少的存在一定误差. 一方面要根据建模目的确定允许的误差范围; 另一方面, 要分析误差来源.

a.误差来源

误差是由于数据观测造成的？还是由于模型的不完善、近似求解方法和计算工具的舍入造成的？这就需要对偏差的分布进行统计分析. 若误差服从均值为0, 方差很小的正态分布, 表明模型很好地反映了实际情况. 否则, 需进一步修正模型, 可通过假设检验来验证.

假设检验步骤:

b) 在原假设成立的条件下, 构造一个分布已知的统计量;

b. 误差范围

数据在测量中不可避免地存在由于仪器或人为因素而产生误差. 由于误差的传递, 依赖于原始数据的模型的结果必然有一定的不准确度. 因此, 估计误差的范围是必要的. 一般采用的计算公式是: 结果的标准差是每个观测值的标准差的平方和的算术平方根. 对于其他误差来源, 可以通过对相应变量和参数的灵敏度分析, 确定误差的允许范围.

2 模型检验

2.1 实际可行性检验

模型检验是分析所得结果的实际意义, 与实际情况进行比较, 看是否符合实际, 若结果不够理想, 应该修改, 补充假设或重新建模, 有些模型需要经过多次反复, 不断完善. 把数学上分析的结果回到实际问题, 并用实际的现象、数据与之比较, 或运行模型, 检验模型的合理性和适应性, 即可进行实际可行性检验. 例如可进行预测性检验.即借用所建模型, 用历史预测现实, 以验证模型的准确度.

表1 模型改进

2.2 模型的改进

经模型的检验分析, 发现模型不完善, 必须通过解释、验证、修改等多次反复, 对其进行改进, 最终达到理论与实践的统一[4-5]. 例如, 人口模型、传染病等模型都是在反复改进中形成的. 考虑诸多方面, 模型的改进与完善可按表1进行.

3 结论

本文详细探讨了模型解的分析、检验以及模型的完善, 不仅有利于模型的建立, 还有利于更好的解决实际问题. 这对数学建模的教与学、对于工程技术工作者来说, 具有重要的参考、指导意义.

[1] 潘春平. 网络环境下高职数学建模过程与教学研究[J]. 南昌教育学院学报, 2012, 27(3): 99-100.

[2] 宋瑞萍. 浅析数学模型的构建方法及应用[J]. 青海师范大学学报: 自然科学版, 2011(3): 18-20.

[3] 李亚芹, 宗容, 李海燕. 以数学建模实践为平台的高等数学教学探索[J] . 高等教育研究, 2009, 26( 1) : 89-90.

[4] 徐兆棣, 李晓毅. 数学建模与数学实验的交互关系[J]. 沈阳师范大学学报: 自然科学版, 2010, 28(3): 350-352.

[5] 王茂芝, 郭科, 徐文皙, 等. 数学建模中的创新意识培养[J]. 大学数学, 2009, 25(1): 126-129.

Analysis and test of the solution to mathematical modeling

QU Xiao-hai, MEI Han-fei

(Department of Maths and Computing, Hunan University of Arts and Science, Changde 415000, China)

The application of mathematical modeling in reality, It is necessary to analyze the meaning of solution to judge appropriateness of the model. In order to further optimize model, In model analysis, several aspects are studied such as dimensional analysis, parameter sensitivity analysis, critical value analysis, hypothesis rationality analysis and error analysis. Model test is mainly concerned with practical feasibility, model refinement and perfection.

mathematical modeling; parameter sensitivity analysis; model refinement

10.3969/j.issn.1672-6146.2012.03.004

G 633.6

1672-6146(2012)03-0012-03

2012-09-12

湖南文理学院教改课题(JGYB0645)

曲孝海(1975-), 男, 讲师, 研究方向为智能优化. E-mail: xhqu1100@sina.com

(责任编校:刘刚毅)