一种任意构型双基合成孔径雷达成像算法

刘玉春 王 俊 高 博 刘保昌

（西安电子科技大学雷达信号处理国家重点实验室，陕西 西安 710071）

引 言

双基合成孔径雷达（SAR）指收发分置的SAR系统。由于其具有成本低、机动灵活、隐蔽性强等优点，近年来受到国内外研究人员的高度重视，对双基SAR成像模式［1－4］、性质分析［5－9］、二维谱分析［10－18］和成像算法［19－27］的研究逐渐深入。

双基SAR成像的时域处理方法性能优越，可应用于任意构型下，但是运算量很大，难以满足实时处理要求，现在一般采用频域处理方法。与单基SAR相比，双基SAR成像困难在于其收发双程斜距历程为双平方根项（DSR），无法直接使用驻相原理，导致二维参考频谱（下面简称二维谱）求解非常复杂。二维谱的求解是双基SAR成像算法的基础，其形式和精确性对成像算法有至关重要的影响。Loffeld双基公式（LBF）［10］对收发斜距历程在各自驻相点处进行二阶泰勒展开，利用驻相原理得到双基SAR点目标的二维近似频谱。其主要问题是未考虑收发平台的多普勒贡献率而简单地对收发相位历程进行平均截断。文献［11］、［12］对LBF算法进行了改进，分别应用时间带宽积（TBP）和瞬时多普勒贡献率对相位历程进行了加权处理，提高了二维谱的精确性。文献［13］在扩展LBF（ELBF）基础上根据欧几里德范数得到一个新的二维谱表示方法，考虑了收发相位历程的多普勒中心，因而更加精确。级数反演（MSR）算法［14］应用了级数反演原理，精度可以通过级数的阶数控制，聚焦性能优良，已经被广泛应用。文献［15］利用菲涅耳近似得到一种较为精确的二维谱求解算法，但是只能应用于小斜视角和小双基角。文献［16］在MSR基础上对斜距历程级数展开式的系数进行优化，得到了一种更为精确的二维频谱，但是其表达式较为复杂，增加了后续成像处理的复杂度。四阶精确传递函数（EETF4）二维谱近似解析算法［17－18］通过直接求解驻相点方程（一元三次方程）得到驻相点的解析解，进而得到较为精确的二维谱。

在上述二维谱求解算法的基础上，成像算法也相继出现。文献［19］提出基于LBF二维谱的逆尺度傅里叶变换（ISFT）双基SAR成像算法。文献［20］提出基于ELBF二维谱的平行等速构型双基线频调变标（CS）算法。文献［21］、［22］分别提出基于MSR二维谱［11］的方位不变构型双基距离多普勒（RD）和双基 OMEGA－K 成像算法。文献 ［23］［24］、［25］对接收机固定构型的双基SAR非线性CS（NLCS）算法进行了研究。文献［26］提出了基于MSR二维谱任意构型双基NLCS成像算法。文献［27］提出了基于平移不变构型的大斜视双基地SAR的二维可分离成像算法。

综上所述，为了能够得到具有较好聚集性能的任意构型双基SAR成像算法，首先要得到较为精确的二维谱，然后设计相应的成像算法或者借鉴适合的单基SAR成像算法。基于此思想，参考文献［17］、［18］，论文提出了一种基于EETF4二维谱的任意构型双基OMEGA－K成像算法。为了保证所求二维谱的精确性，首先把收发斜距历程泰勒四阶展开，通过直接求解驻相点方程得到驻相点的解析解，进而求得二维谱。由于二维谱表达式过于复杂，难以分解，所以很难应用RD、CS、NLCS等算法对其进行聚焦成像，所以采用了OMEGA－K算法对其进行处理。结合单基SAR的OMEGA－K成像算法思想，应用角度不变假设，通过处理二维谱，得到频率映射函数，推导出具有良好聚焦性能的任意构型双基OMEGA－K成像算法，并分析了角度不变假设的不变区域大小。

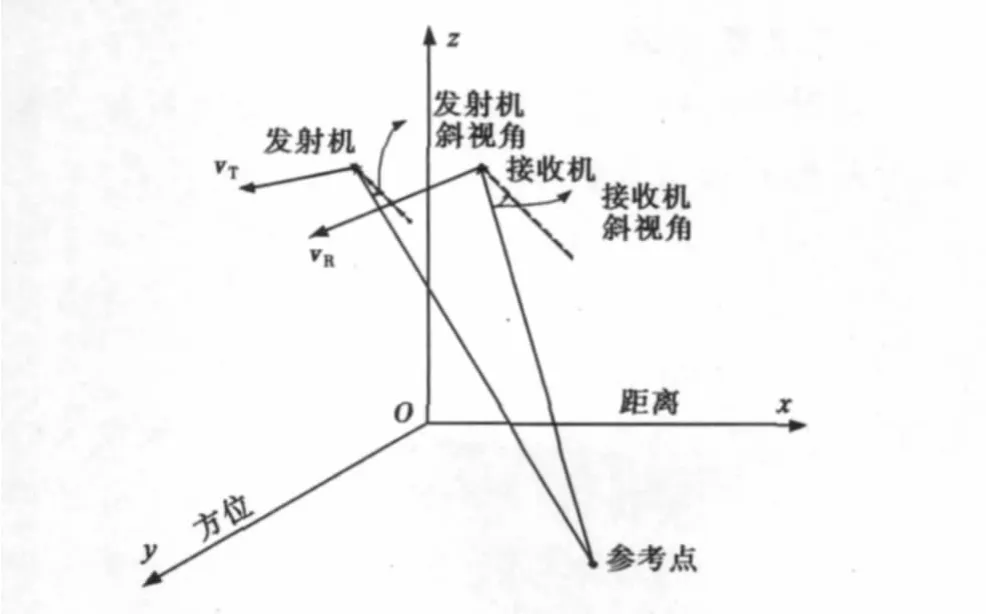
图1 双基SAR系统构型

1 双基SAR系统几何构型

任意构型的双基SAR几何模型如图1所示。假设收发平台都平行于地面运动，接收机运行速度为vR，以其速度方向为y轴正方向。发射机运动速度为vT，vR与vT夹角为α.参考点目标位于（x0，y0，0）.方位零时刻发射机位于（xT0，yT0，zT），接收机位于（xR0，yR0，zR）.方位t时刻收发平台到目标的斜距历程分别为

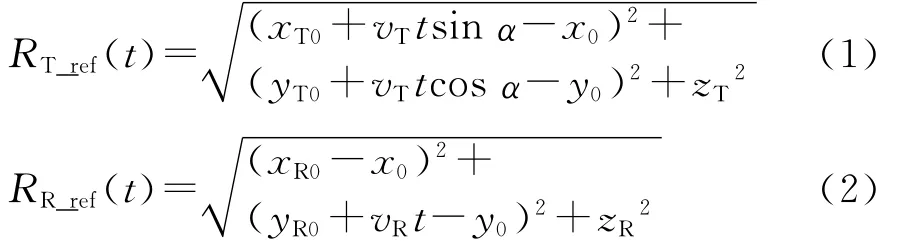
根据系统几何关系，方位零时刻收发平台的瞬时斜视角θsqT＿ref和θsqR＿ref为

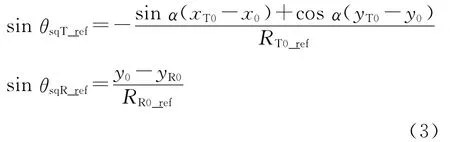
式中：RT0＿ref＝RT＿ref（0）；RR0＿ref＝RR＿ref（0）.收发双程的斜距历程为

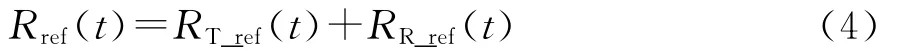
将式（4）泰勒四阶展开

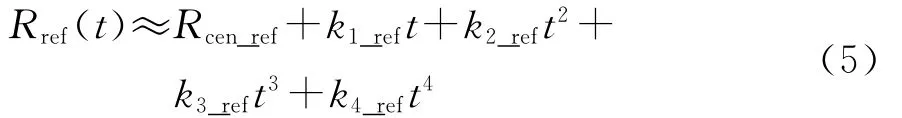
式中：

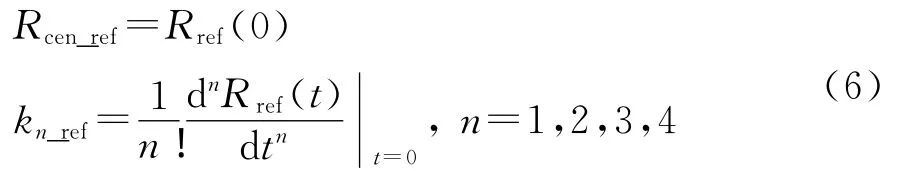
2 任意构型双基OMEGA－K成像算法

2.1 二维谱求解

假设发射机信号为chirp信号，则点目标回波信号解调后可以表达为

式中：wr（τ）为脉冲包络；wa（t）为由双基收发天线决定的方向图函数；kr为脉冲调频率。应用驻相原理对回波信号进行距离维（快时间）傅里叶变换可得

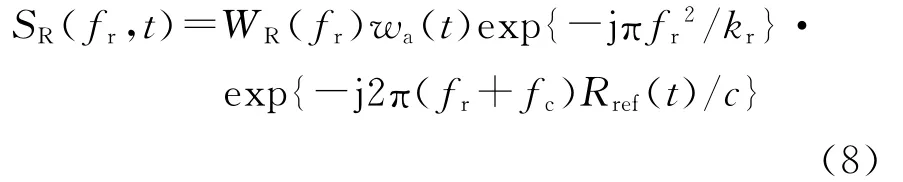
式中：fr为距离频率；WR（fr）＝wr（fr／kr）.二者仅是尺度变换。下面进行方位维（慢时间）傅里叶变换，可得

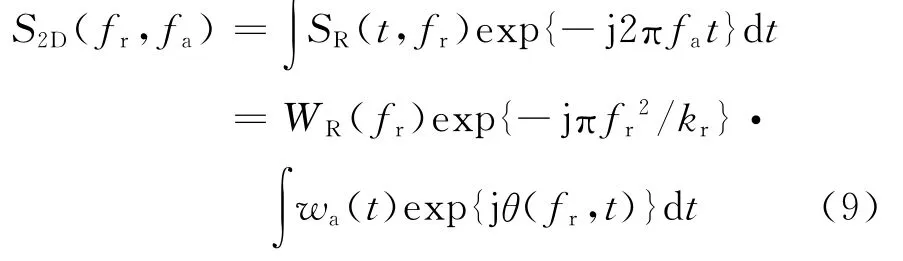
式中，fa为多普勒频率，θ（fr，t）为

对θ（fr，t）求导，可得

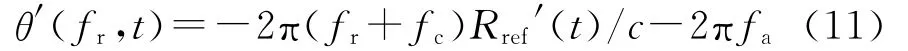
由驻相原理知，θ′（fr，t）＝0的解tref（驻相点）满足

结合式（5）和式（12），整理得

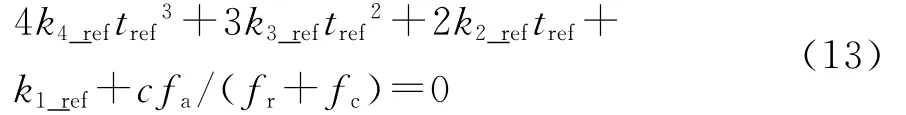
驻相点方程式（13）详细求解过程见文献［28］附录。把驻相点tref的解析解代入式（10）得到二维频谱的相位θ（fr，t）表达式

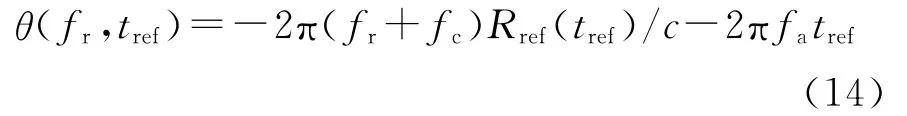
值得注意的是，式（14）中tref是关于fa和fr的函数。根据驻相原理，回波信号二维谱为

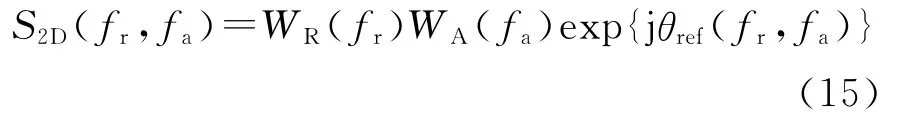
式中，WA（fa）＝wa（ttef）.相位θref（fr，fa）为

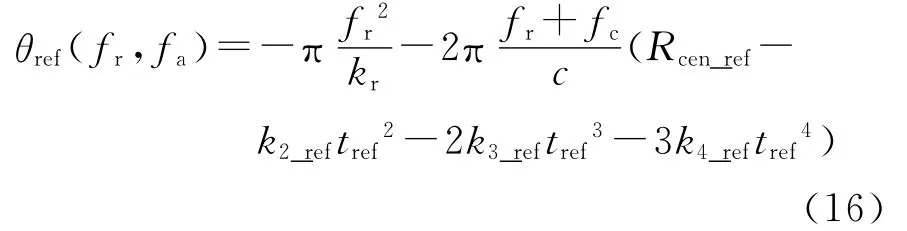
在求解二维谱的过程中，EETF4算法除了假设收发平台平行于地面运动外没有采用其他的假设，所以算法适用于任意构型的双基SAR成像系统。

2.2OMEGA－K成像算法研究

从式（16）可以看出，用EETF4得到的二维频谱较为复杂，难以分解，所以很难应用RD、CS、NLCS等算法对其进行聚焦成像，所以论文采用OMEGA－K成像算法。该算法具有不需要对频谱进行细致分解而只需要通过Stolt插值即可实现聚焦成像的优点。根据文献［29］，在推导距离频率映射函数时，二维谱相位要包含一个距离变量，并且此距离变量与二维谱的其他部分是分离的。为满足此要求，需要对二维谱式（16）做进一步处理。令ρ＝RT＿ref（0）／RR＿ref（0），ρ是一个由系统架构决定的量，式（6）的第二项等价于

式中：

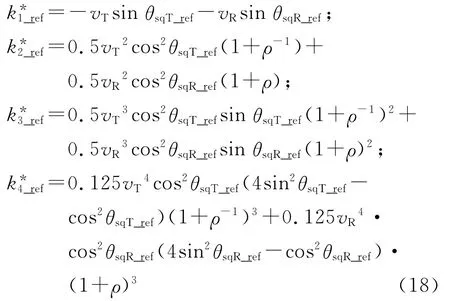
式中、均与Rcen＿ref无关而由双基系统架构决定。把式（17）代入式（13）中可以得到

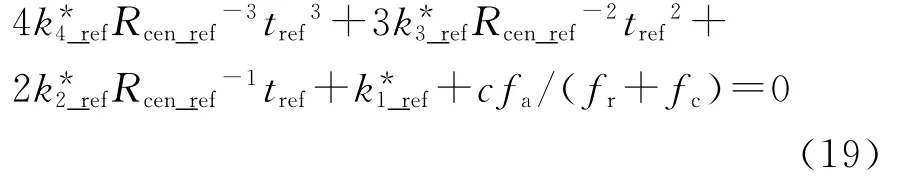
式（13）和式（19）等价。式（19）也可以写为

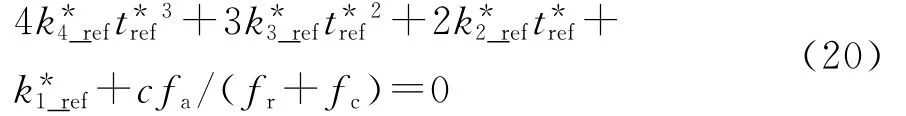
对比式（13）、式（19）和式（20），式（20）和式（13）的解之间有下面的关系：

由式（20）可知，t＊ref与Rcen＿ref无关。把式（21）代入式（16），可得

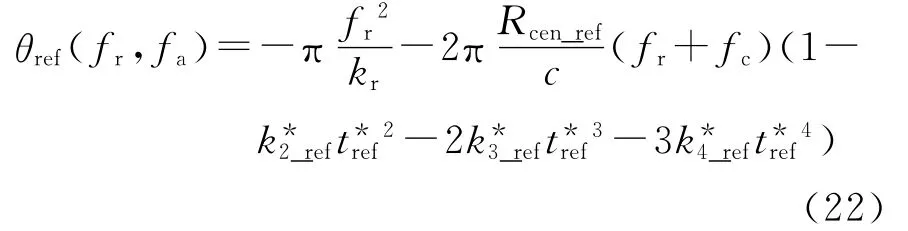
式（22）包含一个与其他部分分离的距离变量Rcen＿ref，满足了OMEGA－K算法对频谱相位的要求。

考虑成像场景中的另一个目标A，其二维谱为

SA＿2D（fr，fa）的相位为

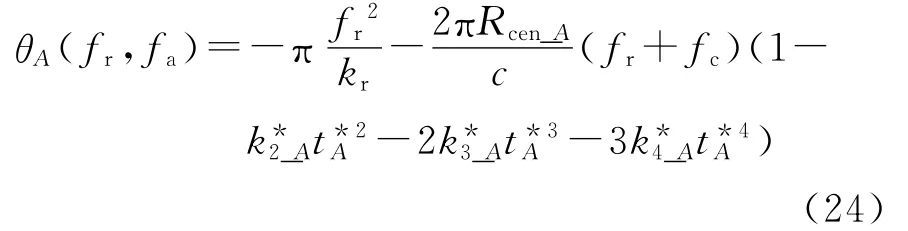
式 中Rcen＿A、、、、和Rcen＿ref、、、、、含 义 相 似。 为 了 应 用OMEGA－K成像算法，在此采取角度不变假设，即认为在一定区域 （此区域称为不变区域）的零方位时刻参考点和A点的收发瞬时斜视角和收发斜距比值（即ρ）的变化可以忽略不计，这样可以得到tA＊＝tr＊ef，式（22）和式（24）中括号内的项相同。

OMEGA－K算法的第一步是参考函数匹变为配滤波（RFM），经过 RFM 后SA＿2D（fr，fa）变为

令式（26）中括号内各项等于f′r＋fc，即可得到距离频率映射函数

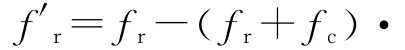
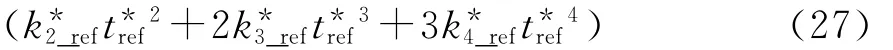
式中，f′r为频率映射后的距离频率。根据式（27），利用Stolt插值进行距离频率映射（fr→f′r）后，式（26）变为

进行二维傅里叶逆变换，就完成了对点目标A的聚焦成像。

综上所述，基于EETF4二维谱的OMEGA－K成像算法（下面简称为EETF4算法）流程如图2所示。

图2 OMEGA－K算法流程图

3 不变区域大小分析

EETF4算法的误差主要来源于两方面：一是角度不变假设，二是斜距历程展开误差。对于后者，由于本文把斜距历程进行了泰勒四阶展开，此误差已经非常微小，基本可以忽略不计（例如在下面的仿真中，k4＿ref＝－2.02×10－5m／s4，而斜距误差也在10－5m量级）。但是对大场景成像时，角度不变假设未必成立，所以必须对不变区域大小进行分析，以保证聚焦效果。由于高阶距离导数为快时间和慢时间的慢变函数，所以仅分析一阶和二阶距离导数的影响。参考点的一阶和二阶距离导数为

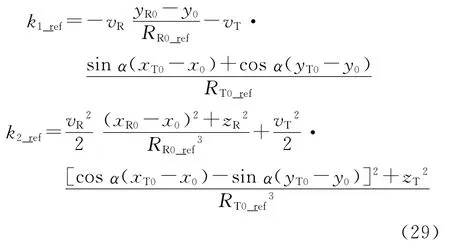
同理，假设点目标A相对于参考点的坐标为（δx，δy），不采用角度不变假设则有

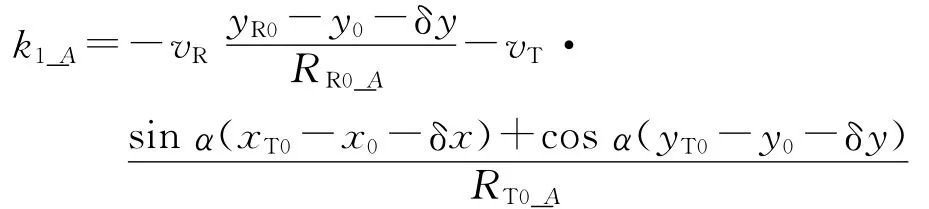
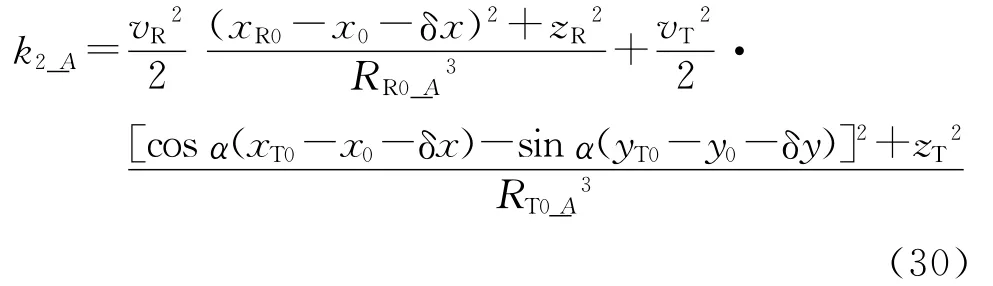
式中：

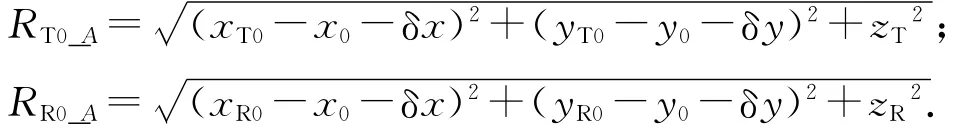
由文献［26］可知，不变区域大小主要受残余距离徙动（RCM）和二次相位误差（QPE）影响。对残余RCM，在此着重分析线形RCM（LRCM）和二次RCM（QRCM）。LRCM为

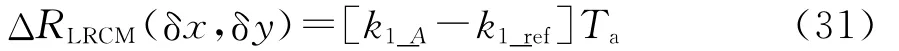
式中，Ta为合成孔径时间。QRCM为

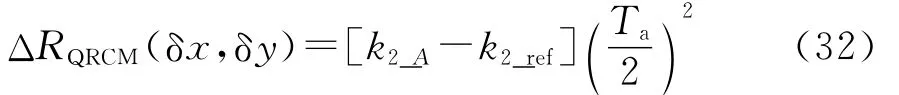
则总的RCM为

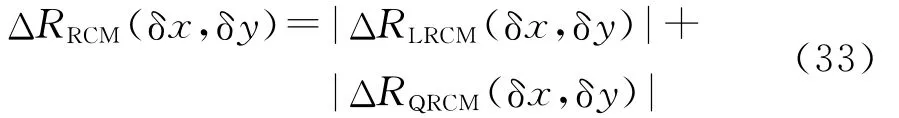
二次相位误差为

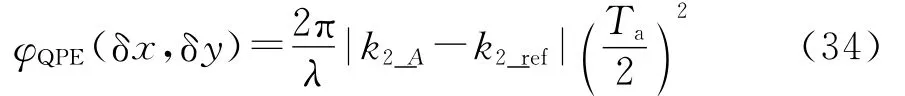
由此可得，距离不变区域大小为

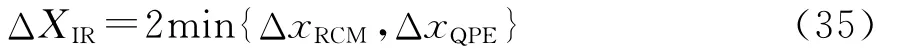
式中ΔxRCM和ΔxQPE分别由ΔRRCM（ΔxRCM，0）＜γRCMρr，φQPE（ΔxQPE，0）＜γQPEπ确定。

方位不变区域大小为

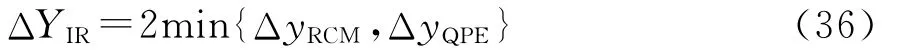
式中ΔyRCM和ΔxQPE分别由ΔRRCM（0，ΔxRCM）＜γRCMρr，φQPE（0，ΔxQPE）＜γQPEπ确定。式（35）和式（36）中：ρr为距离分辨单元；γRCM一般被设置为小于1的值；γQPE一般取小于0.5的值。

4 仿真及结果

根据上述算法对大斜视角、收发平台非平行运动任意构型机载双基SAR进行仿真，仿真参数如表1所示。对同一个场景中的三个散射点聚焦成像，取场景中心为坐标原点，三个点的坐标分别为：场景中心O（0，0），近距离点A（－200，0），远距离点B（400，0），单位为 m.仿真中采取EETF4算法和基于MSR二维谱的OMEGA－K算法［22］（下面简称为MSR算法）两种成像算法进行聚焦成像，通过对比成像结果来验证EETF4算法的聚焦性能。成像过程中两种算法均未作加窗处理。

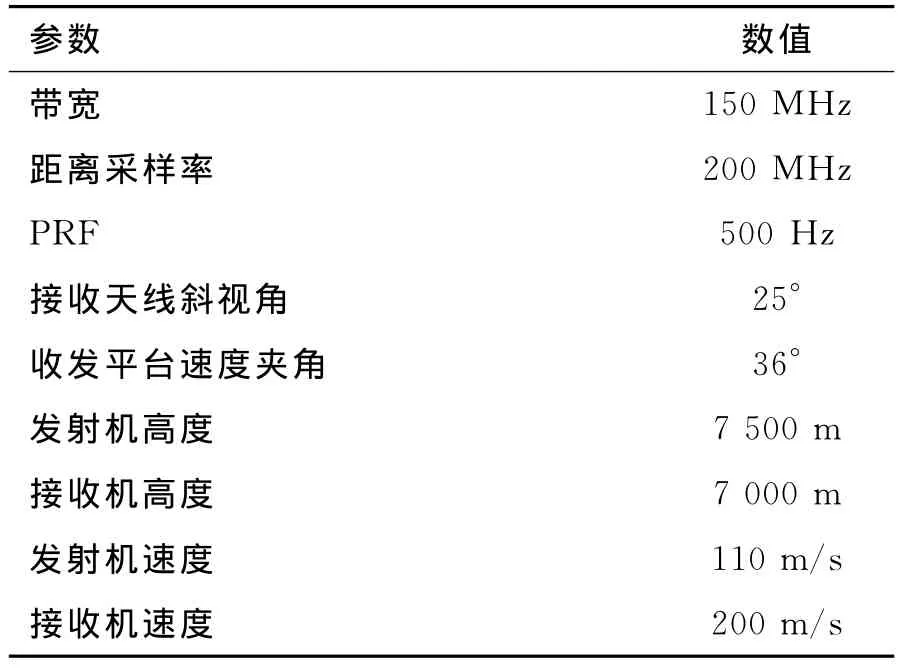
表1 实验参数设置

图3给出了两种算法的二维频谱误差的对比。从图3（a）、（b）可以看出，两种算法的最大误差分别为10－4和10－3rad量级，而在多普勒中心频率处误差更小。这些误差对成像影响非常小，故而两种算法都能够很好地对点目标进行聚焦成像。图3（c）（图像经过平滑处理）给出了两种算法误差比值图，二者比值呈“凹”字形分布，在对聚焦效果影响较小的多普勒中心附近，二者比值较为接近，而在对聚焦效果影响较大的部分，MSR算法的误差是EETF4算法的17～20倍。故而EETF4算法相比MSR算法误差更小，具有更好的聚焦性能。

图4给出了A点的成像结果（O点和B点结果与之相似，故而仅给出有代表性的A点成像结果）。三个散射点成像结果的方位向峰值旁瓣比（PSLR）、积分旁瓣比（ISLR）、脉冲响应宽度（IRW）等聚焦性能参数如表2所示。

从图4和表2可以看出，两种算法均能够对仿真中比较极端的双基构型进行良好聚焦，其聚焦性能非常接近，对同一个散射点而言，两种算法的聚焦结果无法从其轮廓图或方位向剖面图中看出区别。

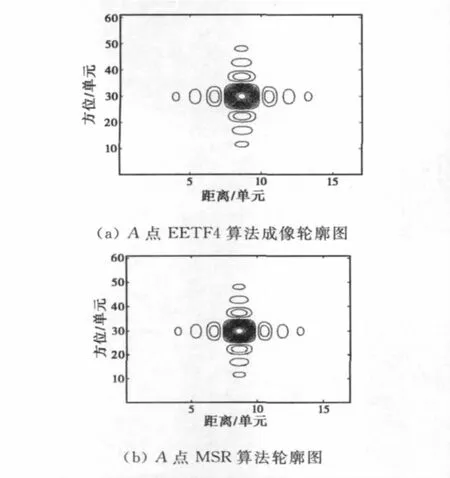
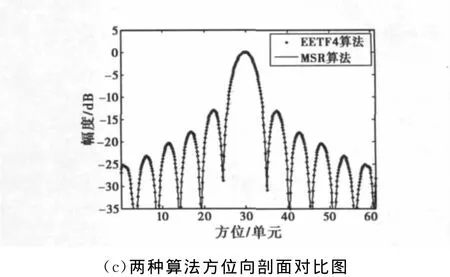
图4 两种算法的成像结果

表2中的聚焦参数也为上述观点提供了数据支持。从表2可以看到，这两种算法仿真聚焦结果的IRW均相同，而PSLR和ISLR的差异也仅仅是10－4dB量级，二者的聚焦性能几乎完全相同。对于场景中心O和近距离点A而言，EETF4算法的聚焦性能略好于MSR算法，这是因为在求解二维谱时，EETF4算法通过求解驻相点方程得到驻相点的解析解，而MSR算法采用级数反演技术，得到的仅是驻相点较为精确的估计而非解析解，故而EETF4算法的二维谱更精确。又因为都对斜距历程高阶泰勒展开，二者相距甚微。但在远距离点B，EETF4算法的PSLR要比MSR算法略低，这表明与MSR算法相比，EETF4算法对距离更敏感一些。此外，两种算法都用到了角度不变假设，在成像场景中忽略了参数的空变性，所以从表2中可以看到，随着距离的增加，两种算法的聚焦性能逐渐下降。因此，对于大场景成像情况，需要考虑参数空变性，应该根据不变区域大小对成像数据进行分块处理。

表2 两种算法的聚焦参数对比

5 结 论

论文提出了一种基于EETF4的双基OMEGA－K成像算法。该算法首先把收发斜距历程进行泰勒四阶展开，直接求解驻相点方程得到驻相点的解析解，进而求得较为精确的二维谱。然后结合单基SAR的OMEGA－K成像算法思想，通过处理二维谱，使之转化为相位包含一个距离变量并且此距离变量与其他部分分离的形式，得到频率映射函数，推导出适用于任意构型双基OMEGA－K成像算法。仿真实验表明算法具有良好的聚焦性能，能够应用于较为极端的双基构型。在算法中使用了角度不变假设并分析了不变区域大小，对于较大场景成像需要考虑参数的空变性，进行分块处理。

［1］ZHEN Jie，ZHANG Zhenhua，WU Shunjun，et al.GNSS illuminator based high range resolution algorithm in space－surface bistatic SAR ［C］／／IGARSS.Honolulu，25－30July，2010：4608－4611.

［2］WANG Wenqin.GPS－based time ＆ phase synchronization processing for distributed SAR［J］.IEEE Trans Aerosp Electron Syst，2009，45（3）：1040－1051.

［3］徐 丰，金亚秋.复杂自然场景双站SAR成像模拟［J］.电波科学学报，2008，23（6）：1022－1031.

XU Feng，JIN Yaqiu.Bistatic SAR imaging simulation［J］.Chinese Journal of Radio Science，2008，23（6）：1022－1031.（in Chinese）

［4］LI Wenchao，HUANG Yulin，YANG Jianyu，et al.An improved radon－transform－based scheme of Doppler centroid estimation for bistatic forward－looking SAR［J］.IEEE Geosci Remote Sens Lett，2011，8（2）：379－383.

［5］戴征坚，谭 昕，许建平.双基地雷达的主要性能分析与实验方法研究［J］.电波科学学报，2011，26（5）：951－955.

DAI Zhengjian，TAN Xin，XU Jianping.Main performance analysis and experiment method research of bistatic radar［J］.Chinese Journal of Radio Science，2011，26（5）：951－955.（in Chinese）

［6］武拥军，黄 冶，吴先良.机载双站聚束合成孔径雷达的三维空间分辨特性［J］.电波科学学报，2011，26（6）：1200－1206.

WU Yongjun，HUANG Ye，WU Xianliang.Threedimensional spatial resolution of airborne bistatic spotlight SAR［J］.Chinese Journal of Radio Science，2011，26（6）：1200－1206.（in Chinese）

［7］朱振波，汤子跃，张亚标，等.基于Radon变换的双站SAR多普勒参数估计［J］.电子与信息学报，2008，30（8）：1331－1334.

ZHU Zhenbo，TANG Ziyue，ZHANG Yabiao，et al.The estimation of Doppler parameter of bistatic SAR based on radon translation［J］.Journal of Electronics ＆Information Technology，2008，30（8）：1331－1334.（in Chinese）

［8］LIU Zhe，YANG Jianyu，ZHANG Xiaoling，et al.Study on spaceborne／airborne hybrid bistatic SAR image formation in frequency domain［J］.IEEE Geosci Remote Sens Lett，2008，5（4）：578－582.

［9］黄钰林，杨建宇，武俊杰，等.机载双站SAR分辨率特性分析［J］.电波科学学报，2008，23（2）：174－178.

HUANG Yulin，YANG Jianyu，WU Junjie，et al.Resolution characteristic analysis for bistatic airborne SAR［J］.Chinese Journal of Radio Science，2008，23（2）：174－178.（in Chinese）

［10］LOFFELD O，NIES H，PETERS V，et al.Models and useful relations for bistatic SAR processing［J］.IEEE Geosci Remote Sens Lett，2004，42（10）：2031－2038.

［11］WANG R，LOFFELD O，NIES H，et al.Bistatic point target reference spectrum in the presence of trajectory deviations［J］.IET Radar Sonar Navig，2009，3（2）：177－185.

［12］YANG Kefeng，HE Feng，LIANG Diannong，et al.A two－dimensional spectrum for general bistatic SAR processing［J］.IEEE Geosci Remote Sens Lett，2010，7（7）：108－112.

［13］WANG R，LOFFELD O，NEO Y，et al.Extending Loffeld＇s bistatic formula for the general bistatic SAR configuration［J］.IET Radar Sonar Navigation，2010，4（1）：74－84.

［14］NEO Y，WONG F，CUMMING I.A two－dimensional spectrum for bistatic SAR processing using series reversion［J］.IEEE Geosci Remote Sens Lett，2007，4（1）：93－96.

［15］GENG Xupu，YAN Honghui，WANG Yanfei.A two－dimensional spectrum model for general bistatic SAR［J］.IEEE Trans Geosci Remote Sens，2008，46（8）：2216－2223.

［16］WANG Fang，LI Xiang.A new method of deriving spectrum for bistatic SAR processing ［J］.IEEE Geosci Remote Sens Lett，2010，7（3）：483－486.

［17］ZHONG Hua，LIU Xingzhao.A fourth－order imaging algorithm for spaceborne bistatic SAR ［C］／／IGARSS.Denver，2006：1196－1199.

［18］ELDHUSET K.Spaceborne bistatic SAR processing using the EETF4algorithm［J］.IEEE Geosci Remote Sens Lett，2009，6（2）：194－198.

［19］NATROSHVILI K，LOFFELD O，NIES H，et al.Focusing of general bistatic SAR configuration data with 2－D inversescaled FFT［J］.IEEE Trans Geosci Remote Sens，2006，44（10）：2718－2727.

［20］WANG R，LOFFELD O，NIES H，et al.Chirp scaling algorithm for the bistatic SAR data in the constantoffset configuration［J］.IEEE Trans Geosci Remote Sens，2009，47（3）：952－963.

［21］NEO Y，WONG F，CUMMING I.Processing of azimuth－invariant bistatic SAR data using the range doppler algorithm［J］.IEEE Trans Geosci Remote Sens，2008，46（1）：14－21.

［22］LIU Baochang，WANG Tong，WU Qisong，et al.Bistatic SAR data focusing using an Omega－K algorithm based on method of series reversion［J］.IEEE Trans Geosci Remote Sens，2009，47 （8）：2899－2912.

［23］QIU Xiaolan，HU Donghui，DING Chibiao.An improved NLCS algorithm with capability analysis for one－stationary BiSAR［J］.IEEE Trans Geosci Remote Sens，2008，46（10）：3719－3186.

［24］陈晓龙，丁赤飚，梁兴东，等.改进的接收机固定双站NLCS成像算法［J］.电子与信息学报，2008，30（5）：1041－1046.

CHEN Xiaolong，DING Chibiao，LIANG Xing dong，et al.An improved NLCS imaging algorithm of bistatic SAR with a stationary receiver［J］.Journal of Electronics ＆ Information Technology，2008，30（5）：1041－1046.（in Chinese）

［25］BAI Xia，SUN Jinping，MAO Shiyi.A novel approach for bistatic SAR imaging using a stationary receiver［C］／／ICSP2008Proceedings.Beijing，26－29 October，2008：2250－2253.

［26］WONG F，CUMMING I，NEO Y.Focusing bistatic SAR data using the nonlinear chirp scaling algorithm［J］.IEEE Trans Geosci Remote Sens，2008，46（9）：2493－2505.

［27］蔡复青，何 友，宋 杰.大斜视双基地SAR的二维可分离成像算法［J］.数据采集与处理，2010，25（5）：554－559.

CAI Fuqing，HE You，SONG Jie.Two－dimentional separated approach for high squint bistatic SAR imaging［J］.Journal of Date Acquisition ＆ Processing，2010，25（5）：554－559.（in Chinese）

［28］ELDHUSET K.A new Fourth－Order processing algorithm for spaceborne SAR［J］.IEEE Trans Aerosp Electron Syst，1998，34（3）：824－835.

［29］CUMMING G，WONG F H.Digital Processing of Synthetic Aperture Radar Data：Algorithms and Implementation［M］.Norwood：Artech House，2005：323－367.