串联系统的备件配置方法
2012-06-03冯玉姣
冯玉姣
(中船重工第七一〇研究所,湖北 宜昌 443000)
0 引言
当前,准确、有效地预测装备全系统、全寿命期间的备件需求问题是装备综合保障中的研究热点之一,国内外有关学者对此展开了大量的研究。针对单不可修部件来说,在可靠性信息已知的前提下,建立了各种寿命分布类型备件的保障度与需求量模型,能够较为准确地预测全寿命期间的备件需求[1-3],这些模型在工程中已经得到了广泛的应用。然而,对于由多个不可修部件或者采用换件维修方式的系统而言,不仅需要预测各部件的备件需求量,还要考虑或权衡在有限的经费条件下,各备件如何进行合理的配置以达到较高的系统保障度,该问题仍然没有得到很好的解决。
针对相同寿命分布类型不可修部件组成的串联系统,除指数分布外,其它几种典型分布如威布尔分布、正态分布等的备件预测模型较为复杂,导致在部件数目较多的情况下,模型的建立与求解过程都比较复杂,求解困难。为方便计算,经典的方法是在任务时间小于部件平均寿命时,假设每个部件任务期间最多只发生一次或两次故障,然后采用状态枚举和概率统计的方法推导得出备件需求量的解析表达式,从而得到近似的结果[1,4],虽然结果与实际较为接近,但不能进行全寿命的备件预测,具有很大的局限性。
针对不同寿命分布类型不可修部件组成的串联系统,目前工程中主要采用的是国军标GJB 4355《备件供应规划要求》中推荐的方法——单项法[5],直接对各零部件提出保障度要求(一般要求每项备件的保障度范围在0.80~0.99之间),分别进行备件预测,该方法实施简单,可操作性强,但是不能从系统整体角度控制备件数量和保障度的关系,容易造成备件过量储存,导致全寿命费用增大。因此,大量的文献提出了各种系统优化的配置方法,即根据装备的战备完好性或任务可靠度等要求,以保障费用为约束条件而建立相应的备件配置模型,然后采用各种优化算法如边际效益、动态规划或遗传算法等得到最优的配置方案。如丁定浩结合实际的情况,分别考虑备件的费用、体积和质量等综合因素,提出了系统保障度分配模型,并采用动态规划的优化方法得到备件的配置方案[6];程海龙等建立了系统满足率约束下的备件模型,采用边际效益方法进行优化[7]。然而,这类方法大多只适用于指数分布的各类系统,无法应用于非指数分布组成的系统。主要原因也是由于非指数分布并不具有指数分布的 “无记忆性”,其备件保障度解析模型的建立是比较困难的。目前主要采用的是Monte-Carlo模拟方法,通过计算机产生随机数来模拟每个非指数分布部件的实际使用过程,根据大数定律,采用概率统计和线性插值的方法求出备件需求量,进而与各种优化算法相结合得出备件配置方案[8]。然而在备件种类较多时,比如100种,假设每个零部件最多配置2个备件,也有3100种组合,每种组合进行10000次仿真,其计算量也是比较大的,效率低,更不利于工程化;该方法常常只用来对解析法得到的配置方案进行仿真验证。
针对串联系统的备件配置问题,首先根据指数分布的良好特性,建立由指数分布部件构成的串联系统的备件需求预测和配置模型;然后根据累积失效相等原则,将非指数分布等效成指数分布,进而利用指数分布串联系统的备件模型近似计算几种典型非指数部件串联系统的备件需求量,最后通过Monte-Carlo模拟方法验证结果的有效性。
1 指数分布部件串联系统的备件模型
1.1 部件寿命服从相同指数分布的情况
若某串联系统由m个相同的不可修部件组成,且部件寿命服从失效率为λ的指数分布。在保障度要求为α,且备件存放期内无失效的情况下,通过下面公式计算得到在时间(0,T]内的故障次数,也即备件需求量[9]:

进一步可化简为:
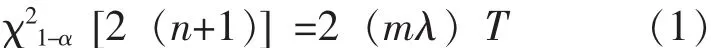
利用上述公式能够计算出备件的需求量,工程中还可以直接通过查表获得,这是比较方便的。
1.2 部件寿命服从不同指数分布的情况
若系统由m个不相同的不可修部件串联组成,不可修部件寿命服从失效率为λi(i=1,2,…,m)的指数分布,各部件费用为ci。常见的系统备件配置模型主要有以下两种:
a)以系统保障度α为目标函数,以总费用C为约束条件,寻求最优的配置,使得在费用限制下达到的保障度最大,数学模型为:
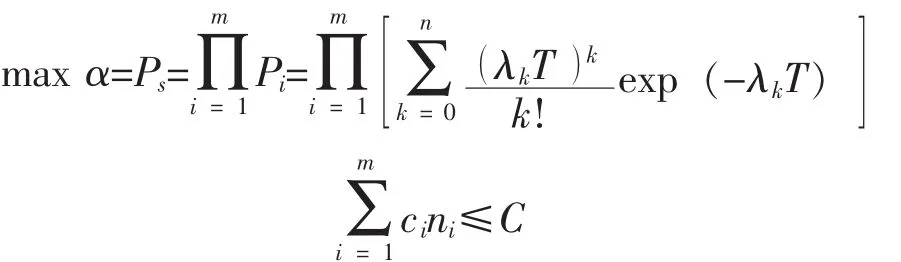
b)以总费用C为目标函数,系统保障度α为约束条件,寻求最优的备件配置,使得在保障度约束下,总费用最小,数学模型为:
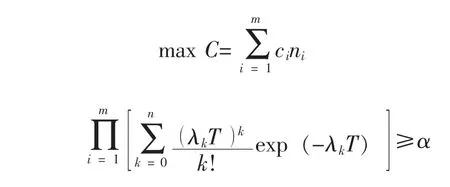
在此基础上,利用动态规划、边际效益或遗传算法等方法进行优化,得到最终的配置结果。各种优化算法的实现过程见文献 [6-7],在此不详细叙述。
2 非指数分布的指数等效方法
由于指数分布 “无记忆性”的性质,当前很多学者都是以指数分布为基础开展备件配置研究的[10-11]。而当组成系统的某个或某些部件服从非指数分布时,建立备件保障度的解析模型和求解时是十分困难的。然而,如果找出非指数分布与指数分布间的联系和差异,利用指数分布进行近似计算就将为工程应用带来极大的方便。
刻画一种分布的基本参数包括平均寿命、失效率及可靠度等。已有的文献研究表明,在平均寿命相等的情况下,指数分布类型部件的故障次数(或备件数量)要比非指数分布的多,即具有保守性;并且常常是过于保守,那么如果将非指数分布看作与其平均寿命相等的指数分布,利用指数分布的备件模型进行近似计算,结果自然就会造成资源浪费[12]。因此,本文从失效率的角度,建立非指数分布与指数分布间的关系。


其中,λ为常数。对于其它分布的情况,利用上式则可等效成失效率为常数的指数分布,表明两种分布在相同时间内的平均累积故障次数相等。然而,随着时间T的增长,这种等效的误差会越来越大。因此,本文只在平均寿命以内进行等效。具体的等效方法为:

3 非指数类部件串联系统的备件配置方法及实例分析
3.1 相同非指数类部件串联系统
针对由多个相同不可修部件组成的串联系统在给定保障度下备件数量的确定,经典的方法是在单不可修备件需求模型的基础上直接利用系统与单元保障度间的关系得到,即:
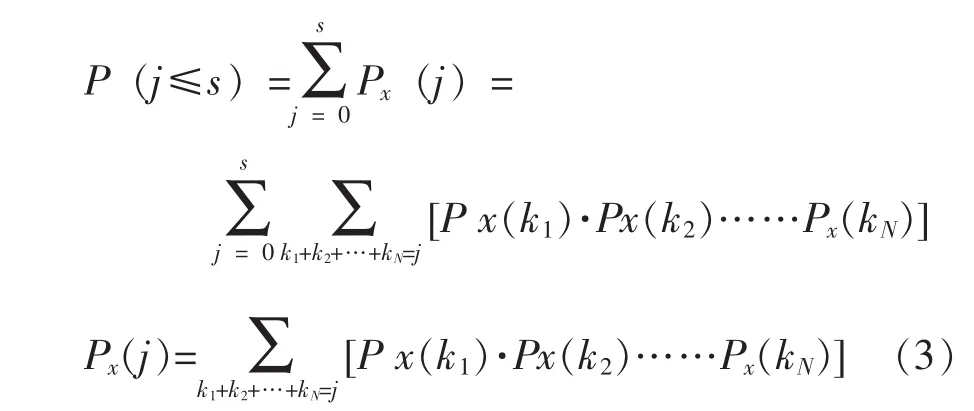
然而,在服从具体分布的时候,除指数分布外,其它分布利用式(3)计算是比较困难的,需要预设一定的假设条件。
3.1.1 服从 Weibull分布的部件




然后代入式(1)得到:
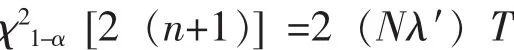
通过查表即可得到备件数量。下面通过实例,将经典的方法、本文方法以及模拟方法的结果进行比较。如表1所示。
从表1可以看出,经典方法的结果由于假设每个部件最多只发生一次故障,导致计算结果比真实结果偏小,随着时间的延长,误差越来越大,容易造成备件短缺,且对于任务时间大于平均寿命时没有给出计算公式;而近似方法则比模拟结果稍微偏大,但并不过大,在误差允许范围内,并且当时间大于平均寿命时,与模拟结果吻合得较好。

表1 N=5, λ=0.7854, β=2.0, μ=1, α=0.9。
3.1.2 服从正态分布的部件
以正态分布为例,研究由N个同种不可修部件串联,部件的寿命服从正态分布N(μ,σ2),总工作时间为T,保障度为α时的备件数量。同样,经典方法结果为:
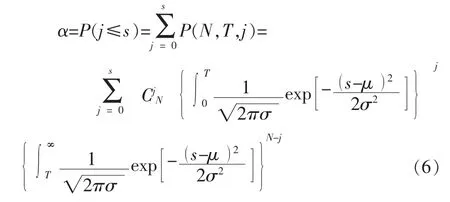
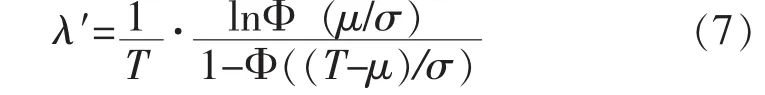
然后代入式(1)得到结果。表2给出了3种方法的结果。

表2 N=5,μ=10,σ=2,α=0.9。
从表2可以得出与表1相同的结论,即经典方法比实际结果略微小,而本文的近似方法结果偏保守,不过于保守。实际上,备件配置偏多显然比备件短缺要好。
3.1.3 服从 Gamma 分布的部件
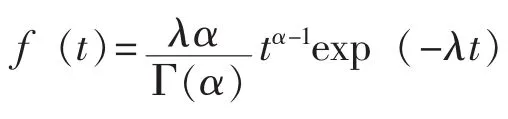
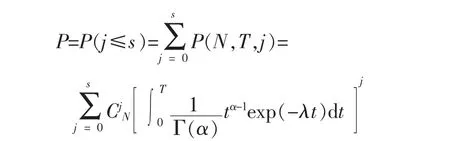
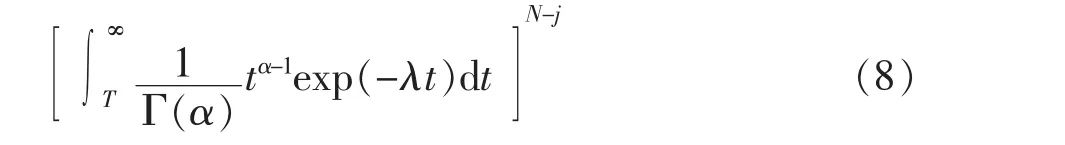
而根据等效的方法,先将Gamma分布失效率转化成指数分布,即

然后代入式(1)得到结果。表3给出了3种方法的结果。
结果表明:本文的等效方法在计算结果的精确度以及计算过程的简便性上都要比经典方法优些。

表3 N=5,μ=10,λ=0.2,σ=2,α=0.9。
3.2 不同非指数部件串联系统
对于由不同寿命分布部件组成的串联系统,建立其备件配置的解析模型和求解是比较困难的,当前主要依靠模拟仿真和边际效益相结合的方法[7]。而根据前面的研究,利用指数等效方法,将每个单部件等效成指数分布,进而预测备件的需求是比较准确和方便的。因此,不同寿命分布的部件串联系统可以先转化为多个指数分布部件串联的情况,然后采用1.2节的方法就能够确定各分部件的备件数量。以下给出一个具体的实例。系统中部件参数如表4所示。要求系统在工作时间为1200h内的保障度达到0.9。采用近似方法等效和边际效益方法优化后,得到各部件的备件数量如表4所示。总费用为45.1万元,系统保障度为0.9025。
进一步,为验证表中配置结果的有效性,利用Monte-Carlo方法进行仿真验证,得到如图1所示的备件保障度与费用曲线图,各分部件的保障度如图2所示。其中,图中的 “o”表示模拟得到的保障度, “*”表示解析法得到的近似保障度。
从图1和2可以看出,利用本文近似方法得到系统的备件配置结果,会比实际要求的保障度略高。例如本文按照0.90的保障度要求进行配置,得到的方案理论值为0.9025,而实际能达到0.9307。原因有两点:1)备件的数量只能是整数而非小数,因此在优化过程中,每次只能增加的备件个数为1,造成保障度的增加不是连续的;2)近似算法本身造成的误差,从图2可以看出每个分部件的模拟保障比解析保障度要高,因此低估了保障度就容易造成每个部件出现多配备件。根据该方法得到的结果虽然不是最优的结果,但是离最优的结果已经比较接近,略微保守,误差是可接受的,能够满足工程上的要求,而且实施简便,可操作性强。


表4 系统各部件相关数据及配置结果
4 结束语
在备件的保障问题中,很多问题只有通过近似的方法或者预设假设条件才能求出接近实际问题的近似解。针对不可修部件串联系统的备件配置问题,建立了指数分布串联系统的备件需求预测模型,以及利用指数分布串联系统的备件模型近似计算非指数部件串联系统的备件需求量,其结果与经典方法及Monte-Carlo模拟方法的结果是一致的。该方法具有精度高、简单可操作性强的优点,能够为工程应用带来方便。利用近似的方法也为复杂系统的备件配置以及全寿命期间的备件需求预测问题提供了研究思路。
[1]张建军,李树芳,张涛,等.备件保障度评估与备件需求量研究 [J].电子产品可靠性与环境试验,2004,22(6): 18-22.
[2]李金国,丁红兵.备件需求量计算模型分析 [J].电子产品可靠性与环境试验,2000,18(6):11-14.
[3]陈凤腾,左洪福.基于贝叶斯的航空备件需求研究与应用 [J].中国民航大学学报,2011,29(2):13-17.
[4]张涛.装备使用阶段维修保障能力评估建模与分析 [D].长沙:国防科学技术大学,2004.
[5]蔡泽明,康锐,龙军.面向系统优化的备件动态配置方法 [J].系统工程与电子技术,2010,32(11):2363-2366.
[6]丁定浩.备件保障性的综合与分配模型 [J].电子产品可靠性与环境试验,2006,24(2):1-6.
[7]程海龙,康锐,肖波平,等.备件满足率下的备件模型.系统给出与电子技术 [J].系统工程与电子技术,2007, 29(8): 1314-1315.
[8]龙军,康锐,马麟,等.任意寿命分布的多部件系统备件配置优化算法 [J].北京航空航天大学学报,2007, 33(6): 698-700.
[9]程文鑫,秦健,张志华.基于可靠性增长的备件需求模型及其统计分析 [J].北京理工大学学报,2008,28(3): 230-232.
[10]程海龙,康锐,肖波平,等.备件满足率下的备件模型[J].系统工程与电子技术,2007,29(8):1314-1316.
[11]张涛,高大化,郭波,等.多阶段任务系统的备件保障度模型研究 [J].系统工程学报,2006,21(1):86-91.
[12]刘天华,张志华,程文鑫.Weibull型备件需求量确定方法研究 [J].海军工程大学学报,2010,22(6):101-106.
[13]金星,文明,李俊美.寿命服从指数分布产品相关失效解析分析 [J].装备指挥技术学报,2002,13(4):37-39.
