广义向量拟似变分不等式的通有稳定性和本质连通区

李盛强

(重庆大学数学与统计学院，重庆 401331)

本质区在稳定性的研究中是一个重要的工具。1950年，Fort［1］首先提出从紧度量空间映射到自身的一个连续映射的本质不动点的概念，并且证明了任意的映射都可以大致接近于一个不动点都是本质的映射。由于即使是恒同映射也不一定存在本质不动点，1952年Kinoshita［2］提出了不动点集本质区的概念，并且证明了从Hilbert空间映射到自身的任意连续映射都至少存在一个不动点集的本质区。受到以上研究成果的启发，Wu和Jiang［3］引入了有限博弈的本质Nash均衡点的概念，并证明了任意的有限博弈大致接近于Nash均衡点是本质的博弈。之后，Jiang［4］引入了Nash均衡点集本质区的概念，并且证明了每个有限博弈都存在至少1个Nash均衡点集的本质区。1986年Kohlberg和Mertens［5］提出对于有限博弈，一个较为满意的解的概念应该称为Nash均衡点集的本质区，并且证明对于任何有限博弈都存在Nash均衡点集的有限区，其中至少1个区是本质的。1990年Hillas［6］提出了从另一种方法研究稳定性，这与传统的从Nash均衡点的扰动问题研究稳定性不同。近些年来，Yu、Yang、Luo、Xiang、Isac、Lin等将本质区的概念引入各种非线性问题中，如Ky Fan问题、均衡问题、变分不等式问题以及向量优化问题等。

近些年来，变分不等式的理论是研究非线性分析的一个重要方向。1980年以来，关于广义向量拟似变分不等式解的存在性已经有相当多的研究成果，但是广义拟似变分不等式的解不一定唯一，所以该问题的稳定性研究就显得很重要。传统研究稳定性的方法是对问题进行参数扰动后求解集对参数的各种连续性结果，即研究解集映射S(p)的连续性。1999年，俞建［7］利用Fort、吴文俊与江嘉禾所提出了本质解的概念与Mertens提出的本质连通分支的概念，研究了拟变分不等式的解集的稳定性，证明了这类拟变分不等式的解集具有通有稳定性且本质连通区是存在的。罗群、邓晓红［8］研究了广义向量似变分不等式解集的通有稳定性。2007年，陈建尘、龚循华［9］提出了广义拟变分不等式解集的稳定性及本质连通区的存在性。本文综合了近些年来在变分不等式通有稳定性及本质连通区方面的研究方法，研究了更为广泛的广义向量拟似变分不等式问题的通有稳定性及本质连通区，并且更进一步地研究了本质连通区的稳定性。

1 预备知识及定义

广义向量拟似变分不等式(GVQVLI):设E是Banach空间，X、Y是2个Hausdorff拓扑线性空间，K是X的非空闭凸子集，T:K→2L(E，Y)，S:K→2K，η:K×K→E，寻找，使得对任意的，存在，满足

定义1 称Q⊂X是X中的一个剩余集，若Q包含一列X中稠密开集的交。

引理1 考虑GVQVLI(S，T，η)问题，假设满足条件:① S是K上连续紧凸值映射，且对任意x∈K有intS(x)≠∅;②T在K上是上半连续紧凸值映射;③ η(·，·)在K×K上是连续的;④ 固定x∈K，η(·，x)是仿射的;⑤ 对于任意x∈K，如果x∈intG(x)，则η(x，x)=0。则广义向量拟似变分不等式有解。

引理2 设X是度量空间，A，An∈K(X)满足对任意的O⊃A，存在自然数N，使得对任意的n＞N，都有An⊂O，则任一满足xn∈An的序列 { xn}必有聚点x*∈A。

备注1 设(X，d)为度量空间，记K(X)表示X的所有非空紧子集全体，CK(X)表示X的所有非空紧凸集全体。空间 K(X)和 CK(X)的拓扑由 Hausdorff度量 h产生，h定义如下:h(C，D)=，其中

引理3 设(X，d)为度量空间，h表示由d诱导的Hausdorff度量，则(CK(X)，h)在(K(X)，h)中闭。

2 广义向量拟似变分不等式的通有稳定性

令 E、X、Y、S、T 和 η 的定义不变，设

对任意的 u1=(S1，T1，η1)，u2=(S2，T2，η2)∈M，定义

其中 h1、h2是 CK(K)和 CK(L(E，Y))上的 Hausdorff度量。

定理1(M，ρ)是完备度量空间。

证明(M，ρ)是度量空间，显然成立，只需证(M，ρ)是完备的。

设 {un=(Sn，Tn，ηn)}是 M 中的 Cauchy列，则∀ε ＞0，∃N，使得对于∀n，m ＞N 有 ρ(un，um)＜ ε，从而∀x，y∈K，都有 h1(Sn(x)，Sm(x))＜ ε，h2(Tn(x)，Tm(x))＜ ε，‖ηn(x，y)－ ηm(x，y)‖ ＜ ε。由于{ Sn(x)}是CK(K)中的Cauchy列，{ Tn(x)}是CK(L(E，Y))中Cauchy列，(E，‖·‖)是Banach空间，由引理3 知，存在 S(x)∈CK(K)，T(x)∈CK(L(E，Y))，η(x，y)∈X，使得

下面证 T 是上半连续的，S 是连续的，η(·，·)是连续且 η(·，x)是仿射的，η(x，x)=0。

1)∀x0∈K。要证T(x0)是下半连续的，只需证对于∀x0的邻域U，∀x∈U，∃T(x0)邻域O，使得T(x)⊂O。由于 ∃ε0＞ 0，所以 {ξ:d(ξ，T(x0))＜ε0}⊂O。下证 T(x)⊂ {ξ:d(ξ，T(x0))＜ε0}。令，其 中又且由于Tn→T，故 h2(Tn(x)，T(x))≤ε0/3，h2(Tn(x0)，T(x0))≤ε0/3，而由 Tn的下半连续性有，所以

故 T(x)⊂ {ξ:d(ξ，T(x0))＜ε0}⊂O，即T(x)在K上是上半连续的。

2)要证 S在 K上是连续的，只需证∀x0∈K，∀ε＞0，∃x0的邻域 N(x0)使得∀x∈N(x0)有h1(S(x)，S(x0))＜ε。由于对于∀x∈K，有 h1(S(x)，S(x0))≤h1(S(x)，Sn(x))+h1(Sn(x)，Sn(x0))+h1(Sn(x0)，S(x0))，且由知，存在N当n＞N时，有，又由 Sn的连续性知，∃的邻域 N()，有，所以由以上知，h(S(x)，1，于是S在K上是连续的。

3)η(·，·)的连续性证明方法与2)相同，只需将测度h2换成‖·‖即可。因ηn(·，x)是仿射的，故ηn(·，αx+b)= αηn(·，x)+ηn(·，b)，两边同时取极限得 η(·，αx+b)=αη(·，x)+η(·，b)，故 η(·，x)也是仿射的。又 ηn(x，x)=0，∀x∈intS(x)，则对于∀x∈intS(x)，存在 { xn}，满足 xn∈intSn(xn)，那么就有ηn(xn，xn)=0。由于，且 ηn连续，故两边取极限得 η(x，x)=0。

由以上1)、2)、3)知，(M，ρ)是完备度量空间。

由于对于任意的u=(S，T，η)∈M，引理1表明GVQVLI有解。记Φ(u)是GVQVLI问题关于u的一个解集，则Φ可以看成从M映到K上的一个集值映射，并且Φ(u)≠0，∀u∈M。

定理2 Φ:M⇒K是usco映射。

证明由于 K是紧集，故只需证 Graph(Φ)是 M×K的闭子集，这里 Graph(Φ)={((S，T，η)，x)∈M ×K:x∈Φ(S，T，η)}。因为M是完备的，K是紧集，故M×K是完备的。所以可证任取序列 {((Sn，Tn，ηn)，xn)}⊂Graph(Φ)满足((Sn，Tn，ηn)，xn)→((S，T，η)，x)∈M ×K。

因为 xn∈ Φ (Sn，Tn，ηn)，则有，xn∈ Sn(xn)且存在 tn∈ Tn(xn)，满足 [ tn，ηn(y，xn)]∉ －intC，∀y∈Sn(xn)。

任取 L(X，Y)中 的 开 集 O⊃ T(x*)，因 为 T(x*)是 紧 集，存 在 ε0＞0使{ξ∈L(X，Y):d(ξ，T(x*))＜ε0}⊂O。由于 ρ((Sn，Tn，ηn)，(S，T，η))→0，xn→x*，T 在 x*点是上半连续的，所 以 ∃N，使 当 n ＞N 时，有且 T(xn)⊂这样，当 n＞N 时，有{ξ∈L(X，Y):d(ξ，T(x*))＜ε0}⊂O。因tn∈Tn(xn)，由引理2知，存在 {tn}的一个子列 { tnp}⊂L(X，Y)，使tnp→t*∈T(x*)，不失一般性，可设tn→t*。

因 xn∈Sn(xn)，ρ((Sn，Tn，ηn)，(S，T，η))→0，xn→x*，且 Sn是连续的因而上半连续的，所以类似地可以证明:存在 { xn}的一个收敛子列 { xnp}，使得 xnp→x0∈S(x*)。由于 xn→x*，可知 x0=x*∈S(x*)。

又由于 S 在 x*下半连续，∀z∈S(x*)，存在 yn∈S(xn)，使得 yn→z。再由 ρ((Sn，Tn，ηn)，(S，T，η))→0 可知∀p∈N，∃np使得取 { xn}的子列 { xnp}，有 h1(Snp(xnp)，S(xnp))＜1/p，于是存在y'np∈Snp(xnp)，使得‖y'np－ynp‖ ＜ 1/p，那么就有‖y'np－z‖≤‖y'np－y'np‖ +‖z－ynp‖ ＜1/p+‖z－ynp‖，而 ynp→z，故有 y'np→z。

又因为 ρ((Sn，Tn，ηn)，(S，T，η))→0，则对于∀(x，y)∈K ×K 有 ηn(x，y)→η(x，y)，且 η 是连续的，则 η(y'np，xnp)→η(z，x*)。所以有 ηn(y'np，xnp)= ［ηn(y'np，xnp)－ η(y'np，xnp)］+［η(y'np，xnp)－η(z，x*)］+ η(z，x*)→η(z，x*)。

又由于之前得到了 y'np∈Snp(xnp)，且 xnp∈Snp(xnp)，tnp∈Tnp(xnp)，所以有

其中Y(－intC)是闭集。对式(1)两边同时取极限得到〈t*，η(z，x*)〉∈Y(－intC)，即〈t*，η(z，x*)〉∉－intC，由 z在 S(x*)中任意性以及 x*∈S(x*)，t*∈T(x*)知 x*∈Φ(S，T，η)，即((S，T，η)，x*)∈Graph(Φ)，从而Graph(Φ)是闭集。由于K是紧集，从而Φ是紧值映射，所以Φ是usco映射。

引理4 如果Φ:M⇒K是usco映射，那么Φ在M的剩余集上是下半连续的。

定义2 对任意u∈M，x∈Φ(u):①称x为u的本质解，若x在K中的任意开邻域O，存在u在M中的开邻域V，使对任意的u'∈V，有Φ(u')∩O≠∅。②称u为本质的，若u的每一个解都是本质的。称u是弱本质的，若存在u的某个解是本质的。

引理5 u为本质的，当且仅当集值映射Φ在u上是下半连续的。

定理3 存在M中的稠密剩余集Q，使对任意的u∈Q，u是本质的。

例1设E=X=Y=(－∞，+∞)，K=［－1，1］，C=R+=x:x≥{}0，考虑如下的GVQVLI:设T(x)={}θ，∀x∈K，其中θ表示零算子;S(x)=K，∀x∈K;η(x，y)=x－y，∀x，y∈K。显然u=(S，T，η)∈M，Φ(u)=K。

构造CVQVLI问题的函数序列 un=(Sn，Tn，ηn)∈M 如下:设 Sn(x)=K，∀x∈K;Tn(x)=易验证 ρ(un，u)→0，〈Tn(x)，ηn(x，y)〉=，所以根据定义2知，u即不是本质的也不是弱本质的。

例1表明，定理3中Q≠M，M中的某些问题元素u所决定的GVQVLI的解集甚至不存在本质解。

3 GVQVLI解集的本质连通区的存在性

在这一部分中设η0:K×K→E取定，满足η0是连续的，固定x∈K，η0(·，x)是仿射的，若x∈intS(x)，则 η0(x，x)=0。令

由例1知，虽然M中有些元素u所决定的GVQVLI不存在本质解，但可以证明，∀u∈M由u所决定的GVQVLI解集至少存在一个本质连通解集，此时，∀u∈M，Φ(u)是K中的紧集。

设u∈M，x∈Φ(u)，Φ(u)中包含x的所有的连通子集的并集称为Φ(u)的一个连通区，Φ(u)的连通区是Φ(u)的连通闭子集，从而是连通的紧子集。Φ(u)中分别包含相异两点的连通区，要么是重合的，要么是不相交的，故Φ(u)被分解为一簇两两不相交的连通区的并集，即Φ(u)有如下的连通区分解:，其中 Λ 为一指标集，对∀α∈Λ，Φα(u)为一非空连通紧子集，且对∀α，β∈Λ，α≠β，有Φα(u)∩Φβ(u)=∅。

定义3 对∀u∈M，设G是其解Φ(u)的非空闭子集，称G为Φ(u)的本质集，若对包含G的K中任意开集O，即存在δ＞0，使得对任意满足ρ(u，u')＜δ的u'，有Φ(u')∩O≠∅。若Φα(u)为Φ(u)的本质集，则称Φα(u)为Φ(u)的本质连通区。Φ(u)的一个本质集G称为极小本质集，若G在Φ(u)的所有本质集的族中按包含关系所定的序关系是极小元。

引理6 设A、B、C是赋范向量空间 E的非空有界凸子集，那么 h(A，λB+μC)≤λh(A，B)+μh(A，C)，其中 h表示的是 Hausdorff距离，λ≥0，μ≥0且 λ +μ=1。

定理4 对任意的u∈M，Φ(u)至少存在一个极小本质集。

证明由定理2知Φ是上半连续的，由上半连续的定义及定义3知Φ(u)本身就是一个本质集。记Ψ为Φ(u)的所有本质集全体，则(按包含关系定序)Ψ非空。对Ψ的任一非空全序子集φ，由于φ的每个成员都是紧的，故φ中所有成员之交仍为紧集，因而φ有下界。于是由Zorn引理可知φ有极小元，这个极小元就是Φ(u)的一个极小本质集。

定理5 对每一个u=(S，T，η0)∈M，Φ(u)的每一个极小本质集都是连通的。

证明设m(u)是Φ(u)的极小本质集，若m(u)不是连通的，则存在Φ(u)的2个非空闭子集c1(u)和 c2(u)以及K 中2 个开集V1、V2，使得m(u)=c1(u)∪c2(u)，c1(u)⊂V1，c2(u)⊂V2，V1∩V2= ∅。由于m(u)是Φ(u)的极小本质集，故c1(u)和c2(u)都不是本质的。于是存在K中开集O1⊃c1(u)，O2⊃c2(u)，使对任意的 δ＞0，存在 u1，u2∈M，从而

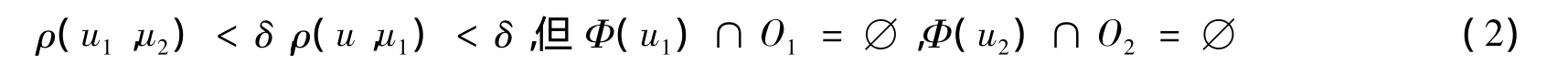
记 W1=V1∩O1，W2=V2∩O2，则 W1、W2都是开集，且满足 W1⊃c1(u)，W2⊃c2(u)，W1∩W2= ∅。因为Φ(u)是紧集，因而 c1(u)和 c2(u)是紧集。故存在 2个开集 U1、U2，使得，其中表示 U1在K 中的闭包。由于U1∪U2⊃m(u)以及 m(u)以及m(u)是本质集，存在 δ'＞0，使对任意满足 ρ(u，u')＜ δ'的 u'，有

又由于 U1⊂O1，U2⊂O2，对 δ'/2 ＞0，由式(2)知存在 u1，u2∈M，使得

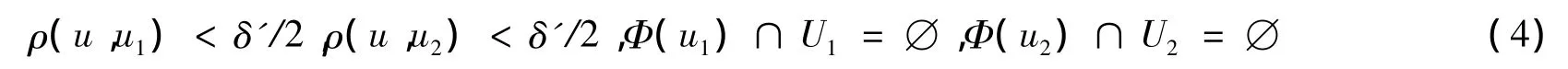
记 u1=(S1，T1，η0)，u2=(S2，T2，η0)，现构造一个 u'=(S'，T'，η0)如下:

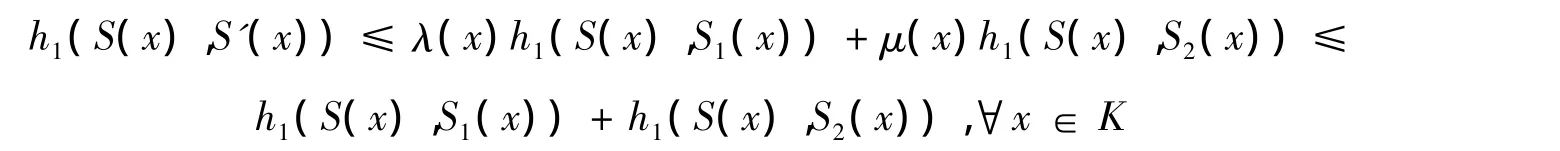
且

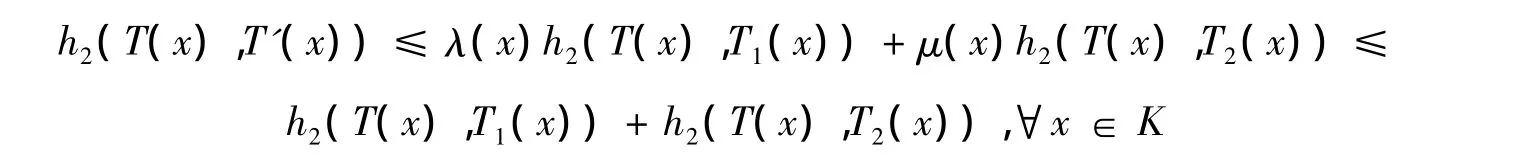
所以，根据式(4)有

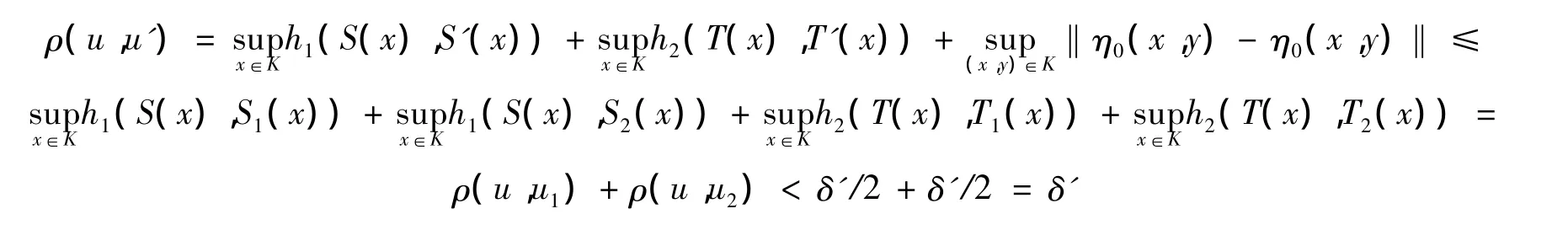
再由式(3)得

但是由 u'的构造又有如下事实:设 x∈U1，则当 λ(x)=1，μ(x)=0时，有 S'(x)=S1(x)，T'(x)=T1(x);若 x∈Φ(u')，则 x∈S'(x)=S1(x)，且存在 t∈T'(x)=T1(x)，使得〈t，η0(y，x)〉∉ － intC，对于任意的y∈S'(x)=S1(x)。于是x∈Φ(u1)，这与式(4)矛盾。故Φ(u')∩U1=∅。同理可证Φ(u')∩U2=∅。所以Φ(u')∩(U1∪U2)=∅，这与式(5)矛盾，因此m(u)必是连通的。

定理6 对每一u∈M，Φ(u)中至少存在一个本质连通区。

证明由定理4、5知，Φ(u)中至少存在一个连通的极小本质集G，而G必包含于Φ(u)的连通区Φα(u)，因为G是本质的，由定义可知Φα(u)就是Φ(u)的本质连通区。

定理7 若u∈M使得Φ(u)仅由孤立点组成，则u是弱本质的，特别的，若Φ(u)是单点集，则u必是本质的。

4 本质连通区的连续性

已知(M，ρ)是一个可测空间，而(K，d)是紧的可测空间。对于任意的 ε＞0，x∈K，A⊂M，记O(x，ε)= {u∈M:ρ(x，u)＜ε }，U(ε，A)= {y∈K:∃u∈A，使得 d(u，y)＜ ε}，B(ε，A)={y∈K:∃u∈A，使得 d(u，y)≤ε}。显然，U(ε，A)是开集，而当A是紧集时B(ε，A)是闭集。

定理8 对于任意的u∈M，如果m(u)是Φ(u)的最小本质集，那么对于任意的ε＞0，∃δ＞0，使得对于任意 u'∈M，若满足 ρ(u，u')＜δ，则存在 Φ(u')的最小本质集 m(u')，并且有m(u')⊂B(ε，m(u))。

证明假设结论不成立，即存在ε0＞0，使得对任意的δ＞0，都存在u'∈M，ρ(u，u')＜δ满足m(u')⊄B(ε0，m(u))，其中m(u')是Φ(u')中任意的最小本质集。

由于m(u)是 Φ(u)的本质集，则对以上的 ε0＞0，存在 δ0＞0，使得对任意的 u'∈M 且 ρ(u，u')＜ δ，有 U(ε0，m(u))∩Φ(u')≠∅。

又因为 B(ε0，m(u))∩Φ(u')是 Φ(u')中的闭子集并且 B(ε0，m(u))∩Φ(u')⊂B(ε0，m(u))，再由假设知 m(u')⊄B(ε0，m(u))，所以 B(ε0，m(u))∩Φ(u')不是 Φ(u')的本质集。那么，存在 ε1＞0，使得对于任意的 δ＞0，存在 u″∈M，ρ(u'，u″)＜δ，但是 U(ε1，B(ε0，m(u))∩Φ(u'))∩Φ(u″)=∅。

令 δ1，δ2，δ3，…是单调下降趋向于 0 的序列，使得 O(u'，δn)⊂O(u，δ0)。再取 un∈O(u'，δn)，满足U(ε1，B(ε0，m(u))∩Φ(u'))∩Φ(un)=∅。由于 ρ(u，un)＜ δ0，U(ε0，m(u))∩Φ(un)≠∅，再令 yn∈U(ε0，m(u))∩Φ(un)，因为 K 是紧集，所以不失一般性，假设 yn→y0∈B(ε0，m(u))。又因为 xn→x'，yn∈Φ(xn)，yn→y0，且 Φ 是 usco 的，所以就有 y0∈Φ(u')。然而，yn∈Φ(un)，U(ε1，B(ε0，m(u))∩Φ(u'))∩Φ(un)=∅，所以就有 yn∉U(ε1，B(ε0，m(u))∩Φ(u'))。再由 yn→y0，就可以得到 y0∉U(ε1/2，B(ε0，m(u))∩Φ(u'))，这与 y0∈B(ε0，m(u))∩Φ(u')矛盾。所以结论成立。

定理9 对于任意的u∈M，如果c(u)是Φ(u)的最小本质区，并且存在ε0＞0，使得B(ε0，c(u))∩B(ε0，Φ(u)c(u))=∅，那么对任意的 ε ＞0，∃δ＞0，使得对于任意 u'∈M，若满足 ρ(u，u')＜ δ，则存在Φ(u')的最小本质区c(u')，并且有c(u')⊂B(ε，c(u))。

证明首先，存在Φ(u)的最小本质集m(u)，满足m(u)⊂c(u)。再根据定理8，∀ε＞0，∃δ1＞0，使得∀u'∈M，ρ(u，u')＜δ1，存在 Φ(u')的最小本质集 m(u')，满足 m(u')⊂B(ε，m(u)⊂B(ε，c(u))。又有Φ(u')的一个区c(u')，满足m(u')⊂c(u')，所以显然c(u')是Φ(u')的一个本质区。

Φ在u处是上半连续的，所以存在 δ2＞0，使得对于任意的 u'∈M，ρ(u，u')＜δ2，有 Φ(u')⊂U(ε，Φ(u))⊂B(ε，c(u))∪B(ε，Φ(u)c(u))。下证 Φ(u)c(u)是闭集，故也是紧的。对于∀yn∈Φ(u)c(u)，yn→y，有 yn∈Φ(u)，yn∉c(u)。由于 Φ(u)是紧的，有 y∈Φ(u)。如果 y∈c(u)，则对于足够大的 n，yn∈B(ε0，c(u))成立，但是这与 B(ε0，c(u))∩B(ε0，Φ(u)c(u))= ∅矛盾，因此 y∉c(u)，y∈Φ(u)c(u)，所以，Φ(u)c(u)是闭集因而是紧的。

令 δ=min{ δ1，δ2}，对于∀u'∈M，ρ(u，u')＜ δ，若 c(u')⊄B(ε，c(u))，那么 c(u')∩B(ε，Φ(u)c(u))≠∅且 c(u')∩B(ε，Φ(u))≠φ(因为 m(u')是它们的子集)。注意到当 ε ＜ε0时，B(ε，c(u))∩B(ε，Φ(u)c(u))=∅。由于 c(u)和 Φ(u)c(u)都是紧的，所以 B(ε，c(u))和 B(ε，Φ(u)c(u))都是闭集。也就是非空连通集c(u')与2个非空闭集相交，不可能成立。因此就有结论c(u')⊂B(ε，c(u))。

备注2 如果Φ(u)是连通的，即Φ(u)的唯一本质区就是它自己，那么由于Φ是上半连续的，则对于∀ε＞0，∃δ＞0，使得∀u'∈M，ρ(u，u')＜ δ，有，因此，对于 Φ(u')的任一本质区 c(u')，有 c(u')⊂Φ(u')⊂B(ε，Φ(u))成立。

［1］Fort M K.Essential and nonessential fixed points［J］.Am J Math，1950，72:315 －322.

［2］Kinoshita S.On essential components of the set of fixed points［J］.Osaka J Math，1952，4:19 －22.

［3］Wu W J，Jiang J H.Essential equilibrium points of n-person non-cooperative games［J］.Sci Sinica，1962，11:1307 －1322.

［4］Jiang J H.Essential components of the set of fixed points of the multivalued mappings and its applications to the theory of games［J］.Sci Sinica，1963，12:951 －964.

［5］Kohlberg E，Mertens J F.On the strategic stability of equilibria［J］.Econometrica，1963，54:1003 －1037.

［6］Hillas J.On the definition of the strategic stability of equilibria［J］.Econometrica，1990，58:1365 －1390.

［7］Yu J，Luo Qun.On Essential Components of the Solution Set of Generalized Games［J］.J Math Anal And Appl，1999，230:303－310.

［8］罗群，邓晓红，孙天翔.广义向量似变分不等式解集的通有稳定性及本质连通区的存在性［J］.系统科学与数学，2002，22(1):90－95.

［9］Chen J C，Gong X H.The Stability of Set of Solutions for Symmetric Vector Quasi-Equilibrium Problems［J］.J Optim Theory Appl，2008，136:359 －374.