某汽车差速器齿轮的强度分析及疲劳寿命预测

王良模，刘 飞，夏汉关，赵红军，王小乾，张艳伟

(1.南京理工大学 机械工程学院，南京 210094;2.江苏太平洋齿轮传动有限公司，江苏姜堰 225500)

差速器是汽车传动系的重要总成，而差速器齿轮又是差速器的关键零件，它的可靠性直接影响汽车整车的质量。但差速器作为汽车零部件中一个较小的总成，只有部分学者对它单独进行了设计、分析。蒋法国等［1］分析了差速器行星齿轮弯曲强度，得出随着齿根圆角半径的增大齿根应力逐渐减小的结论;李维国等［2］运用ABAQUS作为求解器，对差速器齿轮进行强度校核;郑慧林［3］基于有限元法进行了微型车驱动桥结构分析及疲劳寿命预测研究;ANDREWS J D［4］利用有限元法进行了齿轮应力的分析并通过光弹性试验进行了验证;H.Von Eiff等［5］研究了齿形对齿轮应力的影响。本文基于有限元技术和疲劳寿命方法，进行了差速器齿轮强度分析及疲劳寿命预测。

1 差速器齿轮的有限元分析

随着齿轮精锻技术的发展，轿车差速器齿轮大量采用精锻工艺。相对于传统齿轮，精锻齿轮的尺寸更小、强度更高，所以传统齿轮设计中采用的设计及校核方法显得相对保守。为了更准确地对齿轮进行几何设计和强度分析，使用先进的CAE工具对齿轮进行相关参数设计和强度分析显得愈加重要。

对于汽车差速器锥齿轮副来说，在大多数情况下，汽车左右轮是等速或接近等速的，行星齿轮和半轴齿轮相对接近静止，因此，行星齿轮经常只是起等臂推力杆的作用，弯曲强度应为主要考虑因素。

1.1 差速器齿轮有限元模型的建立

基于CAD/CAE一体化技术，本研究有限元软件选用ANSYS 11.0。该软件和UG软件可无缝连接，在 UG的主菜单中添加了 ANSYS 11.0菜单项。

在UG中生成齿轮三维模型后，直接点击ANSYS 11.0菜单项，进入 ANSYS 11.0界面，然后选择单元类型、单元尺寸、材料属性等［6］。所建差速器行星齿轮、半轴齿轮的有限元模型如图1所示。

图1中2个齿轮为常规结构。

图1 齿轮有限元模型

1.2 差速器齿轮弯曲强度分析［7］

齿轮加载方法有2种:

1)在齿轮轮毂加载等效力矩，此时位移的约束需施加在齿顶部位;

2)将齿轮所承受的转矩转化为单齿啮合最高点所承受的线性分布力。

本文所研究的差速器行星齿轮的加载方式选择后者。

载荷沿齿面接触线的分布是决定齿轮应力的基础，因此，精确确定载荷沿齿面接触线的分布状态，对于齿轮强度分析具有十分重要的意义。锥齿轮承受的转矩转化到单齿最高啮合线上的载荷不是均匀分布的。直齿锥齿轮齿面接触线载荷自大端逐渐向小端减小，但并不是呈精确的线性关系，而是略呈抛物状。在接近两端处，接触线载荷急剧下降，这是边界效应所致(一般锻造齿轮通过齿面修形可避免边界效应)，但是影响范围不大。在接触中间段载荷分布比较均匀，虽非直线分布，但在进行计算时可以近似作线性载荷处理，不会带来较大误差。锥齿轮的受力如图2所示。

本文所分析的齿轮是对称零件，因此，建立了行星齿轮和半轴齿轮单齿的有限元模型来进行分析。其中行星齿轮单齿有限元模型共有2982个节点、2211个实体单元;半轴齿轮单齿有限元模型共有2414个节点、1659个实体单元。齿轮单齿有限元模型如图3所示。

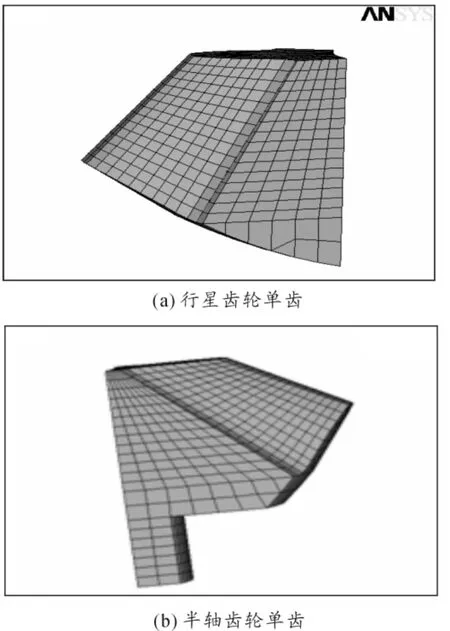
图3 齿轮单齿有限元模型

约束行星齿轮内圈的所有自由度，将圆周力F1=3.52 ×104N、径向力 F2=1.36 ×104N、轴向力F3=9.1×103N近似作线性载荷处理，按照比例施加在单齿啮合的最高点处。计算所得有限元结果如图4所示。

由图4可得:行星齿轮单齿最大弯曲应力为1697 MPa，出现在齿根处，符合行星锥齿轮的破坏多出现在齿根的实际情况。

图4 行星齿轮单齿弯曲应力云图

用同样的求解方法可以得到半轴齿轮的有限元计算结果，如图5所示。

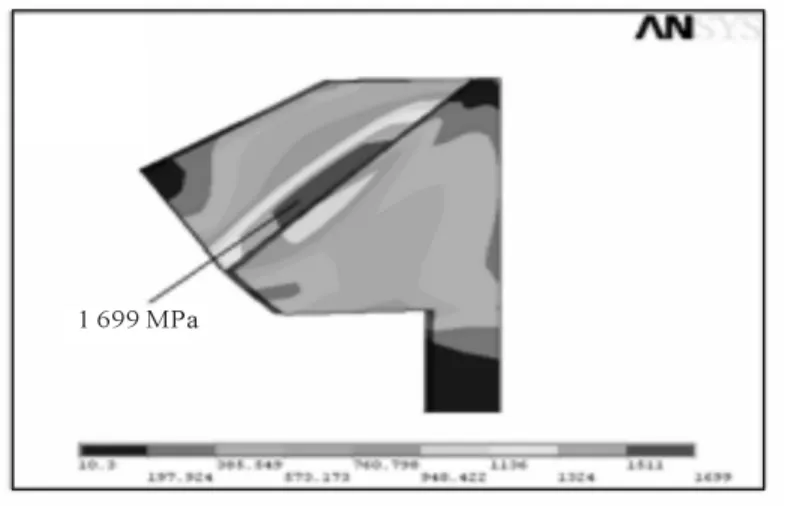
图5 半轴齿轮单齿弯曲应力云图

由图5可得:半轴齿轮单齿最大弯曲应力为1699 MPa，出现在齿根处，符合半轴齿轮破坏多出现在齿根的实际情况。

2 齿轮的疲劳分析

由于本课题所研究的差速器齿轮是需要承受疲劳载荷的结构，且最大应力都未达到屈服极限，因此，本研究选择了简单实用且成熟的总寿命分析法对齿轮的疲劳寿命进行分析。

MSC.Fatigue提供了友好的用户界面以及广泛的输入、输出接口，可以同其他有限元分析软件(如ANSYS)以及CAD软件(如AutoCAD)进行数据交换［8］。

本研究主要是在进行完ANSYS的静力分析的基础上进行疲劳分析，其计算结果信息保存在*.rst文件中。打开MSC.Fatigue疲劳分析软件，调入ANSYS对齿轮的静力分析结果文件*.rst。

齿轮的材料是20CrMnTi，通过查阅相关材料性能手册获取S－N曲线。

齿轮的疲劳载荷:本研究选择了简单的正弦载荷作为齿轮所承受的疲劳载荷，利用齿轮齿根弯曲的应力分析结果进行疲劳分析，所以，疲劳载荷曲线的纵坐标相当于一个比例系数，其最大值取1，最小值取0，周期为0.31 s，即疲劳载荷的最大值为实际的最大载荷，最小值为0。

利用齿轮单齿的齿根弯曲强度的应力结果以及相应的疲劳载荷和材料S－N曲线，即可计算出存活率为50%时齿轮的疲劳寿命。

图6为行星齿轮的单齿疲劳寿命云图，可以看出，行星齿轮齿根区域是应力最大的地方，同时也是寿命最低的部位，因此，疲劳寿命最低的位置基本保持在应力最大的部位。由图6还可以看出最低寿命为4.86E4次循环，超过这个循环数时行星齿轮就有可能发生破坏。

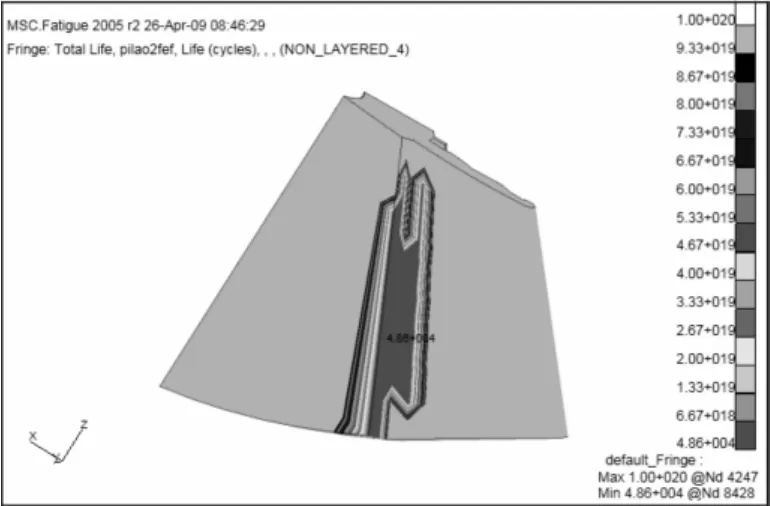
图6 行星齿轮的单齿疲劳寿命云图

图7为半轴齿轮的单齿疲劳寿命云图，从图中可看出，半轴齿轮的最低疲劳寿命的位置保持在应力最大的部位，最低寿命为3.55E4次循环，超过这个循环数时半轴齿轮就有可能发生破坏。同时由于差速器齿轮并不是随时随刻工作，只有左右车轮出现转速差时它才起作用，因此，本设计齿轮的寿命满足要求。

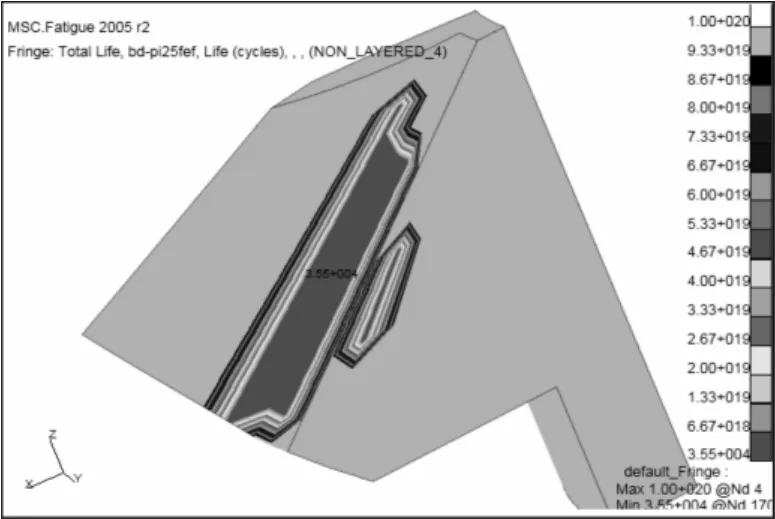
图7 半轴齿轮的单齿疲劳寿命云图

3 结束语

利用有限元分析软件ANSYS对差速器半轴锥齿轮和行星齿轮进行静强度分析，分析结果表明弯曲强度在许用强度之内，符合强度要求。对锥齿轮进行了简单的全寿命分析，利用差速器齿轮齿根弯曲有限元的结果进一步在MSC.Fatigue中分析，得到齿轮单齿的疲劳寿命。从计算结果可知，齿轮的疲劳寿命满足设计要求。由于差速器齿轮是差速器的核心零件，对其进行CAE分析具有重要意义。

［1］蒋法国.差速器行星齿轮的有限元法强度分析［D］.长春:吉林大学，2006.

［2］李维国，李剑敏.差速器齿轮有限元精确建模与强度分析［J］.机械传动，2011，35(12):70 －72.

［3］郑慧林.基于有限元法的微型车驱动桥结构分析及疲劳寿命预测研究［D］.南京:南京理工大学，2008.

［4］ANDREWS J D.A finite element analysis of bending stresses induced in external and internal involutes spur gears［J］.Journal of Strain Analysis，1991，26(3):153－163.

［5］Von Eiff H.Influence of Gear Tooth Geometry on Tooth stress of External and Internal Gears［J］.Trans ASME J mech，1990，112:575 －583.

［6］刘惟信.圆锥齿轮与双曲面齿轮传动［M］.北京:人民交通出版社，1980.

［7］张朝晖.ANSYS11.0结构分析工程应用实例解析［M］.北京:机械工业出版社，2008:120－223.

［8］周传月，郑红霞，罗慧强，等.MSC.Fatigue疲劳分析用用与实例［M］.北京:科学出版社，2005:8－158.